Dissection and Tesselation

List of animations posted on this page.(Click the text to watch animation.)
Use browser's "Back" button to come back to this page.

See Triangle to Square in animation

Go to Triangle to Square

See triangle to square model in animation

Go to Triangle to Square

See Rectangle to Square in animation

Go to Rectangle to Square

See Square to Octagon in animation

Go to Square to Octagon

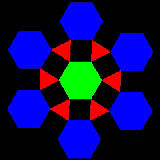
See Hinged Tesselation #1 in animation

Go to Hinged Tesselation

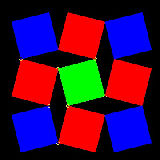
See Hinged Tesselation #2 in animation

Go to Hinged Tesselation

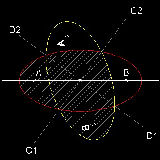
See Ellipse to Heart - 2d illustration in animation

Go to Ellipse to Heart - 3D Rotation

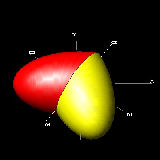
See Ellipse to Heart in animation

Go to Ellipse to Heart - 3D Rotation

See Pythagorean numbers in animation

Go to Pythagorean Tesselation

See Drawing cycloid curve in animation

Go to Area under cycloid

See Area under cycloidal arch- Octagon case in animation

Go to Area under cycloid

See Kürschák's Tile in animation

Go to Kürschák's Tile

See Square within square in animation

Go to Square with (1/n) area within a square

See Origami square within square in animation

Go to Square with (1/n) area within a square

See Origami - (1/3) square within square in animation

Go to Square with (1/n) area within a square

See Example of reptiles - Sphinx in animation

Go to Reptiles

Transformation
Pythagorean Tesselation
Area under cycloid
Kürschák's Tile
Square with (1/n) area within a square
Reptiles
Dudeney's Circle Quizzes
Sam Loyd's Red Spade Quiz

1. Transformation

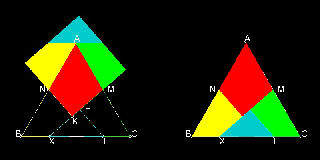
1.1 Triangle to Square

This is one of the most famous dissection by Henry E. Dudeney.(Ref. 2,3,4,5,6).

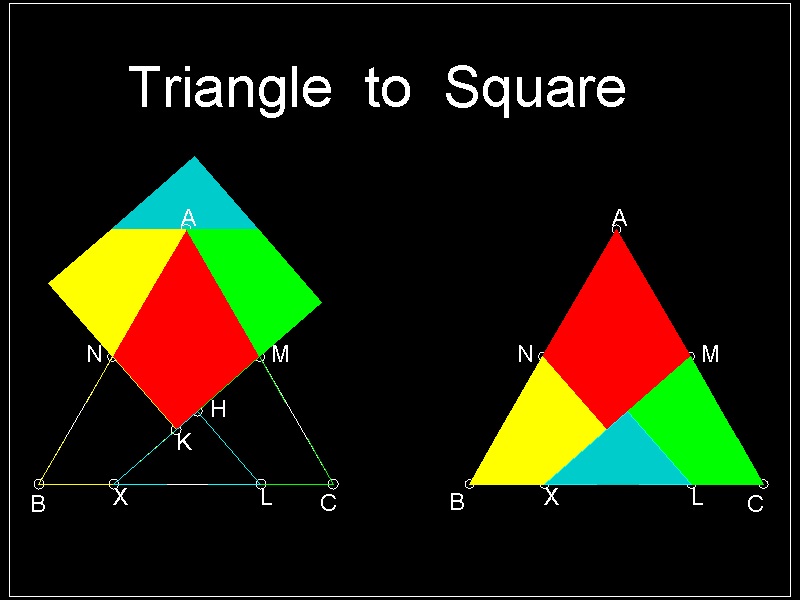**************************** tr_2_sqr.dwg *********************************
You can see the process in animation.

To create this drawing and animation:
Load dissect_tessel.lsp (load "dissect_tessel")
Then from command line, type tr_2_sqr

How to find the coordinates of all points used in this dissection

Ref. 3 explains a standard procedure used in finding the dissection from one geometric shape to another like a case here: from equilateral triangle to square.

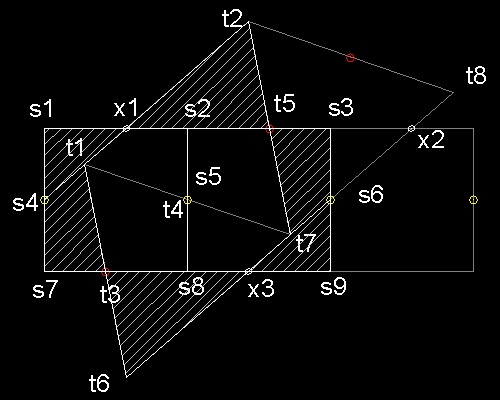
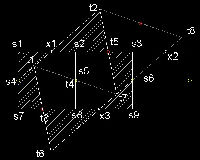
*********************** tr_2_sqr_model.dwg *********************
(1) arrange triangles and squares horizontally.
(2) move the group of triangles such tha mid points t4 and s5 coincide and t3 falls on the line s7-s8.

The location of this point can be computed by
Pythagorean theorem : (t3 - s8)² = (t3 - t4)² - (s5 - s8)²

You can see the process in animation.

To create this drawing and animation:
Load dissect_tessel.lsp (load "dissect_tessel")
Then from command line, type model_analysis
Additional editing (hatching & texts) is required.

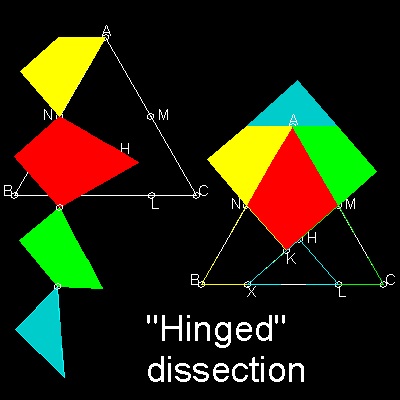
Hinged version

Ref.5 is a very interesting book on hinged dissections.
"Triangle to Square" dissection in this section is the first example discussed in the book.

************* hinged_tr2sqr.dwg *************

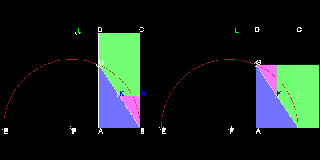
1.2 Rectangle to Square

************************************* rec_2_sqr.dwg *************************************

You can see the process in animation.

To create this drawing and animation:
Load rec_2_sqr.lsp (load "rec_2_sqr")
Then from command line, type rec_2_sqr

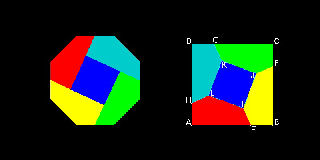
1.3 Square to Octagon

This is one of the H.E.Dudeney's masterpiece.

************************************** sqr_2_oct.dwg **************************************

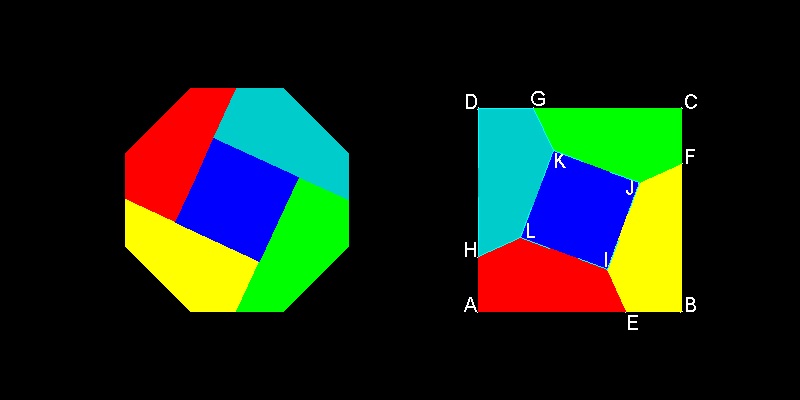
You can see the process in animation.

To create this drawing and animation:
Load sqr_2_oct.lsp (load "sqr_2_oct")
Then from command line, type sqr_2_oct

How to find the coordinates of all points used in this dissection

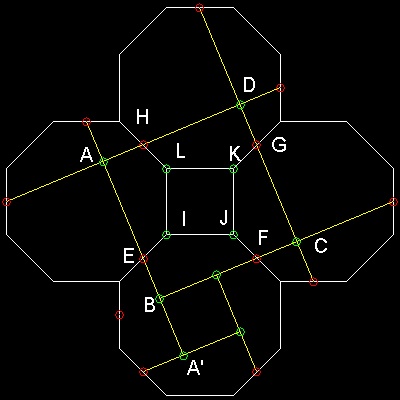
All the red colored points are the mid-point of octagon's sides.
The green colored points are intersections of the line connecting these red points.
************* sqr2oct_model.dwg *************

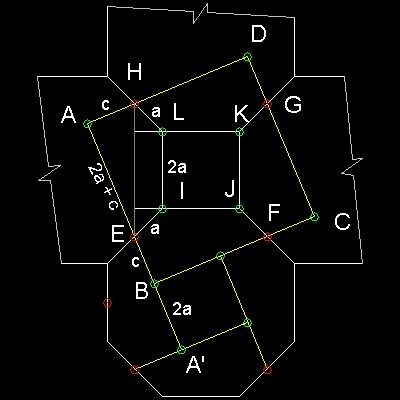
Let the length of octagon side be 2a.

Then,because angle HLK = 135 degrees,

HL = EI = a , HE = 2a + sqrt(2) a

Let AH = c, then AE = 2a + c

Using the relation AH² + AE² = HE²,

length of c can be calculated.
********** sqr2oct_model_detail.dwg **********

1.4 Greek Cross

The Greek cross which is composed of five unit squares,where
five is the sum of two squares: 5 = 2² + 1².
Its tesselation is done in a very simple manner.

H.E.Dudeney presented the following puzzle:
To cut a Greek cross into 4 or 5 pieces,which can be rearranged to form a square.
Three solutions are shown in 3 different colors.
Thick lines are the cutting lines, and 4 or 5 pieces form squares .

************************************ Greek_cross.dwg ************************************

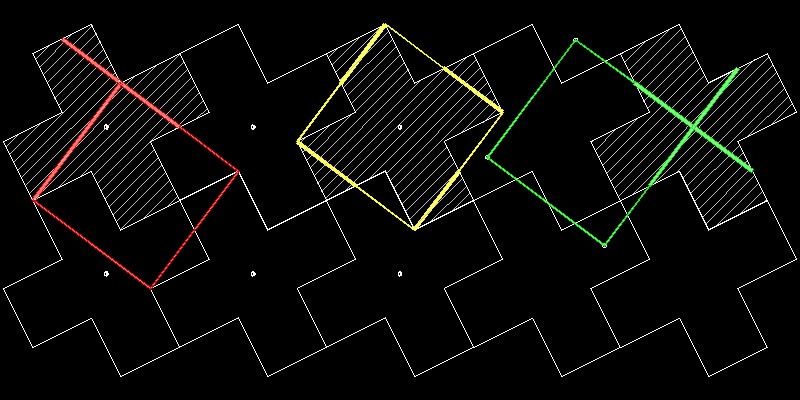
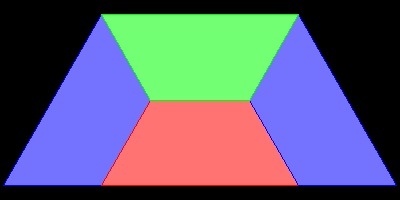
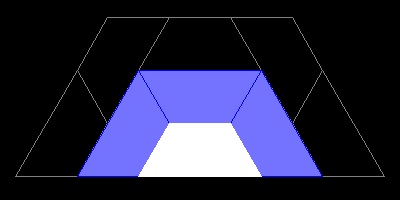
1.5 Hinged Tesselation

David Wells (Ref.6) shows two interesting samples of "Hinged Tesselation".

You can see the process in animation.

To create this drawing and animation:
Load tessel_1.lsp (load "tessel_1")
Then from command line, type auto_play

**************** hinge_1.dwg ****************

You can see the process in animation.

To create this drawing and animation:
Load tessel_2.lsp (load "tessel_2")
Then from command line, type auto_play

**************** hinge_2.dwg ****************

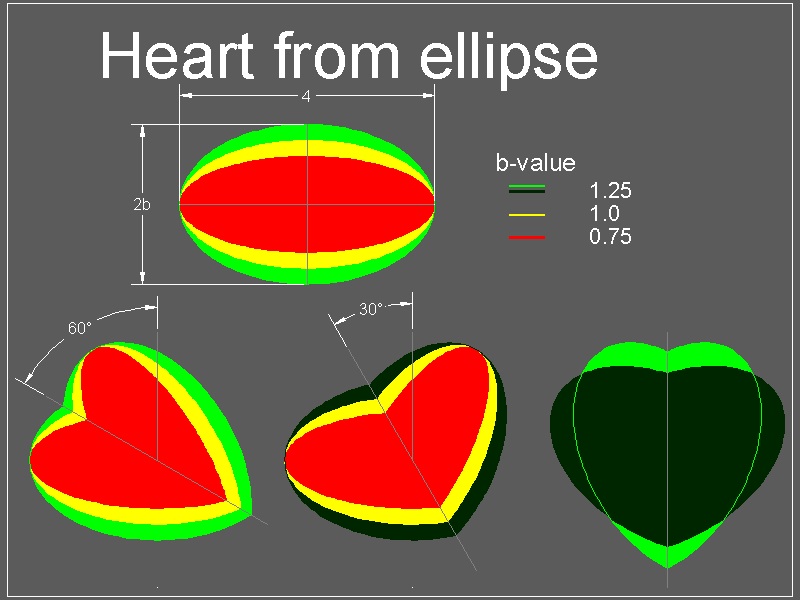
1.6 Ellipse to Heart - 3D Rotation

This is a very simple , and yet, interesting example of 3D rotation (or twist).(Ref-5)
In 1985 , William Esser III was granted a US patent for his idea of making a heart shape from rotating half of the ellipsoid.
His idea is illustrated in 2D drawing.

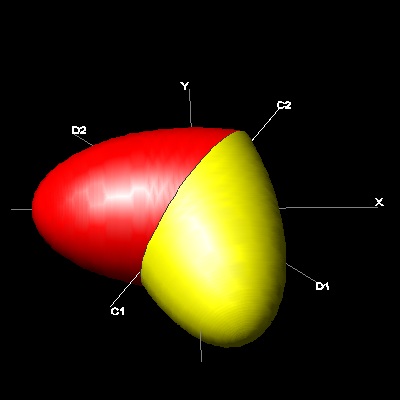
An ellipse is cut in half by a line C1-C2 passing through its center.
Draw line passing through the center perpendicular to C1-C2.
This ellipse (in red) are rotated 180 degrees out of plane around the axis D1-D2.
The result is another ellipse in color yellow.
Combining red & yellow ellipses, we have two "heart shaped" regions.

You can see the process in animation.

To create this drawing and animation:
Load ellipse_2_heart.lsp (load "ellipse_2_heart")
Then from command line, type ellipse_2_heart_2d
*********** ellipse_2_heart_2d.dwg ***********

3 dimensional case

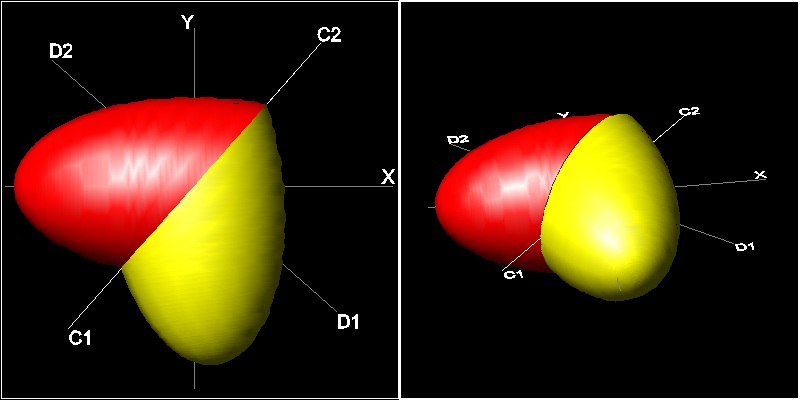
******************************** ellipse_2_heart_2views.dwg ******************************

This is the case when the same process is applied to the ellipsoid.

An ellipsoid is created when an ellipse is rotated a full 360 degrees
about the axis (in this case , major axis).

You can see the process in animation.

To create this drawing and animation:
Load ellipse_2_heart.lsp (load "ellipse_2_heart")
Then from command line, type multi_view

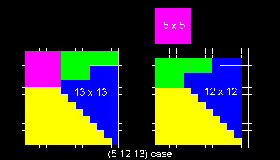
2. Pythagorean Tesselation (Ref 4)

Let x, y and z be the side length of the squares.
Diophantus , a fourth-century Greek mathematician from Alexandria, found a method
to generate all basic solutions to x² + y² = z².
His solution was stated later by the 7-th century Indian mathematician Brahmagupta as follows:
Every basic solution is of the form
x = m² - n², y = 2mn , z = m² + n²
where m and n are relatively prime and m + n is odd.
According to Ref.4, there are two classes of solutions.
The first one is called Pythagoras class,for which m = n + 1.
This incluses cases like (3 4 5), (5 12 13),(7 24 25),etc
The second is called Plato class,for which n = 1 in Diophantus's method.
The first three solutions in this class are (3 4 5), (15 8 17), and (35 12 37).
Only the first class is treated here now. The second class will be added in the future.

****************************** 5_12_13_case.dwg ******************************

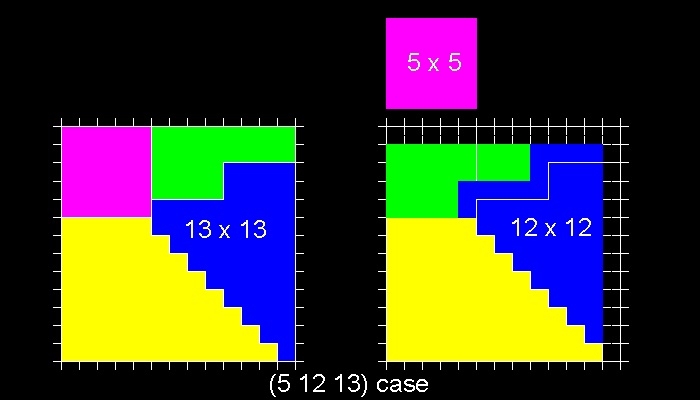
You can see the process in animation.

To create this drawing and animation:
Load tessel_pclass.lsp (load "tessel_pclass")
Then from command line, type tessel_pclass
To see (5 12 13) case, input 2.

More examples

************** 3_4_5_case.dwg ************** ************** 7_24_25_case.dwg *************

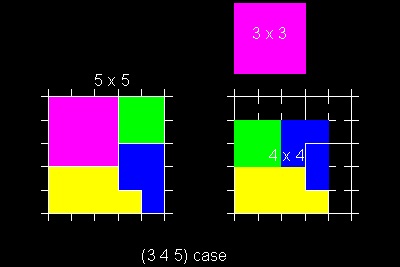
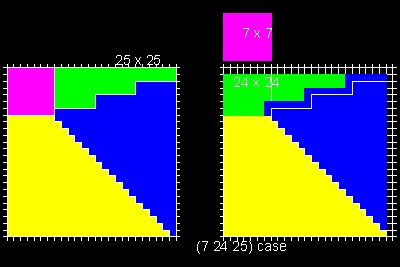
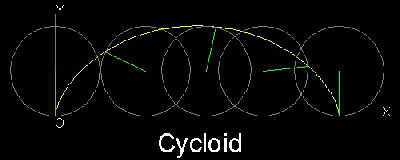
3. Area under cycloid (Ref 7,11)

The cycloid is the path of a point of a circle rolling upon a fixed line.
Its parametric equation is : x = a(θ - sinθ) , y = a(1 - cosθ)
where a is a radius of the rolling circle, and θ is an angle (in radian).

You can see the process in animation.

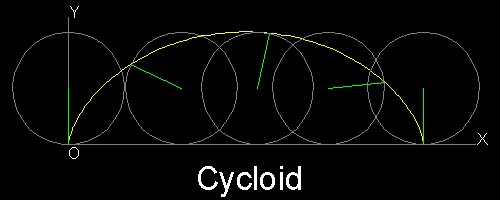
To create this drawing and animation:
Load cycloid1.lsp (load "cycloid1")
Then from command line, type cycloid_curve
********************* cycloid_1.dwg *********************

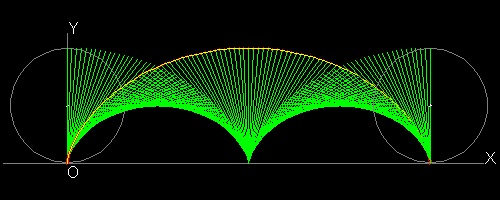
To create this drawing:
By drawing diameters instead of radii,a very interesting curve shows up.
Two cycloids are created by a series of lines.
This is one of the popular subjects in string art called "Curve Stitching".(Ref.12)
********************* cycloid_2.dwg *********************

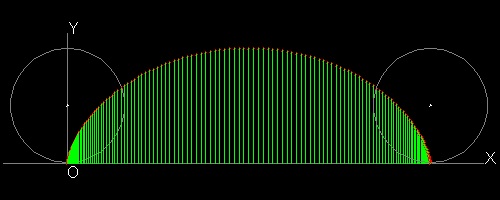
Rough estimate of area under the curve.
The area under the curve is the summation of all the areas of tiny rectangles.
In the case when angle increment = (2π) / 150, estimated area is 9.423859.
Divided by 3, this gives π = 3.1413
To excute the program, type cycloid_area. The result will show up in the text window.
********************* cycloid_3.dwg *********************

Visual demonstration using regular polygons

(Ref. 10) In 1599, Galileo Galilei tried to find the area under a cycloidal arch by comparing the weights of the generating circle and a cycloidal arch made of the same material. He conjectured that the area sought is about 3 times the generating circle, but he thought the ratio must be some irrational number and gave up his experiment.

Galileo Galilei is the person who gave the name "cycloid".
The proof that his guess was actually correct (exactly 3 times) was given by Roberval in 1634.

****************************** cycloid_area_8.dwg ******************************

You can see the process in animation.

To create this drawing and animation:
Load cycloid_area.lsp (load "cycloid_area")
Then from command line, type cycloid_area
To see octagon case shown here, input 8.

More examples

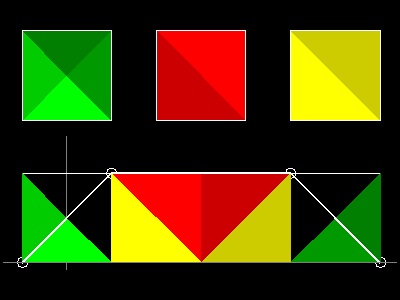
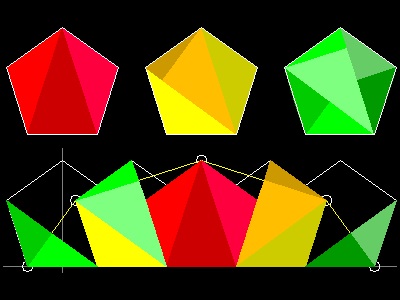
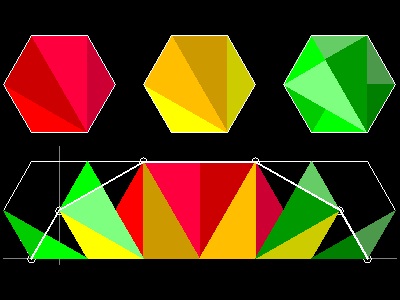
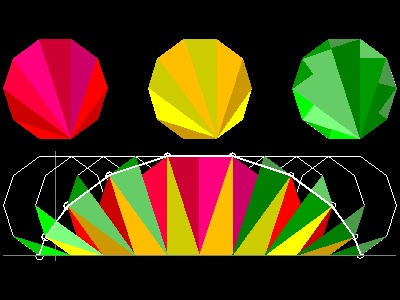
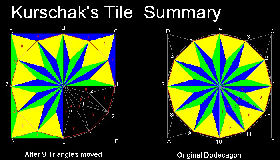
************* cycloid_area_4.dwg ************ ************** cycloid_area_5.dwg ************

************* cycloid_area_6.dwg ************ ************** cycloid_area_10.dwg ***********

4. Kürschák's Tile (Ref. 6,7,13)

Kürschák's Theorem:

The area of a regular dodecagon (12) inscribed in a circle of unit radius is 3.

****************************** Kurschak_tile.dwg ******************************

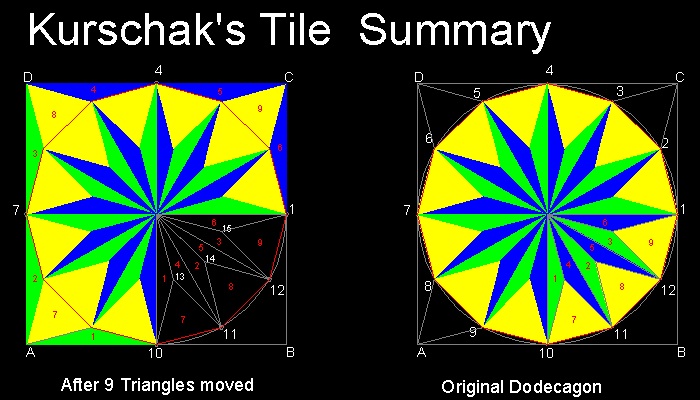
You can see the process in animation.

To create this drawing and animation:
Load Kurschak.lsp (load "Kurschak")
Then from command line, type Kurschak

How to draw a dodecagon

************ draw_dodecagon.dwg ************

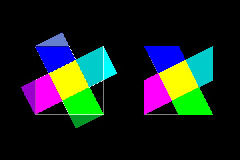
5. Square with (1/n) area within a square (Ref 7,9)

This is one of the well-known Dudeney's puzzle:

To cut a Greek cross into 5 pieces which can be rearranged to form a square.
This dissection was used as a visual proof that the area of the yellow square
is 1/5 of the outside square.(Ref. 7)

************************** sqr_within.dwg **************************

You can see the process in animation.

To create this drawing and animation:
Load sqr_within.lsp (load "sqr_within")
Then from command line, type sqr_within

H.Abe's Origami solution and generalization for any (1/N)

It is a very simple origami exercise to make (1/5) area square within a square.
In the drawing below, E,F,G,H are the mid points of the side.
By folding a square paper along the 4 lines AE,BF,CG & DH, the resulting square
in the center is the solution.

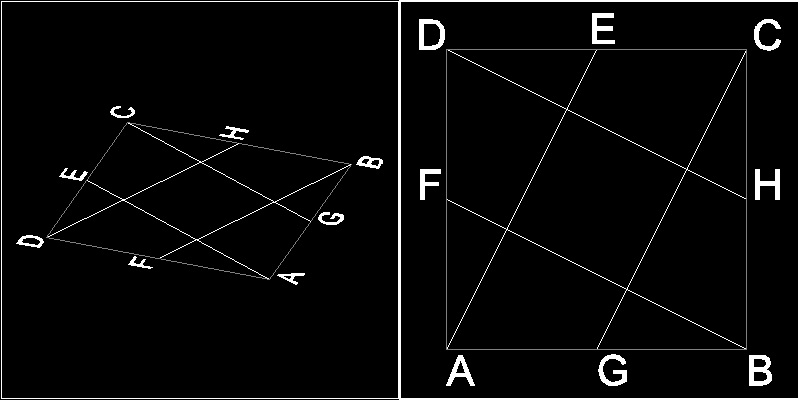
********************************* origami_sqr_within.dwg *********************************

You can see the process in animation.

To create this drawing and animation:
Load sqr_within.lsp (load "sqr_within")
Then from command line, type origami_sqr_within

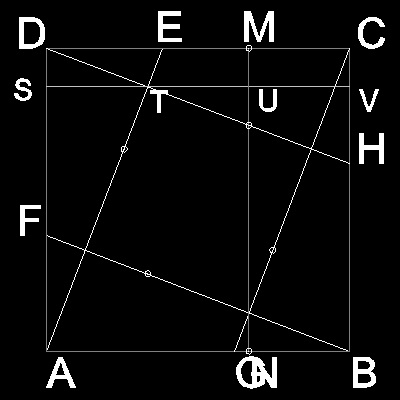
But Hisashi Abe noticed that the line MN, which goes through point P, and parallel to AD
is located at (1/5) of the distance AB from line BC. or , MC = NB = (1/5) AB
Then he came up with an alternative and general method to make a (1 / n) square as follows:
(1) mark MN at a distance (1/n) from edge BC
(2) move D onto line MN using A as a pivot,then mark crease line AE
(3) move A onto line AE using B as a pivot,then makr crease line BF
....simlar operation for B & C
Then crease lines AE,BF,CG & DH enclose a square ,area of which is (1/n) of the square paper.
Example is for n = 3 case.

************* sqr_within_fifth.dwg ************ ************* one_third_case.dwg ************

You can see the process in animation.

To create this drawing and animation:
Load sqr_within.lsp (load "sqr_within")
Then from command line, type abe_sqr_within
Then input N=3

Proof

Since ST = TU = (1/2)(1-UV) , area of triangle DAT = (1/2)DA x ST = (1/4)(1 - UV).
Area of inside square = ABCD - 4 (area of DAT) = 1 - (1 - UV) = UV
This means that UV does not have to be (1/N), but any number between 0 and 1.

So this H.Abe's origami method can be stated as follows:
"MN is parallel to DA. Then the area of inside square is equal to the ratio MC/DC."

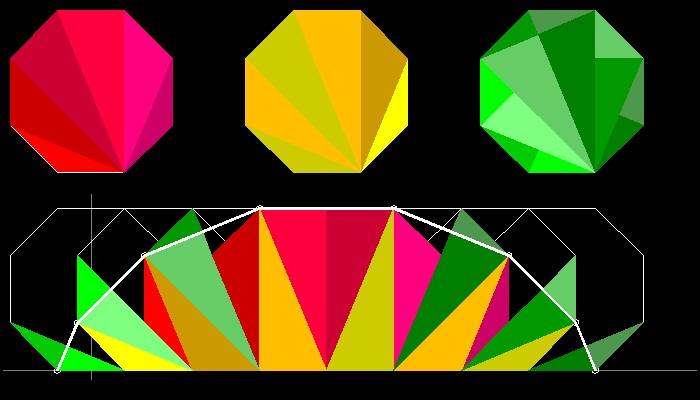
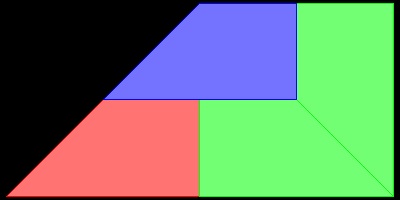
6. Reptiles (Ref 8)

In 1940, C.D.Langford published a paper on "repetitive tile" (hence named "reptiles") (ref.9).
Ref.1 lists the following 11 polygons,which can be dissected into identical copies of themselves.
They are

4 trapeziums
4 L - shapes
pentagon called "sphinx", isosceles right-angled triangle, any parallelogram with sides in the ratio of 1 and √2.

************************* reptiles_table.dwg ************************

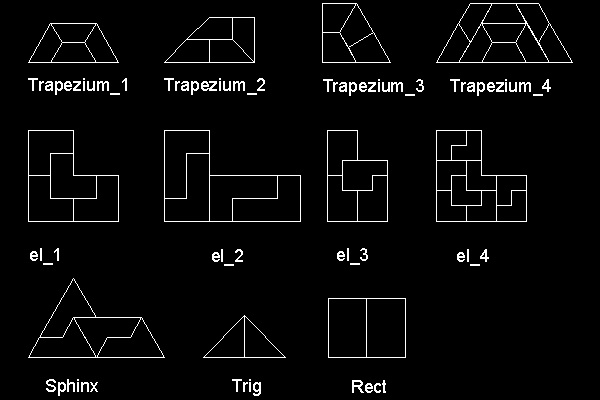
Name under each shape denotes the command to execute the program.

************************* sphinx_tile.dwg ************************

You can see the process in animation.

To create this drawing and animation:
Load reptiles.lsp (load "reptiles")
Then from command line, type sphinx

More examples

It is a fun to try various colors for each tile.The author used the following color pattern for the example shown below. Background color also makes a big difference. Try you own ideas and have fun.

Color Pattern

************* shade_trape_1.dwg ************ ************** shade_trape_2.dwg ************

************* shade_trape_3.dwg ************ ************** shade_trape_4.dwg ************

************* shade_el_1.dwg ************ ************** shade_el_2.dwg ************

************* shade_el_3.dwg ************ ************** shade_el_4.dwg ************

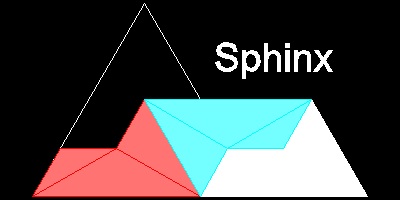
************* shade_sphinx.dwg ************

Output examples

************* trapezium_1_shade.dwg ************ ************** trapezium_2_shade.dwg ************

************* trapezium_3_shade.dwg ************ ************** trapezium_4_shade.dwg ************

************* el_1_shade.dwg ************ ************** el_2_shade.dwg ***********

************* el_3_shade.dwg ************ ************** el_4_shade.dwg ***********

************* trig_shade.dwg ************

7. Dedeney's Circle Quizzes (Ref 1)

According to G.N.Frederickson, the following puzzle (7.1) was originally proposed by John Jackson(1821). He was a "Private Teacher of the Mathematics", who lived in England from 1793 to 1875.

7.1 Table-top and stools (ref 1 pp.38-39)

This is the quote from ref 1.
"The story is told that an economical and ingeniuous schoolmaster once wished to convert a circular table-top,for which he had no use,into seats for two oval stools,each with a hand-hole in the centre. He instructed the carpenter to make the cuts as in the illustration and then join the eight pieces together in the manner shown. So impressed was he with the ingenuity of his performance that he set the puzzle to his geometry class as a little study in dissection. But the remainder of the story has never been published ,because , so it is said,it was a characteristic of the principals of academies that they would never admit that they could err. I get my information from a descendant of the original boy who had most reason to be interested in the matter."

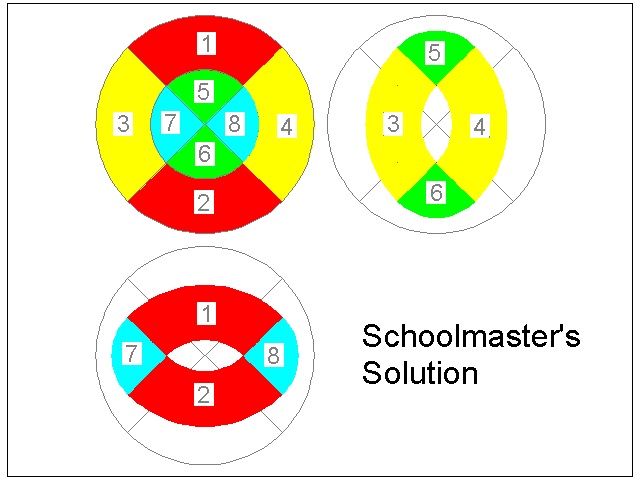
************************ Download this drawing(DWG format) **********************

"The clever youth suggested modestly to the master that the hand-holes were too big, and that a small boy might perhaps fall through them. He therefore proposed another way of making the cuts that would get over this objection. For his impertinence he received such severe chastisement that he became convinced that the larger the hand-hole in the stools the more comfortable might they be.
Now what was the method the proposed ? Can you show how the circular table-top may be cut into eight pieces that will fit together and form two oval seats for stools (each of exactly the same size and shape ) and each having similar hand-holes of smaller dimensions than in the case shown above ? Of course, all the wood must be used"

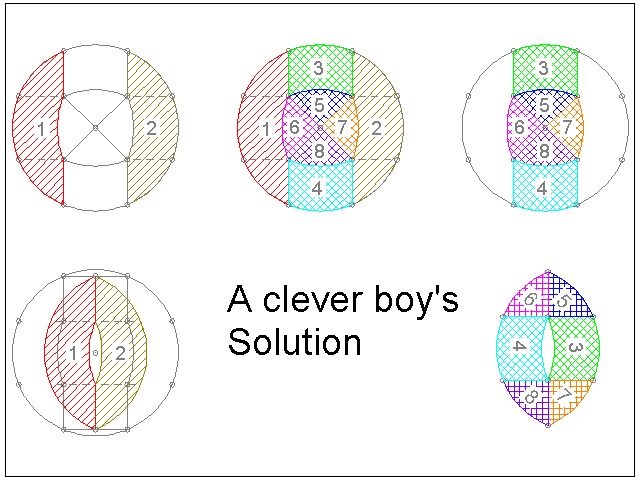
************************ Download this drawing(DWG format) **********************

Four piece solution

If the number of cut pieces is reduced to four, there is a very interesting answer.
Dudeney atributed the following beautiful 4-piece dissection to Sam Loyd (Ref 14, 15).

************************ Download this drawing(DWG format) **********************

Sam Loyd's another solution for Oval stool quiz

Sam Loyd also came up with one more solution for oval seat tops quiz.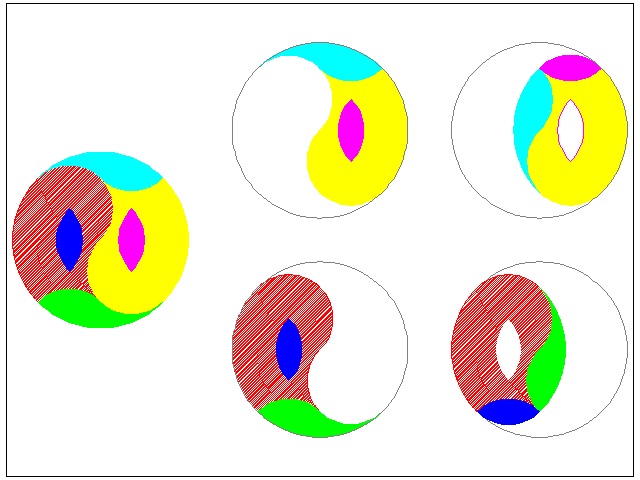

************************ Download this drawing(DWG format) **********************

Frederickson's another solution for Oval stool quiz

G.N.Frederickson also came up with one more solution for oval seat tops quiz.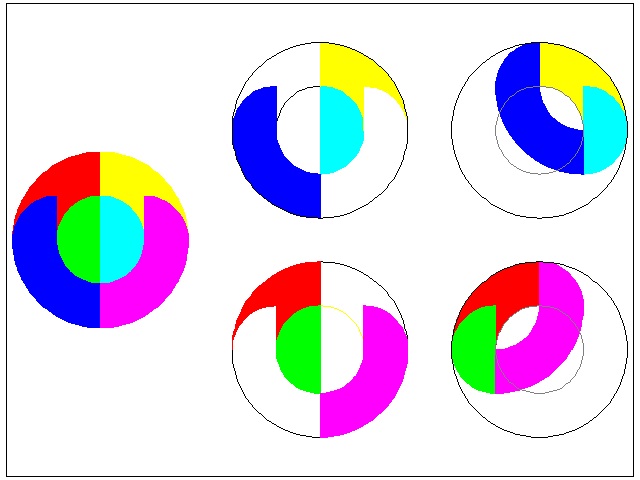

************************ Download this drawing(DWG format) **********************

Comparison of stool size and hand-hole size

Since a clever boy's solution claims that its hand-hole size is smaller, it is intersting to see the difference among the hole and overall sizes of the above 3 plans. For comparison purpose, the original circular table size is set to 2 units(2.0) in radius.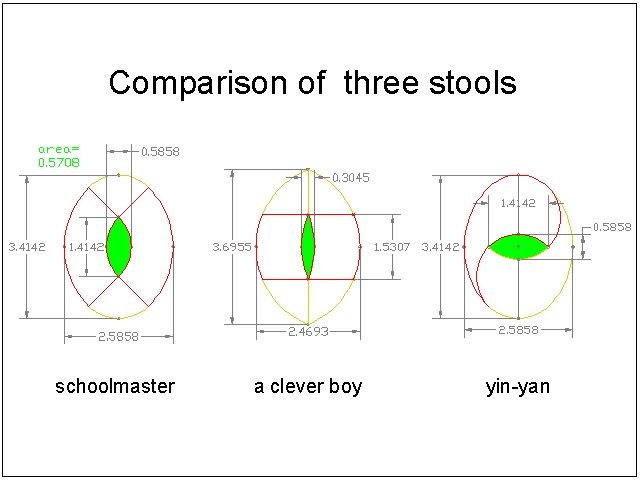

************************ Download this drawing(DWG format) **********************

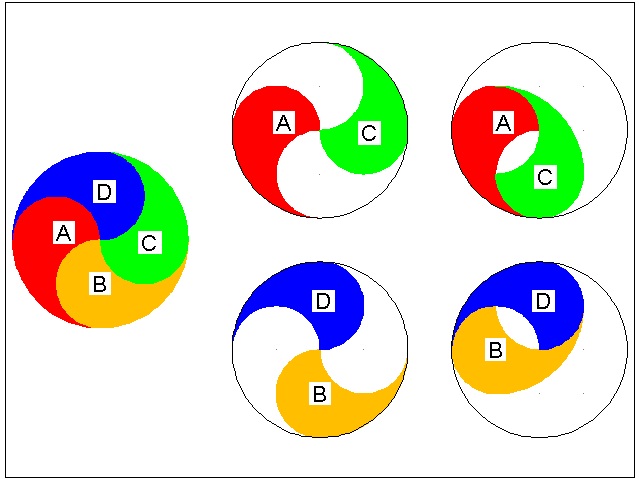
7.2 The Great Monad (or Ying-Yang) quiz #1

Here is the quiz #1 in its original form.
(I) Which has the greater area, the inner circle containing the Ying and Yang,or the outer ring ?

(II) Divide the Ying and Yang into four pieces of the same size and shape by one cut.

(III) Divide the Ying and Yang into four pieces of the same size, but different shape, by one cut.
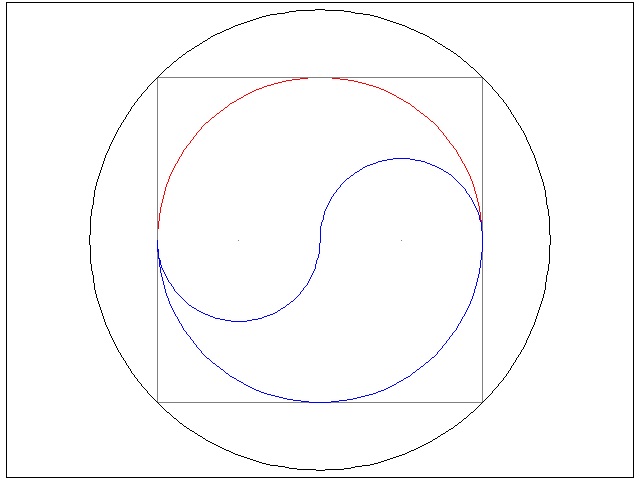
*************************** Download this drawing(DWG format) ************************
Solutions
The areas of circles are to each other as the squares of their diameters.
The diameter of the outer circle is square root of 2 times of that of the inner one. So the arearatio is 2 to 1. Therefore the areas of the outer ring and the inner circle is equal.
This answers the question #1.
The illustration below answers the question #2 nd 3.
Four pieces of Ying-yang is the answer for #2.
The diagonal line X-Y is the answer for question #3.
The reason: The areas of D & E are equal, and line X-Y divides them in half.
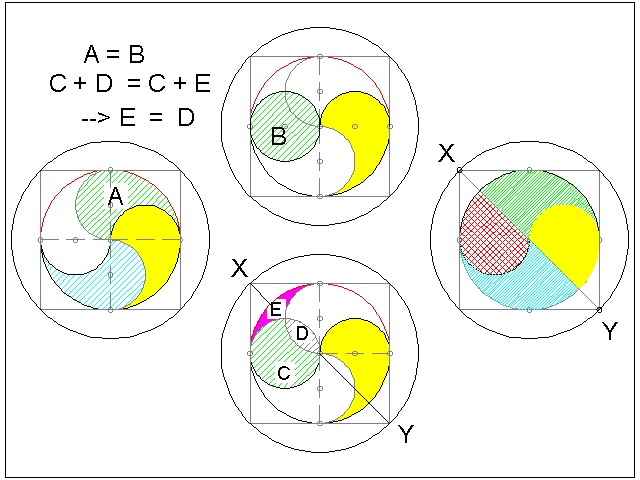
************************ Download this drawing(DWG format) **********************

7.3 The Great Monad (or Ying-Yang) quiz #2

In 19-th century England, horseshoes were considered "lucky". It is a very old superstition, and
most houses at the West End of London had a horseshoe on the threshhold. Even Lord Nelson
had one nailed to the mast of the flagship Victory.
The puzzle was to cut the two shoes into four pieces, two pieces each, that would fit together and form
a perfect circle. It was also stipulated that all four pieces should be different in shape.

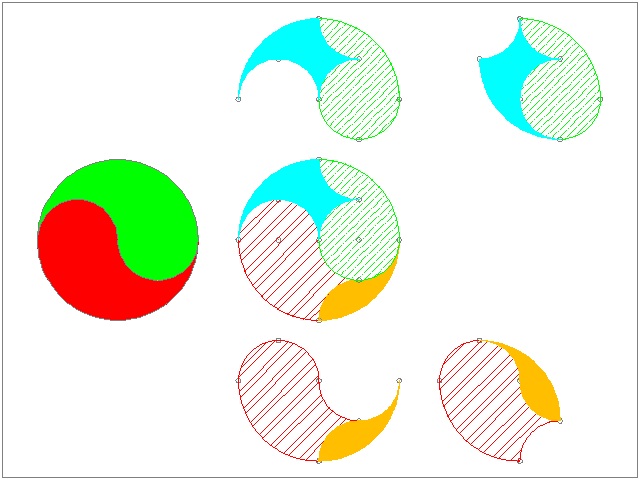
************************ Download this drawing(DWG format) **********************

7.4 Japanese emblems resembling Ying-yang symbol

Japanese emblems looking similar to Ying-yang are called "Tomoe", but their origins are totally different. There are many variations, and the first three are the typical. The last image is my creation. A few reference for English readers are listed.

To download, click the hypertext at the top of each image.

Download this image Download DWG file Tomoe picture #1	Download this image Download DWG file Tomoe picture #2
Download this image Download DWG file Tomoe picture #3	Download this image Download DWG file Tomoe picture #4

8. Sam Loyd's Red Spade Quiz (Ref 14)

According to ref.14, Sam Loyd saw a stained glass decoration depicting a "red spade", although the insignia of the club house was supposed to be "the ace of hearts". Upon further inspection he found out that this "red spade" was composed of three pieces. He then figured out that by proper arrangement of the three pieces, they would be fitted together so as to form the "ace of hearts", as originally desired. He then proposed the following quiz.
"Show how to change a spade into a heart"
The first thing the author to find out is what is really the shape of "heart" and "spade". http://en.wikipedia.org/wiki/Heart_(symbol) lists 3 heart shapes which can be expressed in analytical form : Classical "cardioid", implicit form in Cartesian coordinate(x,y), and parametric form in polar coordinate.
It has been less successful regarding the shape of "spade".
So I have decided to reverse the direction of the propostion, and tried to dissect an heart shaped figure into "spade" look-like figure. Three results are shown below. I also colored Heart and Spade according to the commonly accepted way.
See how the color changes from red to black counter clockwise as "Heart" is transformed into "Spade"..

8.1 Solution by common analytical "heart" curves

Cardioid
R = a*(cost + 1)

************************ Download this drawing(DWG format) **********************

Parametric form in polar coordinate
x = 16 sin³t
y = 13 cost - 5 cos2t - 2cos3t - cos4t

************************ Download this drawing(DWG format) **********************

Implicit form in Cartesian coordinate
f(x,y) = (x² + y² - 1)³ - x²y³ = 0
Note from the author: Using the polar coordinate, this curve can be rewritten as
f(r,t) = (r² - 1)³ - r⁵(cost)²(sint)³ = 0
Then for a given angle t, search the root for r using Newton iteration.

************************ Download this drawing(DWG format) **********************

It is clear that none of the above give a beautiful set of heart and spade.
The biggest problem is that the resulting spade has a sharp spiked tip.
To avoid this , the starting heart shape must has a rather flat bottom like cardioid. But cardioid does not have a sharp mound on the top, so it is hard to be called a heart shape.
This motivate the author to explore other methods of drawing "heart shape".

8.2 Other methods of making heart shape

Dissecting ellipse
It is well known that cutting an ellipse through the center line, and add a mirror image will create a heart shape (See above section 1.6 Ellipse to heart)

************************ Download this drawing(DWG format) **********************

Archimedes' Spiral to heart
Archimedes spiral is defined as R = k * t
where R is a distance from the coordinate origin, k is constant, and t is angle in radian.

************************ Download this drawing(DWG format) **********************

Fermat's Spiral to heart
Fermat's Spiral is defined as R = sqrt(t) * K
where R is a distance from the coorinate origin, K is a constant, and t is an angle in radian.

************************ Download this drawing(DWG format) **********************
The author thinks that Fermat's heart may qualify to be a candidate for "Hear to Spade" dissection.

8.3 Further studies on heart shapes

References

Dudeney,Henry E.: Amusement in Mathematics. Dover, 1958. The original was published in 1917.
Cundy,H.M.,Rollett,A.P.: Mathematical Models. Oxford Univ. Press, 1961. First edition published in 1951 .
Lindgren,Harry: Recreational problems in Geometric Dissections & How to solve them. Dover, 1972.
Frederickson,Greg N.: Dissections: Plane & Fancy. Cambridge Univ. Press, 1997.
Frederickson,Greg N.: Hinged Dissections: Swinging & Twisting. Cambridge Univ. Press, 2002.
Wells, David: The Penguin Dictionary of Curious and Interesting GEOMETRY. London,England: Penguin Books, 1991.(Out of print)
Nelson,R.B. : Proofs Without Words II: More Exercises in Visual Thinking. MAA, 2000.
Langford,C.Dudley: "Use of a geometric puzzle", Mathematical Gazette,No.260,1940.
Abe, Hisashi: "Amazing Origami"(in Japanese),2003. ISBN 4-535-78409-4
Anderson,M.,Katz,.V.,Wilson,R,:Sherlock Holmes in Babylon,MAA,2004
Haunspenger,D., Kennedy,S. editors: "The Edge of the Universe",MAA, 2006
Millington,Jon : "Curve Stitching",Tarquin Publications,2001
Alexanderson,G.L.,Seydel,K. : "Kürschák's tile",Mathematical Gazette,No.421,1978.
Loyd, Samuel : Sam Loyd's Cyclopedia of 5000 Puzzles,Tricks & Conundrums with answers, first printing in New York in 1914, The Lamb publishing Co., Second Printing in 2007 by Ishi Press International. ISBN 978-0-923891-78-7
Gardner, Martin.: Mathematical puzzles of SAM LOYD. Dover, 1959. The original was privately published in 1914 by Sam Loyd.
Dower,John : "The Elements of Japanese Design", Weatherhill,1971
trnslated by Adachi,Fumie : "Japanese Design Motifs", Dover, 1972
http://www.otomiya.com/kamon/lika/tomoe.htm