Distance to the Sun
Aristarchus's experiment to measure the Distance to the Sun
According to (Ref.3) A Manual of Greek Mathematics,"Intermediate between Euclid (325BC - 265BC) and Archimedes (287BC - 212BC) comes Aristarchus of Samos(310BC - 230BC), famous as the Copernicus (1473 - 1543) of antiquity. Perhaps about 25 years earlier in date than Archimedes, he made an observation of the summer solstice in 281 B.C. .... But the Greeks knew him as "Aristarchus the Mathematician", a title which he justified by his brilliant application of mathematics to astronomy in one work of his which is extant, "On the sizes and distance of the Sun and Moon". We gather that his principal interest was in astronomy. Aristarchus's crowning achievement was the hypothesis he put forward regarding the solar system,wherein he anticipated Copernicus. ...his hypothesis being "that the earth revolves about the sun in the circumference of a circle,the sun lying in the middle of the orbit,.... the size of the earth's orbit about the sun is negligible in comparison with the size of the whole universe."
Basic assumptions
Aristarchus made several assumtions, and two of them are (Ref. 3)(1) When the moon appears to us halved, the great circle which divides the dark and the bright portions of the moon is in the direction of our eye(the effect of which is that at the time of dichotomy the centres of the sun,moon, and the earth, say,S,M,E,form a triangle right-angled at the center of the moon.)
(2) When the moon appears to us halved,its distance from the sun is then less than a quadrant by one-thirtieth of a quadrant(that is,the angle SEM in the right-angled triangle is 87 degrees).
So the figure below shows the model he used to measure the distance to the sun as a multiple of the distance between the earth and moon. The angle "X" which can be measured during the sunset in the First quarter moon phase (The quarter moon in the zenith, and the sun is about to set below the horizon.) Aristarchus assumes the angle SEM to be 87 degrees ,where as it is in fact 89 degrees and 50 minutes. With the measuring devices available in his time, this value must have been the most accurate.
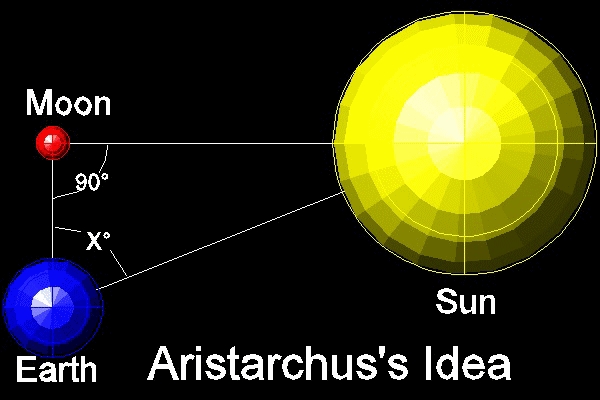
************************ Aristarchus_00.dwg ************************
The model with actual dimensions
The sizes of the Sun,The Moon and the Earth and their distances to the Earth are shown in the following table.
| Radius-km(mile) | Ratio to Earth's Radius | Distance to the Earth-km(mile) | Ratio to the Moon-Earth distance | |
|---|---|---|---|---|
| Sun | 695,000 (431,945) | 109 | 147e6~152e6 (91.341e6~94.448e6) | ~41 |
| Earth | 6,378 (3,964) | 1.0 | ||
| Moon | 1,737.4 (1,079.8) | 0.273 | 356,749~406,282 (221,000~253,000) | 1.0 |
The model was set up such that Moon and Sun lies on X-axis and the Earth is down Y-axis by the length of Moon-Earth distance. The actual model looks like this.
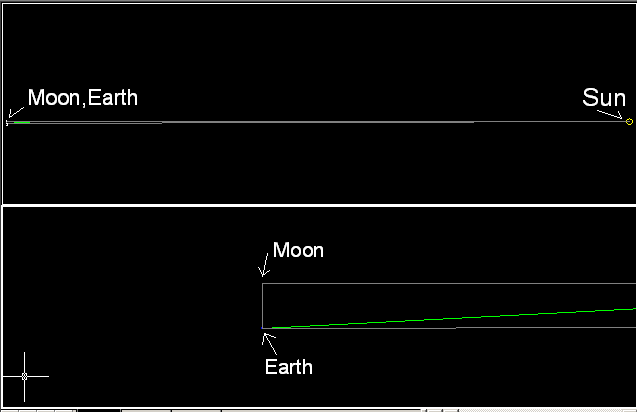
************************** Aristarchus_03.dwg **************************
The next picture shows how a line is drawn from the center of the earth with 87 degrees from Moon-Earth line. The intersection of this green line with Moon-Sun line is the position of the Sun according to Aristarchus' assumption.
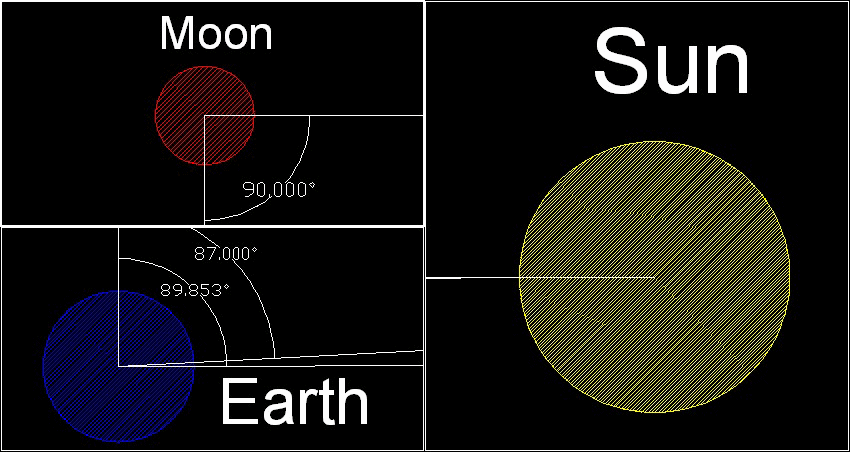
*************************************** Aristarchus_01.dwg ***************************************
The result
Aristarchus' conclusion:
"The distance of the sun from the earth is greater than eighteen and less than twenty times the distance of the moon from the Earth."
Letting the average distance between Moon and the Earth be about 384,400 km (239,000 mile), Aristarchus's result states that the distance is farther than 384,400 x 18 = 6,920,000 km , but shorter than 384,400 x 20 = 7,690,000 km. The actual result based on the angle X = 87 degress is 7,335,000 km,which is correctly within his estimated range. The essence of the matter is that,in order to prove his theorems,Aristarchus requires values for certain ratios which are the equivalent of the trigonometrical sines and cosines of certain small angle, and in particular those of the angles 3 degrees and 1 degree.He shows that they lie between certain limits. The reader have to be reminded that the trigonometry was born more than 1500 years after Aristarchus.
*************************************** Aristarchus_02.dwg ***************************************
To create this drawing :
Load Aristarchus_model.lsp (load "Aristarchus_model")
Then from command line, type (setup_aristarchus)
Then split windows into 2 horizontal viewports, and zoom-in to Moon-Earth area.
References
- Atlas of the SKIES, Surrey,England: TAJ Books,2003
- Heath, Sir L.H.: A History of Greek Mathematics,Vol II. Dover Edition, 1981. Originally published in 1921
- Heath, Sir L.H.: A manual of Greek Mathematics. Dover Edition ,1963. Originally published in 1931.
Go to Fun_Math Content Table Earth Moon & Sun
All comments should be sent to Takaya Iwamoto
Last Updated July 9-th, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.