Estimating the size of the Earth
Eratosthenes(276BC - 194BC)' Book "On Measurement of the Earth"
According to (Ref.3) A Manual of Greek Mathematics,"Eratosthenes of Cyrene was a man of great distinction in all branches of knowledge...Thus he was called an all around athlete. ... Eratosthenes' most famous achievement was his measurement of the earth."
Basic assumptions
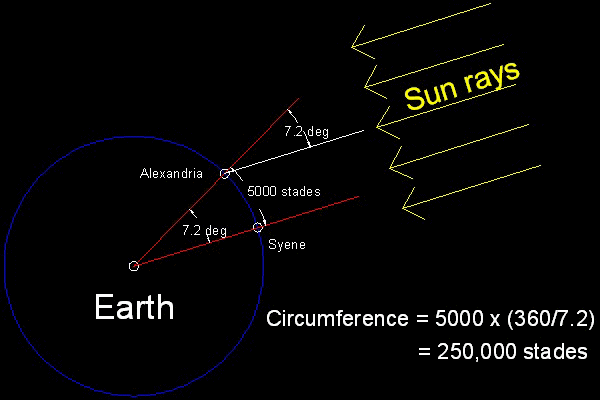
In his book he made the following assumptions.- The earth is a shere.
- The sun was so far away that its rays were essentially parallel.
- Syene and Alexandria is on the same meridian
- The distance between Syene and Alexandria is known---5,000 stades
- On the day of summer solistice, the sun is exactly above Syene.
- At the same moment in Alexandria, the inclination of the sun's ray to the vertical is 1/50th of a complete circle (= 7.2 degrees)
**************** Eratosthenes_base_model.dwg ****************
The discussion on the accuracy of the result
There is no flaw in the approach Eratosthenes took, and the accuracy depends totally on how to convert the unit of length "stades" to our modern units(km or mile). If we convert his result (250,000 stades) using 40 stades = 6.3km (3.915 mile),then we obtain for the circumference of the earth along meridian = (250,000 / 40) x 3.915 = 24,665 miles, and for the diameter 7789 miles ,which is only 85 miles shorter than the true polar diameter. The error is only 1 per cent !!. But his result was later modified as 252,000 stades probably because this number can be divided by 60 and easy to use for calculation.(Calculation in those days was based on 60's.) 252,000 stades will be translated into the polar diameter value of 7850 miles,which is a much better estimate (only 24 miles shorter(only 0.3 % off !!!). (Ref) Radius of the Earth (Min 6336 km(3937 mile) Max 6399 km(3976 mile)) The earth is not a perfect sphere but an oblate ellipsoid (slightly egg-shaped),the circumferential distance of which are shorter in polar direction than the equatorial direction.Ref: Bob Chamberlain : "What are some algorithms for calculating the distance between 2 points ?"The model simulation with ACAD
According to Latitude and Longitude ,the latitude and longitude values for two places in Egypt are| Latitude | Longitude | |
|---|---|---|
| Alexandria,Egypt | 31.2 N | 29.9 E |
| Syene(Aswan),Egypt | 24.088 N | 32.899 E |
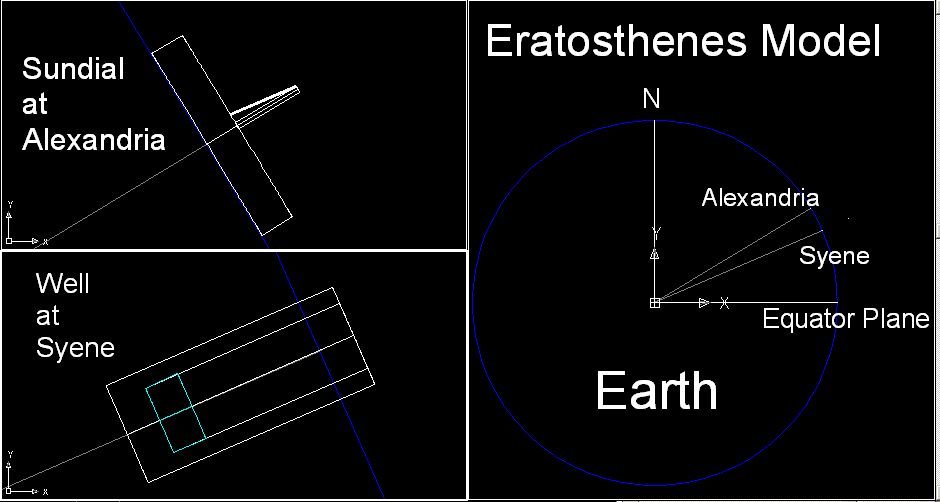
The longitude value for Syene differs slightly from that of Alexandria (difference is almost 3 degrees), and since one degree is about 69 miles apart, Syene must be about 200 miles west of the present day Aswan. Here in our model, longitude value of Syene is assumed to be 29.4 E, so that Alexandria and Syene are on the same meridian. At Alexandria a sundial is erected to measure the inclination angle on the summer solstice. The pole is 3 meters high and its radius is 10 cm(0.1 m). At Syene, a Well is drilled to show that when the Sun is on The Tropic of Cancer, the Sun does not cast any shadow on the bottom of the well. The dimension of the well is 5 meters deep from the ground, and its inner radius is 1 meter. Also added here is a body of water at the bottom of the well.This is how the model looks.
*************************************** Eratosthenes_model_2.dwg ***************************************
To create this drawing :
Load Eratosthenes_model2.lsp (load "Eratosthenes_model2")
Then from command line, type measure_earth
Author's Note:
When the original model was created,the height of the sundial's pole length was set to 3 meters,with its diameter 0.2 meter.
But the shadow making rendering process did not work well for this scale difference(compared to the Earth's diameter). So the scale of pole and well are
bumped up 3 orders of magnitude. If the earth is erased before the rendering process, maybe the original scale would be OK,
but author have not verified it yet. Just for the viewing purpose , the author should have treated both sundial and well independently
of the earth.
Eratosthenes Model illustration done by CAD
Following four different light directions are selected. The angles are inclination to the equatorial plane:
| Season | Angle | cosine | sine |
|---|---|---|---|
| Summer Solstice | 23.5 | 0.91706 | 0.39875 |
| Angle 12 deg | 12.0 | 0.97815 | 0.20791 |
| Vernal and Autumnal Equinox | 0.00 | 1.00000 | 0.00000 |
| Winter Solstice | -23.5 | 0.91706 | -0.39875 |
Note:
Distant light definition in AutoCAD will take only 2 decimal places. So ,for example, cosine values for 0.917 and 0.924 are input as 0.92.Sundial at Alexandria
The pole of the sundial cast shadows, and at the time of Summer Solstice, the line connecting tip of the shadow and the pole top and the pole is 7.2 degrees,which is the difference of the latitude angle. That imaginary line is also added to the rendered picture for reference purpose.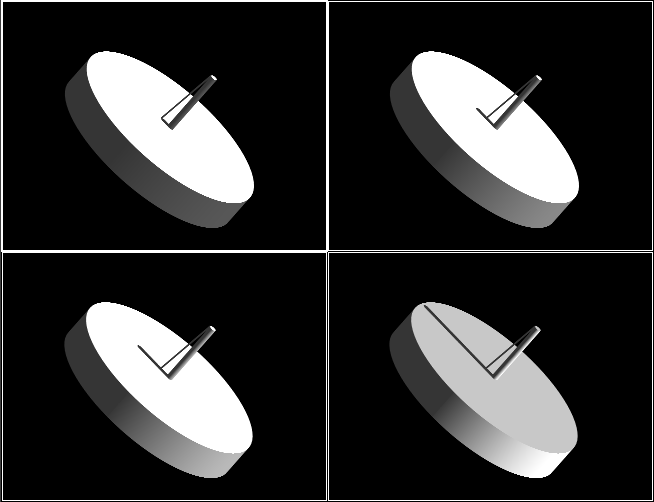

**** earthsize_win_id.dwg ****
********************** sundial_at_Alexandria.dwg **********************
Animation is now being prepared.
To create this drawing :
Load Eratosthenes_model2.lsp (load "Eratosthenes_model2")
Then from command line, type measure_earth
At this stage, AutoCAD displays Eratosthenes_model_2.dwg.
In order to get rendering image, additional steps are required.
The following steps are specific to AutoCAD.
(1) Select the upper left viewport, and using VPORTS command, make a single viewport.
Erase the blue line representing the earth.
(2) Using 3DORBITS command , rotate the sundial as shown in the drawing above.
(3) Using VPORTS command , split into 4 viewports.
(4) For each viewport, specify the direction of the distant sunlight.
Here it is importan to select SHADOWS ON and Volumetric/Raytraced shadows option.
(5) Use RENDER command to render the drawing.
Well at Syene
View is looking down the well from the center line of the well. Cyan color is the water at the bottom of the well. At the time of Summer Solstice, there is no shadow on the water in the well.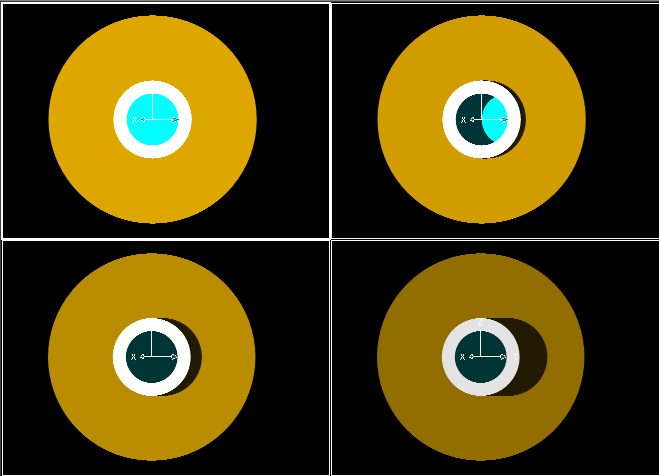

**** earthsize_win_id.dwg ****
**************************** well_at_Syene.dwg ****************************
Animation is now being prepared.
To create this drawing :
Load Eratosthenes_model2.lsp (load "Eratosthenes_model2")
Then from command line, type measure_earth
At this stage, AutoCAD displays Eratosthenes_model_2.dwg.
In order to get rendering image, additional steps are required.
The following steps are specific to AutoCAD.
(1) Select the lower left viewport, and using VPORTS command, make a single viewport.
Erase the blue line representing the earth.
(2) Using VPOINT command , input !pnt_syen to specify the viewing direction.
(3) Using VPORTS command , split into 4 viewports.
(4) For each viewport, specify the direction of the distant sunlight.
Here it is importan to select SHADOWS ON and Volumetric/Raytraced shadows option.
(5) Use RENDER command to render the drawing.
References
- Atlas of the SKIES, Surrey,England: TAJ Books,2003
- Heath, Sir L.H.: A History of Greek Mathematics,Vol II. Dover Edition, 1981. Originally published in 1921
- Heath, Sir L.H.: A manual of Greek Mathematics. Dover Edition ,1963. Originally published in 1931.
Go to Fun_Math Content Table Earth Moon & Sun
All comments should be sent to Takaya Iwamoto
Last Updated July 9-th, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.