All Curves are made up of many circles - Evolute
The main lesson of this section is that any curve is made up of a number of true circles.
(Note: a straight line segment is interpreted as a circle with an infinitely large radius.)
Take a look at the simple drawing below:
***********************************curve_sample_1.dwg ***********************************
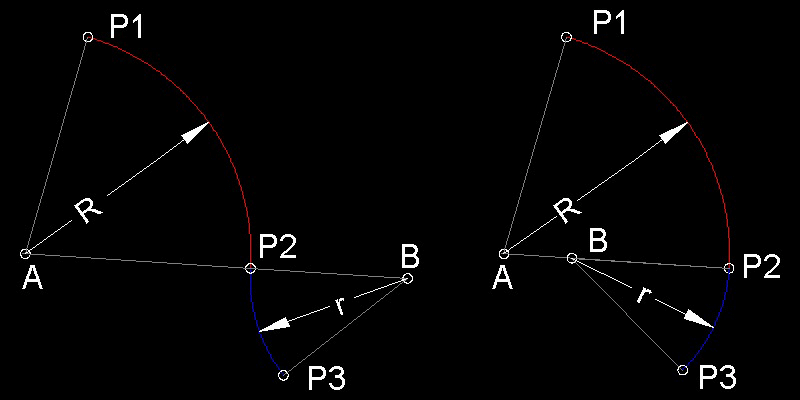
Both curves are made up of Arc A-P1-P2 with radius R and Arc B-P2-P3 with radius r.
The difference is the locations of the second Arc's center (point B).
It is also important to observe that the point where the radius changes (point P2) and
the center of 2 arcs(point A & B) are co-linear
This will guarantee the continuity of the slope ( or tangent ) at point P2.
In order to draw a smooth continuous curve made up of multiple arcs, the following rule must
be applied:
"At the point where radius changes, the center of the new radius must be on the line
connecting the point and the previous arc center."
In this example, when the first arc comes to the end point P2 where the radius is reduced
from R to r, the center of the arc moves along the line connecting the previous arc center
"A" and point P2 to point "B", then new arc starts from there. By so doing, the slope at point P2
,which is actually a tangent common to both Arcs, is continuous and guarantees a smooth looking curve.
Here is another simple drawing to prove the point.
***************************************ying_yang.dwg ***************************************
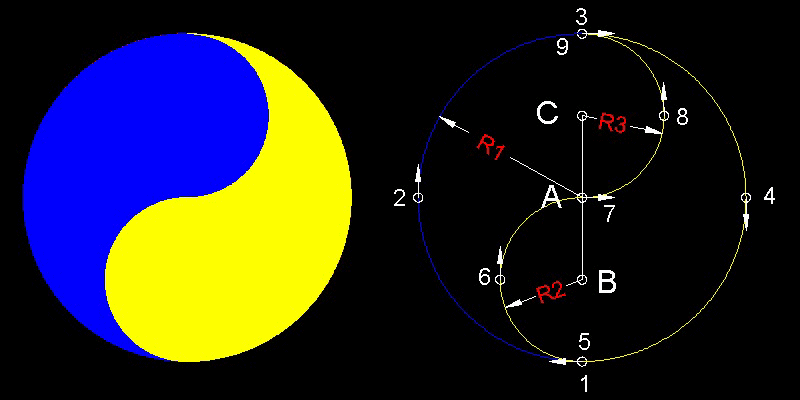
The numbers in the drawing denote the sequence of the arc's move. The first change of the centers of arcs
happens
when the arc reaches point "5". The change is along the line connecting "A" to "5".
Similarly, at point "7", the move of the center
is on the extension line connecting "B" and "7".
You can see the process in animation .
To create this drawing and animation:
Load ying_yang.lsp (load "ying_yang")
Then from command line, type ying_yang
In the 2 examples shown above, the center of the curvature (= circle) moves along a line segment, but,in general,
if the
curves are more complex (like the shape of Egg, for example) , the centers of the circles moves along a curve.
This curve is called "Evolute".
Definition: The evolute of a curve is the locus of its centers of curvature.
How to use Evolute to draw an ellipse approximately
Our goal here is to draw a real chicken egg shape using several arcs. The analytical curve which resembles
closest to Chicken's egg shape is an ellipse.
The difference is that , in general, chicken-egg-shape has two end radii
with its top end having a radius smaller than the bottom end.
If we are successful in finding a general method
for drawing a real-chicken-egg-shape , the same method has to be applicable to an ellipse,which is a much
simpler shape.
So let us first try to draw an ellipse using the concept of Evolute.
Step 1: define evolute for an ellipse
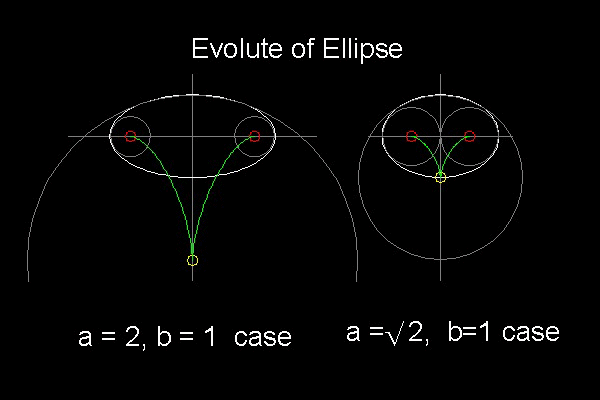
For an ellipse defined by (x/a)2 + (y/b)2 = 1 , ( assuming a > b )the evolute is given by (x/A)2/3 + (y/B)2/3 = 1 where Aa = Bb = a2 - b2
and the smallest radius(r) and the largest radius(R) are r = b2/a , R = a2/b
Two evolute curves for 2 different ellipses are shown below. Since th ellipse is symmetric wrt x-axis,evolute for the upper half is considered.
To create this drawing:
Load evolute.lsp (load "evolute")
Then from command line, type draw_ellipse_evolute
After making one evolute, move this to the left, and make another .
When we observe these drawings, we see that an ellipse can be drawn approximately by a small and large arcs
and one more arc bridging them.
The question is how to find the "bridging" arc.
The concept of "Radical Axis" can be used to define the
"bridging" arc.
**********************ellipse_evolute_2.dwg **********************
Step 2: Radical Axis: (a) How to get it
The following argument applies to any two circles in general, but since we are dealing with an ellipse, circle C1(= C ) is a circle with radius b2/a ,and C2(= C' ) is a circle with radius a2/b.
Analytically:
Circle C : C (x,y) = x2+y2+ 2gx+ 2fy+c =0
Circle C': C'(x,y) = x2+y2+2g'x+2f'y+c'=0
Then C(x,y) - C'(x,y) = 0
is called the "Radical Axis" of the Circle C and C',
and its line equation is written as follows:
2(g - g')x + 2(f - f')y + c - c' = 0
or this can be written as x/ Xo + y/Yo = 1
The coordinate of the points this line intersects X & Y axis are
Xo = -(1/2)(c-c')/(g-g') , Yo = -(1/2)(c-c')/(f-f')
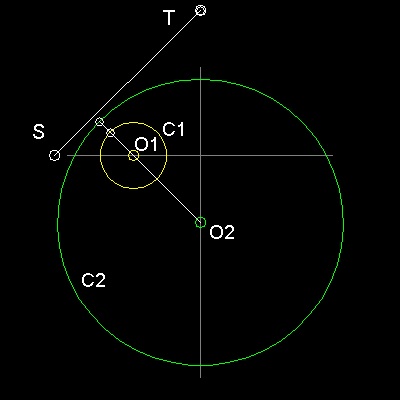
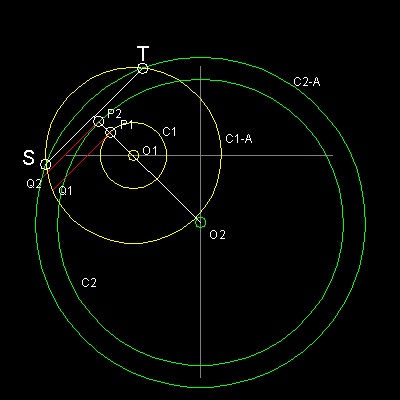
They are shown as points S and T in the drawing. The line segment ST is the locus of points from which
the tangents to both circles have the same length !!
************radical_axis_1.dwg ************
To find out the points S,T given two circles:
Load evolute.lsp (load "evolute")
Then from command line, type radical_axis and select two circles.
This will draw line ST in the drawing.
Graphically:
The line connecting the centers of two circles intersect two circles at points P1, and P2
2 line segments P1Q1, and P2Q2 (P1Q1 = P2Q2) are erected at these points
normal to the line O1O2.
Draw a circle C1-A with its center at O1 and radius O1Q1.
Similarly, draw a circle
C2-A,with its center O2 and radius O2Q2.
Intersecting points of these 2 circles are point S and T.
Line ST is the Radical Axis of circles C1 & C2.
************radical_axis_2.dwg ************
Step 3: Radial Axis: (b) How to use it
Important properties of "Radical Axis":1. Line ST is normal to line O1O2.
2. The length of tangent lines drawn from a point on line ST are the same for Circles C1 and C2.
This last property can be used to find an evolute and its associated circle to fill the gap between circles C1 and C2.
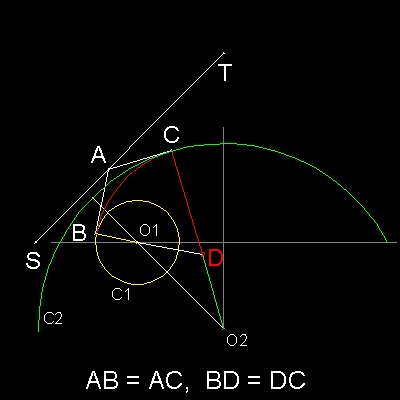In the drawing (left), A is a point on the line segment ST.
B, C are the end points of tangent lines from A to circle C1 & C2.
Connect point C and O2.
The intersection of line CO2 and the extension of line BO1 is point D.
Since ST is a radical axis, AB = AC,
and both angles ABD & ACD are 90 degrees, BD = CD.
Therefore if point D is selected as
an evolute between O1 and O2,
we have a smooth continuous curve made up of 3 arcs.
First arc :center at O1, and starts from x-axis to point B.
Second arc:center at D, starts from B and ends at C.
Third arc :center at O2,starts at C to the point symmetric to point C wrt Y-axis.
************radical_axis_3.dwg ************
Steps to draw an ellipse using 5 circles
E.H.Lockwood demonstrated that an ellipse can be drawn by compass and straight edge.Ref.3 & 4.
************************************ellipse_Lock_01.dwg ************************************
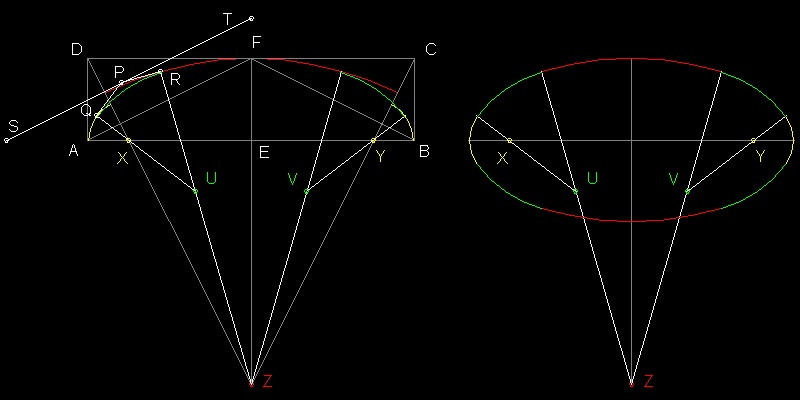
Steps to draw an ellipse using 5 circles
- Draw a rectangle, where AB = 2a, BC = AD = EF = b
- Draw a line from point D perpendicular to the line AF,which will intersect line AB at X, and line EF at Z.
Do the same to the right hand-side and call the intersection point "Y".
- Draw an arc centered at X with radius AX starting from "A" and ending at line XD. Do the same at point Y. This is an exact radius
at point "A" (= b2/a). Why ? --Triangles ADX and EAF are similar. So (AD/AX) = (AE/EF)
- Draw an arc centered at point "Z" with radius FZ starting from line DZ and ending at line CZ. This is an exact radius
at point "F" ( = a2/b). Why ? --Triangles DFZ and FEA are similar. So (DF/FZ) = (FE/EA)
- Draw a "Radical Axis" (line ST) using one of the methods described above. Select a point P on that line and
draw tangent lines to two circles,the end points of which are P & Q.
Extend QX and find intersection point U on the line RZ. Similar operation on the right hand side produces point V.
" 5 points, X,U,Z,V and Y is the evolute which yields an approximate curve ."