Many Shapes of Bird's Eggs: Classification of Egg Profiles
Regarding the classification of Egg profiles, the author has so far found only 2 references.Egg shape classification by Michael Walter(Ref. 2)
In ref. 2, Michael Walter used the following eight basic shapes.
1. Cylindrical : ex.hummingbird
2. Conical : ex northern lapwing, plover, kildeer
3. Pyriform : ex. common murre
4. Biconical : ex northern lapwing, plover, kildeer
5. Oval :
6. Elliptical : ex. bird of paradise, southern cassowary
7. Spherical : ex. common kingfisher
8. Longitudinal : ex.brown Kiwi
On page 12 of this beautiful book, there is a picture of 8 basic shapes Michael Walter uses
for classification of bird's egg shape. These samples are the real egg's image with
different size and shape. The smallest is the egg of hummingbird, the largest , that of Common murre . The author took a photo of this page and transferred to AutoCAD in jpg file format.After digitizing their contour lines, using the procedures described in the previous section, evolute curve(loci of the center of radii of the arcs forming the contour of the egg shape) are drawn for all of the eight egg shapes.Both contour and evolute curve define the characteristics of these egg shapes.
The result is shown below.
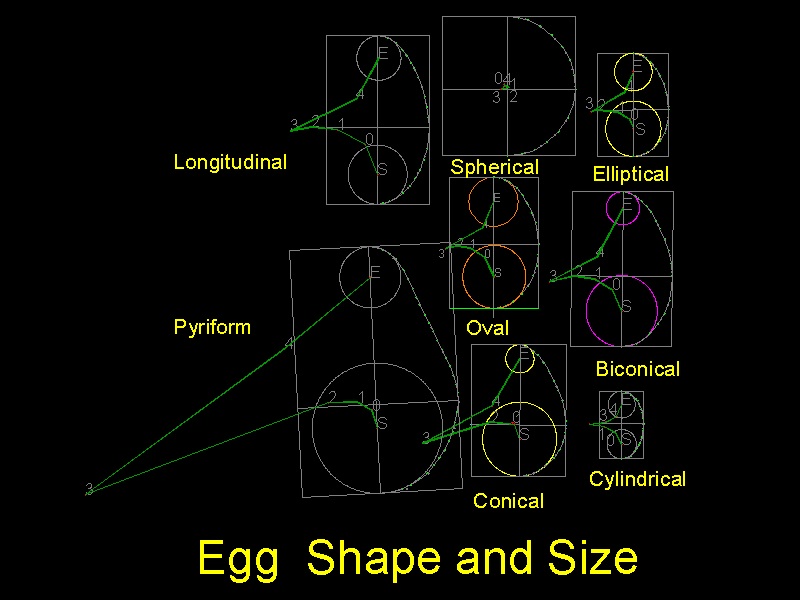
************************ Download this drawing(DWG format) **********************
Then
all of the egg's height are set to a unit value for comparison purpose(normalized).

************************ Download this drawing(DWG format) **********************
A "Oval" type egg shape is shown here as an example.
points in green color are created to define the contour , and those white points
are the equally divide points on this contour to find the center of curvature.
The similar processes are done for all shapes.
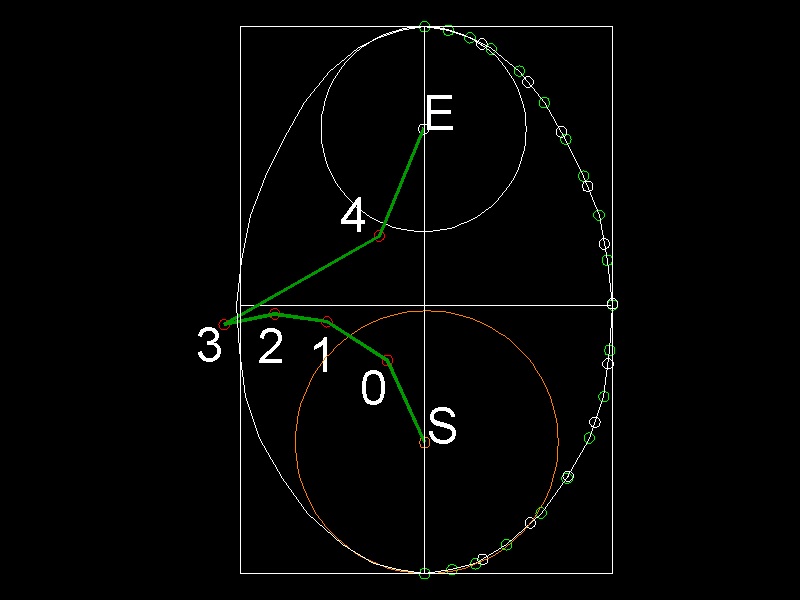
************************ Download this drawing(DWG format) **********************
Egg shape classification by Preston(Ref. 4,5)
In ref 4., four basic shapes ,proposed by Preston(Ref . 5), are discussed. The author has not read the content of Ref. 5 cited by ref. 4, so I just follow the description of ref. 4.
1. Spherical
2. Subelliptical
3. Oval
4. Pyriform
and each class is subdivided into 3 with superscripts, "Long", " "(Blank), and "Short",
(e.g. long-pyriform, subelliptical, short-oval, etc.).
The exception is elliptical,where "spherical" is used instead of "short-elliptical".
In total, there are 4 X 3 = 12 egg shapes.
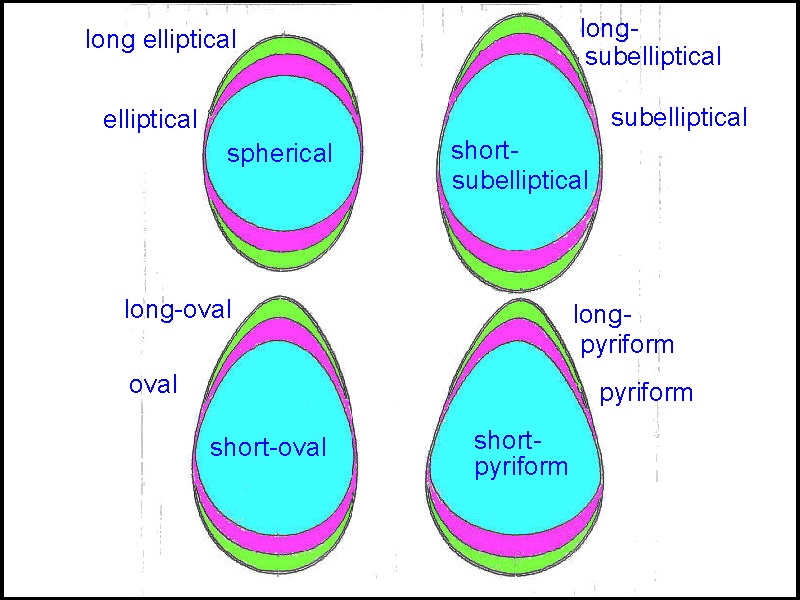
************************ Download this drawing(DWG format) **********************
Preston also define the following three statistical terms for the egg's shape.
Here L is the length of the egg, B is breadth, Rs the radius of
curvature of the blunt end, Rp, the radius of the small end.
Asymmetry -- a measure of the extent to which one end is bigger than the other,or
of "pyriformness". It is computed L(Rb - Rp)/B2
Bicone -- a measure of the extent to which the shape departs from the ellipsoid,apart from
departure caused by one end being bigger than the other. It is L(Rb + Rp)/B2 - 1
Elongation -- length divided by breadth: L/B
These three measures are calculated for the eight shapes used by Walter , and will be tabulated below: Since all the egg's curves are normalized(Their height is set to a unit value 1.0 ), one of the parameter, L , is set to 1.0 .
Data Tables (caluculated from "Egg Shape and Size" figure on the top)
| Shape | Breadth | Top Radius | Bot Radius | Asymmetry | Bicone | Elongation |
|---|---|---|---|---|---|---|
| B | Rp | Rb | ||||
| Cylindrical | 0.6442 | 0.1987 | 0.2167 | 0.043 | 0.001 | 1.552 |
| Conical | 0.7018 | 0.1076 | 0.2817 | 0.3530 | -0.210 | 1.425 |
| Pyriform | 0.6678 | 0.1239 | 0.2641 | 0.3140 | -0.1300 | 1.497 |
| Biconical | 0.6489 | 0.1072 | 0.2303 | 0.2920 | -0.1980 | 1.5410 |
| Oval | 0.6866 | 0.1874 | 0.2402 | 0.1120 | -0.0930 | 1.4560 |
| Elliptical | 0.6878 | 0.1826 | 0.2687 | 0.1820 | -0.0460 | 1.4540 |
| Spherical | 1.0 | 1.0 | 1.0 | 0 | 1.0 | 1.0 |
| Longitudinal | 0.6120 | 0.1319 | 0.1758 | 0.1170 | -0.1780 | 1.6340 |
Before going to the discussion about these classification, it may help the reader to clarify the
mathematical definition of the words like oval,pyriform, elliptical,etc . The author referred to Ref. 6 (The Words of Mathematics).
pyriform(or piriform) (adj.): from Latin pirum "pear". A piriform curve is pear-shaped.
Note: In Asian countries, "pears" look round like "apples",so ,in US, asian pears are called
"Apple pear".
oval (noun): from Latin ovum "an egg". An oval is egg-shaped. In mathematics an oval is a convex
closed curve that has an axis of symmetry. As the etymological connection to eggs implies, an oval is generally pointier at one end than at the other. In less strict usage,oval may be a synonym of ellipse.
spherical(adj.): from Greek sphaira "ball, sphere". A sphere is an ellipsoid that has all three axes equal.
cylindrical(adj.): from Greek kulindros "a roller".It is usually taken to mean a circular cylinder.
The following is the author's comments:
elliptical(adj.): having the shape of ellipse
longitudinal(adj.): longer lengthwise
conical(adj.): shaped like a cone
biconical(adj.): Both ends shaped like cones
Comparison of Michael Walter's 8 egg shapes
Now we are ready to compare these 8 "basic egg shape" among each other. Sphere is very unique and nothing to compare with. It is simply round like a ball.The author did the following comparisons.
1. Cylindrical vs. Elliptical
2. Conical vs. Biconical
3. Pyriform vs. Conical
4. Oval vs. Elliptical
5. Cylindrical vs. Elliptical
6. Biconical vs. Elliptical
7. Longitudinal vs. Biconical
The result is shown in the figure below.
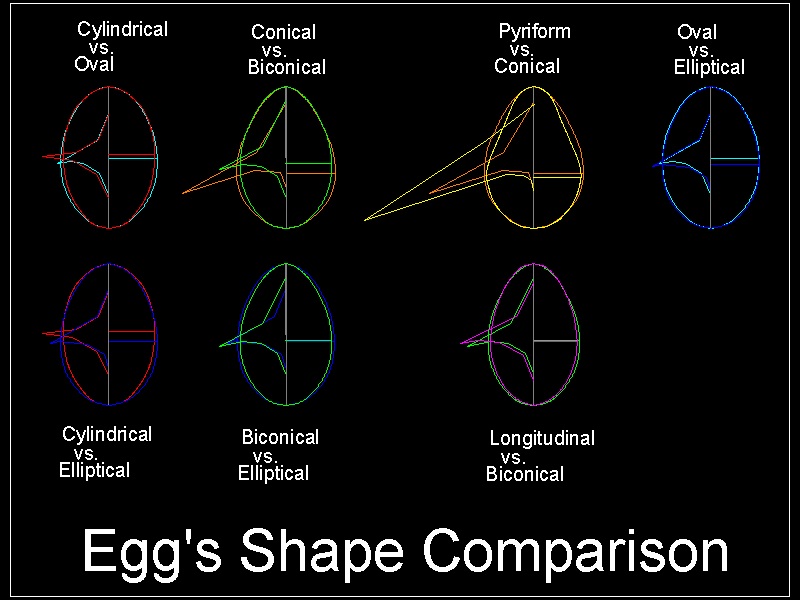
************************ Download this drawing(DWG format) **********************
Observation
Referring to the figure above :(1) Cylindrical vs. Oval : contours look almost identical on both ends, and the major
difference is the center of the max radii. This causes the difference of contour from the middle section toward the bottom. The line of the max width is in the middle for "cylindrical" as expected,
and that of "oval" is lower than that line.
(2) Conical vs. Biconical :difference of top and bottom radii is clearly observed.
(3) Pyriform vs. Conical :Upper portion of "pyriform" is almost a straight line, that is shown
as a way out position of the evolute point.
(4) Oval vs. Elliptical :Almost identical
(5) Cylindrical vs. Elliptical :discrepancy of "elliptical" from "cylindrical" is more pronounced
than case (1) above. Look at (4) Oval vs. Elliptical figure.
(6) Biconical vs. Elliptical :radii of both ends are bigger for "elliptical",which makes "elliptical" more bulky than biconical.
(7) Longitudinal vs. Biconical :Very similar except "longitudinal" is slightly flatter than "biconical".
Referring to the data table above :
Asymmetry :This is the index for the difference of top and bottom radii. Hence "conical", "pyriform" and "biconical" have values higher than the other. Note the values for symmetric shapes like "cylindrical" and "spherical" are zero as expected, and "oval" and "longitudinal" have almost same values, and "elliptical", a bit higher value.
Bicone : This is the index for the "protrudedness" at both ends.
"conical" has the highest value followed by "biconical","longitudinal" , "pyriform"
and "oval". It is a bit surprise that "pyriform"'s value is not that high.
Elongation : As expected "longitudinal" has the highest value, but
all other shapes' values are not far behind. The egg for Kiwi has a much higher value around 2.0 .
The author's personal opinion
(1) The basic shapes "oval", "elliptical" and "biconical" as represented in Michael Walter's figure
can be grouped into just one shape. There are no big difference among these 3 shapes.
This group corresponds to Preston's "sub-elliptical" shape.
"longitudinal" can also be include as a "long-" type,, like "long-elliptical" and "long-subelliptical".
(2) "conical" and "pyriform" are two distinct group names. "conical" corresponds to Preston's
"oval", and "pyriform" corrsponds to Preston's "pyriform".
(3) "spherical" and "cylindrical" can be grouped into one "symmetric" group. This corresponds
to Preston's "spherical","elliptical", "long-elliptical" group.
(4) In conclusion, the result turns out to be similar to Preston's grouping.
In Preston's grouping, if "sub-elliptical" is renamed as "biconical"
both methods of classification are basically the same !!