Origami(Paper Folding) Solution

Origami Solution by Hisashi Abe (ref.1)

Hisashi Abe published a very unique Delian solution in a Japanese mathematical magazine in 1980. The method is now described in ref.1, published in 2003.
He uses a traditional Japanese paper folding technique , called "Origami".
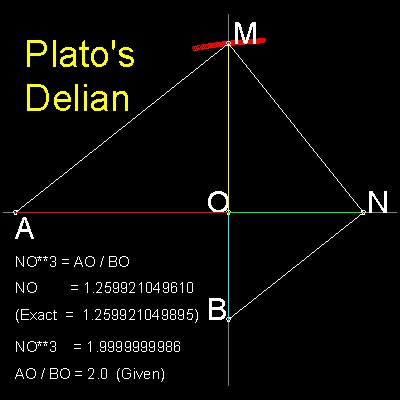
But first let us go back to Plato's Delian solution.

Plato's Delian Solution

The basis of this construction is that trianlges OAM, OMN, and ONB are similar. (angles AMN, and MNB are right angle.) Therefore if ON = a .OB Then OM = a2 .OB OA = a3 .OB Obviously if the ratio "a" is known, it is possible to construct these triangles starting from OB. Ref. 1 follows the reverse of the Plato's process,assuming that "a" is a given value, then show that the Delian solution can be obtained through the use of Origami's "mirror imaging" characteristic.

********** Plato_Delian_result_2.dwg *********

The reverse of Plato's process and Abe's equivalent "Origami" solution

Draw x ,y coordinate axis through "O". Let OP = 1 (unit length), OQ = a (arbitrary length) At Q , draw a line perpendicular to PQ. This line intersects x-axis at R. At R , draw a line perpendicular to QR. This line intersects y-axis at S.

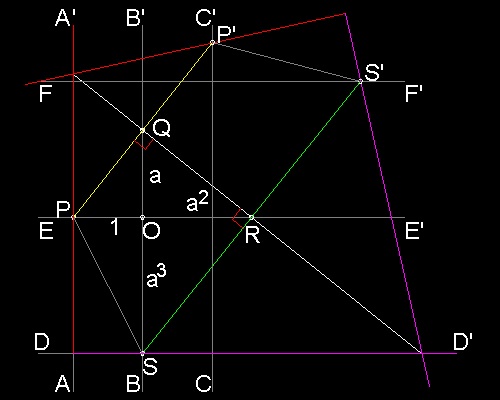
Draw a horizontal line DD' through S. Draw line FF' at the distance a3 from x-axis. Draw a vertical line AA' through P. Draw a line CC' at unit distance from y-axis. Using line QR as a mirror line,reflect line AA' and DD'. They intersects lines CC' and FF' at point P' , and S'. This means that line QR is found when points P,S fall on the lines CC' and FF', respectively, at the same time. In terms of Origami, this operation can be accomplished when the paper edges of AA' and DD' are moved so that points P & S touch lines CC' and FF', respectively.

You can see the process in animation.
********** Abe_Delian_model.dwg *********

To create this drawing and animation:
   Load Abe_Delian_model.lsp    (load "Abe_Delian_model")
  Then from command line, type Abe_Delian_model

Hisashi Abe's Delian solution

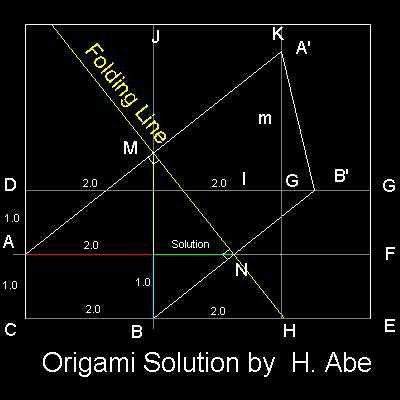
(1) Prepare a rectangular paper. All the corner angles must be exactly 90 degrees.
(2) Line AF, DG, BJ & HK are creases after folding along the lines.
(3) Distance between horizonral lines is 1 unit length.
(4) Distance between vertical lines is twice the unit value.
(5) Fold paper so that point A
falls on line HK and point B ,onto line DG.
Then distance ON is the cube root of 2.
Note:The extension of MN looks like intersecting AE at H
, but it is not the case.

You can see the process in animation.

********** Origami_Delian_desc.dwg *********

To create this drawing and animation:
   Load Abe_Delian.lsp    (load "Abe_Delian")
  Then from command line, type Abe_Delian
As usual, for a quick look , run test & test_2.

Example Run

What is required is a square or rectangle paper.
But here a rectangle graph paper is used .
In this example: OP = 2 inches, OS = 1 inch

Check the result against the exact values.
OR = 2^1/3 = 1.2599.., and OQ = 2^2/3 = 1.5874..
OR = between 1.25 ~ 1.3 and OQ = between 1.55 ~ 1.6
So in spite of a simple folding operation, precision is very good.

************* Abe_Delian_test.dwg ************

References

1. Abe, Hisashi: "Amazing Origami" , (in Japanese), 2003, ISBN 4-535-78409-4

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved .