Source of the contents for this section

History of the problem

Problem Definition:

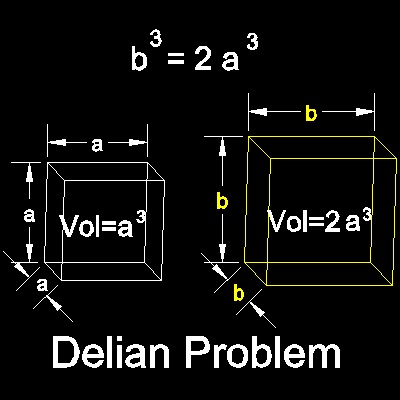
To construct the edge of a cube that is double the volume of a given cube

************ Delian_problem.dwg *************

Origin of the Problem :

The book "A History of Greek Mathematics" by Sir Thomas Heath, quotes one of the

prominent mathematician, Eratosthenes's comment.

"when the god proclaimed to the Delians by the oracle that, if they would get rid of a plague

they should construct an altar double of the existing one, their craftmen fell into great

perplexity in their efforts to discover how solid could be made double of a (similar) solid;

they therefore went to ask Plato about it, and he replied that the oracle meant, not that the god

wanted an altar of double the size, but that he wished, in setting the task, to shame the Greeks

for their neglect of mathematics and their contempt for geometry"

Rule of the Game ( Platonian Rule ) :

Tools allowed

Permitted use of these 2 tools

2. The construction of a circle with center at a given point and passing through a second given point.

3. The procedure must be a finite number of operations

Summary of Early Attempts:

Proof of impossiblility:

with ruler and compasses. But the first published proof was given by Frenchman, Pierre Wantzel (1814 - 1848), in 1837.

References:

1. Heath,Thomas L. :"History of Greek Mathematics Vol. I From Thales to Euclid" Dover 1981

2. Heath,Thomas L. :"A Manual of Greek Mathematics" Dover 1963 original 1931

3. Heath,Thomas L. :"A History of Greek Mathematics Vol. II" Dover 1981 original in 1921

4. Heath,Thomas L. :"The Works of Archimedes Dover" 2002 original in 1912

5. Knorr,Wilber Richard :"The Ancient Tradition of Geometric Problems" Dover 1993

6. Knorr,Wilber Richard :"The Textual Studies in Ancient and Medieval Geometry",Birkhauser, 1989

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved.