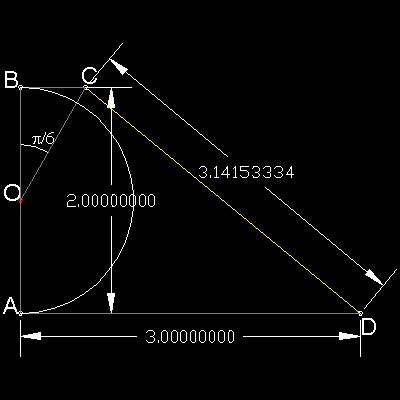
Kochansky published this result in 1685.

OA = OB = r, and AD = 3r
BC is paralllel to AD, and angle BOC = 30 degrees.
Then CD = 3.141533..
*************** Kochansky.dwg ***************
To create this drawing :
Load pi_construction.lsp (load "pi_construction")
Then from command line, type Kochansky
Jacob de Gelder (1765- 1848) published this result in 1849.
This is based on the approximation 355/113 = 3 + 42/(72 + 82).
This decimal portion is to be constructed.
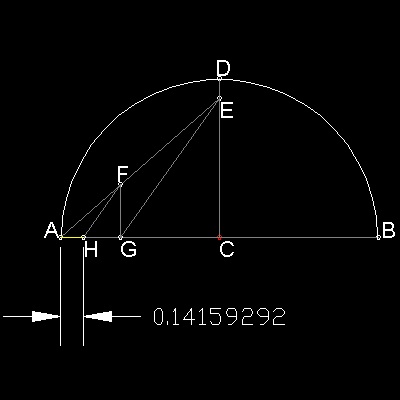
CD = 1, CE = 7/8, AF = 1/2
FG is parallel to CD, and HF is parallel to GE.
Then AH = 42/(72 + 82).
**************** Gelder.dwg *****************
To create this drawing :
Load pi_construction.lsp (load "pi_construction")
Then from command line, type Gelder
Hobson published this result in 1913. He constructed the approximate value of square root of pi,which is the true "circle squaring". p1/2 = 1.77245... His constructed length is 1.77246...,which is very,very close!!
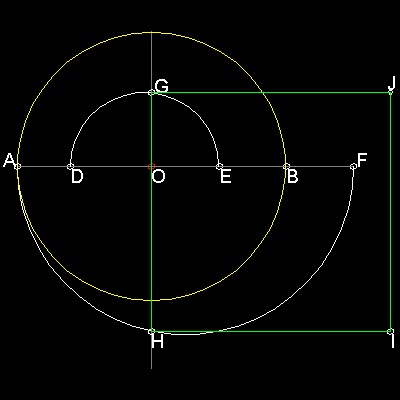
OA = 1.0, OD = 3/5, OF = 3/2, and OE = 1/2
Draw the semicircles DGE , AHF with DE and AF as diameters.
The perpendicular to AB through O intersects These semicircles at G & H.
Then GH = 1.77246...
**************** Hobson.dwg *****************
To create this drawing :
Load pi_construction.lsp (load "pi_construction")
Then from command line, type Hobson
More topics to be added.
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006