Origami(Paper Folding) Solution--Approximation

1. Create 355/113 exactly on a square paper( by Kazuo Haga )

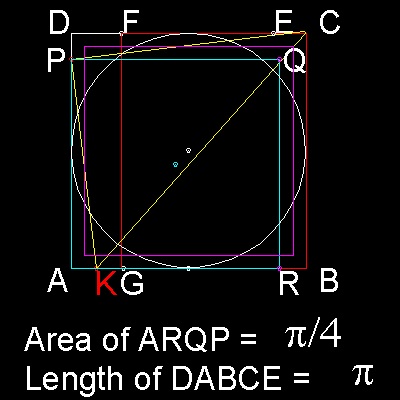
In the drawing below, ABCD is a square sheet of paper.

The circle squaring goes through 3 steps. 1. Find a point E on the side CD such that the length of DABCE = 355/113 exact. Use Haga's theorem repeatedly. 2. Make a rectangle with its area = p/4 (FGBC in color red) length FC = p/4 3. Make a square with its area = p/4 (PARQ in color cyan) point K is the mid point of AG. Point P is found by moving corner B using K as pivot until B touches line AD.(in yellow lines) AP is one side of the square. Note that crease line through K is slightly off the point C.

***** origami_circle_squarer_desc.dwg ******

Step 1: Find point "E"

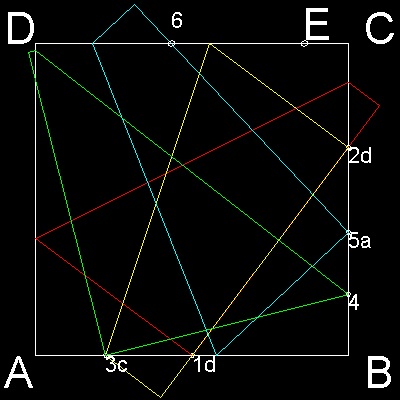
1. Move the corner point D to the mid point of AB ("1d"). Mark the point where CD crosses BC ("2d") This point is at the distance of 1/3 from point C. 2. Move the corner point D to point "2d". This creates point "3c". Distance between B and "3c" is 7/9 . 3. Move point C to "3c". This creates point "4", which is 16/81 from point B. Double this distance (32/81) and creates point "5a". 4. Move corner A to point "5a". This creates point "6" at 64/113 from point C. 5. Take 1/4 of this length from point C. This is point "E". The total length of DABCE is 355/113, which is a very good approximation of p. 355/113 = 3.14159292... p = 3.14159265...

******** Haga_circle_squaring_step_1.dwg ********

You can see the process in animation.

To create this drawing and animation:
   Load Haga_circle_sqr.lsp    (load "Haga_circle_sqr")
  Then from command line, type Haga_step_1

Step 2: Make a rectangle with its area = p/4

 
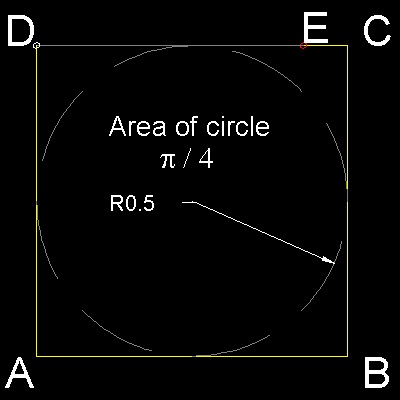
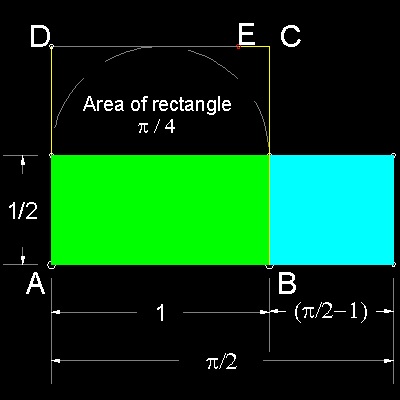
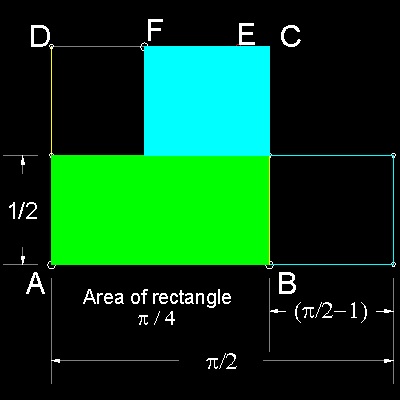
Haga_circle_squaring_step_2_0.dwg
 Area of a circle inscribing the square = p/4 .

Haga_circle_squaring_step_2_1.dwg 
 A rectangle , made up of 2 rectangles
 (green & cyan),   has the same area.

Haga_circle_squaring_step_2_2.dwg
 Let F be the mid point of DE.
 Since DE = 4 - p,
	FC = 1 - DE/2 = p/2 - 1
 So the rectangle in cyan color can be moved up 
 to align with FC.

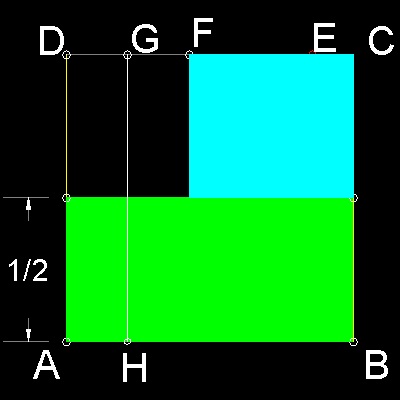
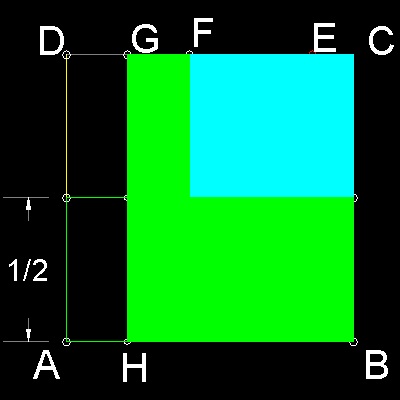
***** Haga_circle_squaring_step_2_3.dwg ***** ***** Haga_circle_squaring_step_2_4.dwg *****

Haga_circle_squaring_step_2_3.dwg Let G be the mid-point of DF, and GH be drawn parallel to DA . Haga_circle_squaring_step_2_4.dwg A part of green rectangle between DA and GH can be moved up to fill space between cyan rectangle and line GH. Now rectangle GHBC has the area = p/4 .

To create this drawing :
   Load Haga_circle_sqr.lsp    (load "Haga_circle_sqr")
  Then from command line, type Haga_step_2

Step 3: Make a square with its area = p/4

 
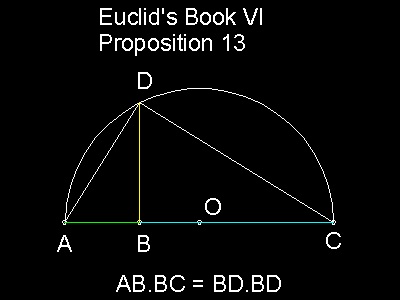
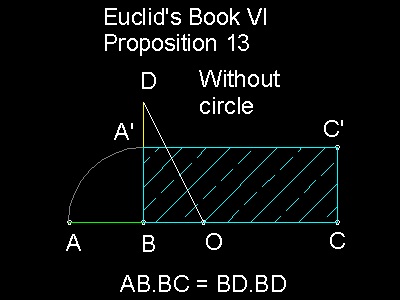
Euclid_prop_13.dwg
 Let AB, BC be the two given straight lines.
 Draw a semi circle ADC with diameter AC.
 Let BD be drawn from the point B at right angle to the line AC.
 Then  AB x BC = BD2

Euclid_prop_13_a.dwg
 Even when a semi-circle cannot be drawn by some reason, then if we let OB = OD,
 point D can be defined.
 This is exactly the case here.

 Note that OB = OD = (1/2)(AB + BC)

To create this drawing :
   Load Haga_circle_sqr.lsp    (load "Haga_circle_sqr")
  Then from command line, type Haga_step_3

References

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Feb 24, 2007

Copyright 2006 Takaya Iwamoto   .