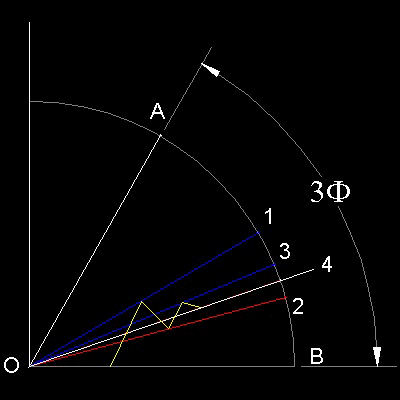
This approximate procedure is using the property of the following sum of the geometric series.
Sn= 1/4 + (1/4)2 + (1/4)3+ (1/4)4+ . . . + (1/4)n
As n increases, this series sum Sn approaches 1/3 .
The actual trisection process is using angle bisection repeatedly .
For example, 1/4 = 1/2 - 1/4, (1/4)2 = (1/4){(1/2) - (1/4)}, etc

Angle to be trisected is AOB.
n=1 ;bisect angle AOB (point 1)
n=2 ;bisect angle 1OB (point 2)--Angle 2OB = 1/4 now
n=3 ;bisect angle 1O2 (point 3)
n=4 ;bisect angle 3O2 (point 4)--Angle 4Ob = 1/4 + (1/4)2
n=5 ;bisect angle 3O4
n=6 ;bisect ... etc
You can see the process in animation.
****** approximation_series_tri_desc.dwg ******
To create this drawing and animation:
Load gen_sect.lsp (load "gen_sect")
Then from command line, type trisect_by_series
Animation files Creation: animation_series
This is credited to the 15-th century mathematician, Nikolas von Cusa, and the 16-th century mathematician, Willebrod Snellius.
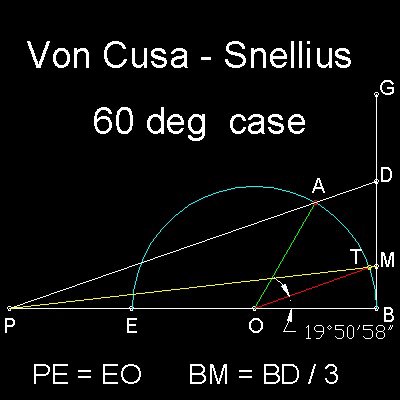
Draw a semi-cirlce OBE. Pick a point P on BE such that PE = EO.
Select a point "A" on the semi-circle. AOB is the angle to be trisected.
Erect a line GB perpendicular to EB at B.
Draw a line from P through A to intersect with GB at D.
Find a point M on line BD such that BM = BD/3 .
Connect P and M. This will intersect the semi_circle at point T.
Line segment TO is the approximate trisecting line for angle AOB.
In 60 degrees case ,the error is about 9'02",which is very very good !!
******** VonCusa_Snellius_desc.dwg *********
To create this drawing and animation:
Load VonCusa.lsp (load "VonCusa")
Then from command line, type VonCusa
In 1525 Albrecht Dürer published the following simple and very accurate approximation for angle trisection.

Angle to be trisected is AOB.
Let QA = QB = 1, and M1 & M2 divide line segment AB into three equal parts.
At M1 & M2, erect lines perpendicular to AB to intersect the arc C1 & C2 .
Find point D such that AD = AC1
Find point E such that DE = M1D/3
Draw a circle with center at A and radius AE. This circle intersect the arc at point T.
Line TO is the approximate trisetor of angle AOB
************** Durer_desc.dwg ***************
To create this drawing and animation:
Load Durer.lsp (load "Durer")
Then from command line, type Durer
This simple approximation procedure was dicovered by Karajordanoff in 1928.
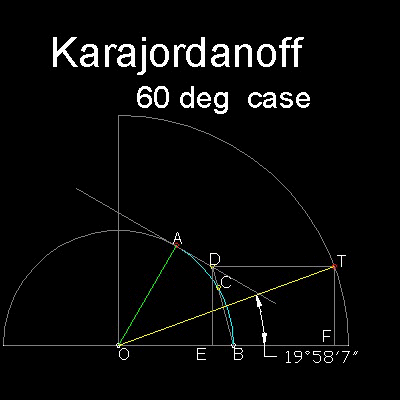
Angle to be trisected is AOB.
two circles of radii 1 and 2 are drawn abou the angle AOB.
Extend a line from B passing through point C, a midchord point of AB.
Draw a tangent line at point A.
This tangent and line BC intersects at point D
Draw a line DT parallel to OB. T is the point this line intersects the arc AB.
Line TO is the approximate trisector.
Trisecting error for the given angle 60 degrees is about 2 minutes.
********** Karajordanoff_desc.dwg ***********
To create this drawing and animation:
Load Karajordanoff.lsp (load "Karajordanoff")
Then from command line, type Karajordanoff
This approximation method was published by Kopf in 1919, and later it was refined by Perron and d'Ocagne.
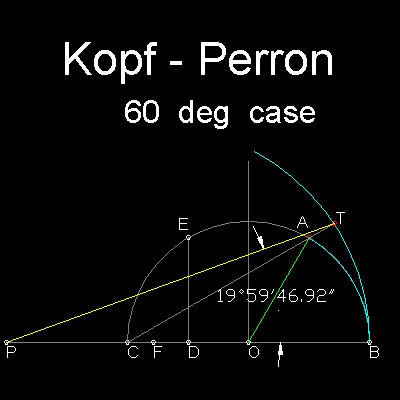
Angle to be trisected is AOB.
Point5s A,B & C are on the unit circle. D is the mid point of OC, and ED is vertical to OC.
POint F is set such that DF is 1/3 of line length ED, and CP = CO= 1.
Draw an arc with its center at point F and radius equal to FB.
Line CA intersects this arc at point T.
Line TP is the approximate trisector.
Trisecting error for the given angle 60 degrees is about 13 minutes.
*********** Kopf-Perron_desc.dwg ************
To create this drawing :
Load Kopf_Perron.lsp (load "Kopf_Perron")
Then from command line, type Kopf_Perron
This extremely simple method that is surprisingly accurate for smalll angles is given by d'Ocagne.(published in 1934)
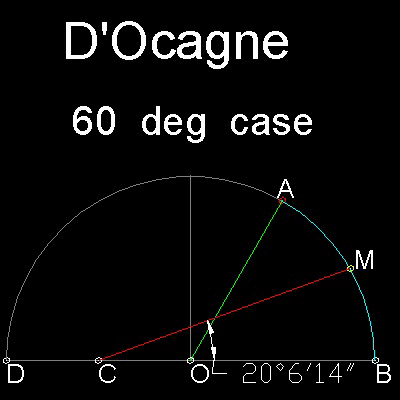
Angle to be trisected is AOB.
Points A & B are on the unit circle.
Point C is the mid point of the unit radius.
Point M is the midpoint of the chord AB
The line CM is approximate trisecting line.
In this example case (Angle AOB = 60 degrees), the error is only 6'14",which is a very good approximation.
************ D'Ocagne_desc.dwg *************
To create this drawing :
Load D'Ocagne.lsp (load "D'Ocagne")
Then from command line, type Docagne
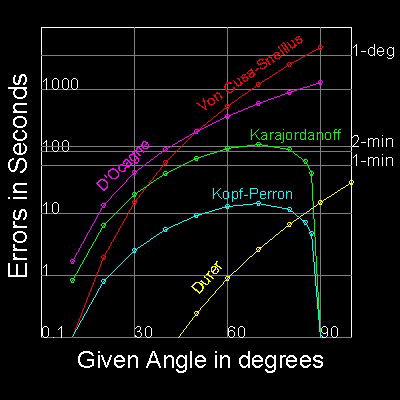
The errors of 5 approximation methods are shown in the graph.
Notice that Y-axis is in logarithm scale because the error values(in seconds) range from less than 0.01 to 5000.
Values less than 0.1 are all set to 0.1 for display purpose.
************ compare_errors.dwg *************
To create this drawing :
Load compare_errors.lsp (load "compare_errors")
Then from command line, type compare_errors
1. Yates,Robert Carl : "The Trisection problem" , pp.47-56
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.