Go to Fun_Math Content Table
Trisecting an Angle
Classical solutions by Insertion (Neusis or Verging) method
1. Archimedes' Insertion Method #1
Archimedes' Solution is shown in the figure shown below.
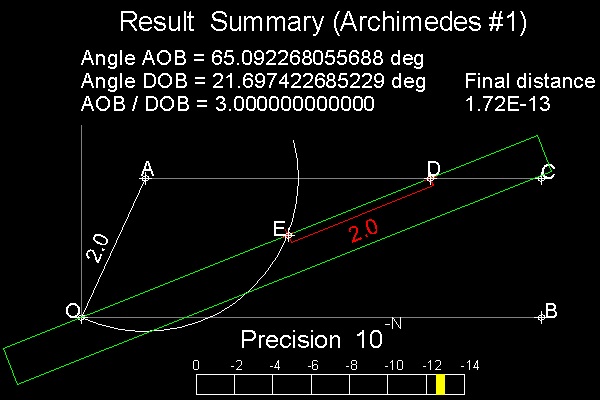 Steps of trisection:
Steps of trisection:
1. Draw a circle with a radius=2
Define a point A on this circle.
Angle AOB is the angle to be trisected.
Draw a line AC parallel to line OB.
2. Prepare a ruler (in color green)
with marked point E & D (distance 2.0 apart)
3. Move the ruler in such a way the edge passes
through point O and point E comes on the circle.
4. Keep moving the ruler until point D touches line AC.
Objective here is to make the distance from point D to line AC as small as possible.
If the point D is exactly on line AC (distance from D to AC is zero)
,the trisection is done. But that is not possible with finite
number of operations.
Try this to make sure you understand the above statement.
Draw a line and try to locate a point on the line(without object snap ! Remember O,E & D are one line).
************************* trisect_Archimedes_1.dwg *****************
Computing and display Scheme
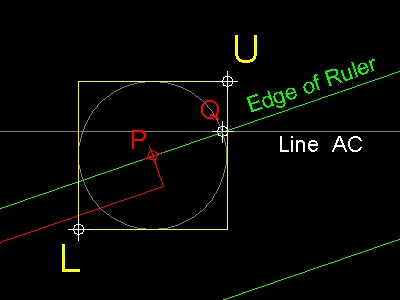 In order to make the point D as close as possible to line AC, the computer screen must be zoomed automatically
so that the movement of the mouse corresponds to finer adjustment. The idea the author adopted is as follows:
In order to make the point D as close as possible to line AC, the computer screen must be zoomed automatically
so that the movement of the mouse corresponds to finer adjustment. The idea the author adopted is as follows:
1. split the screen into 2 windows, the global view window and the zoomed view window.
2. everytime the mouse position (P) is decided by left click, a new set of window limits(L and U in the picture)
is computed based on the radius PQ,where Q is the intersection of line AC and the edge of the ruler.
And zooming is performed according to this set of limit positions.
3. to help see the current precision during execution, a "precision bar" is displayed on the global
window to show the distance PQ.
The process is continued until the prespecified number ( 1.e-10 ) is reached .
*************** auto_zoom.dwg **************
 The automatic zooming scheme described above is the technique the author uses to solve the general non-linear
problems by graphic mean. The majority of the problems in the three famous problems in Greek mathematics can be
solved by using this technique.
The automatic zooming scheme described above is the technique the author uses to solve the general non-linear
problems by graphic mean. The majority of the problems in the three famous problems in Greek mathematics can be
solved by using this technique.
************************* neusis_1_zoom.dwg *******************
You can see the process in animation.
To create this drawing and animation:
Load neusis.lsp (load "neusis")
Then from command line, type neusis_1
2. Pappus' Insertion method
Pappus' Solution is shown in the figure shown below.
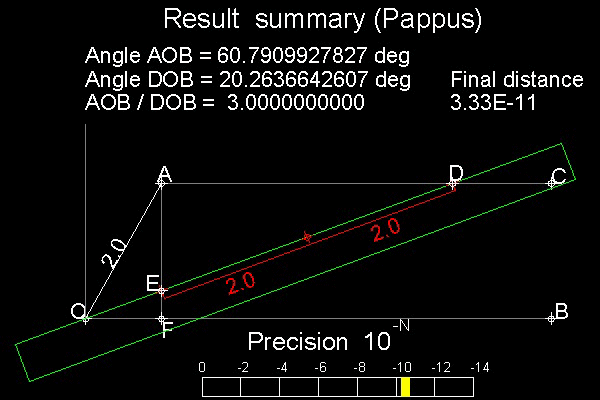 Steps of trisection:
Steps of trisection:
1. Draw a circle with a radius=2
Define a point A on this circle.
Angle AOB is the angle to be trisected.
Draw a line AC parallel to line OB.
Draw a line AF perpendiculat to line OB.
2. Prepare a ruler (in color green)
with marked point E & D (distance 2 x 2.0 apart)
3. Move the ruler in such a way the edge passes
through point O and point E comes on line AF.
4. Keep moving the ruler until point D touches line AC.
Objective here again is to make the distance from point D to line AC as small as possible.
************************* trisect_Pappus_1.dwg *******************
You can see the process in animation.animation
To create this drawing and animation:
Load neusis.lsp (load "neusis")
Then from command line, type neusis_2
3. Archimedes' Insertion Method #2
Archimedes' Solution is shown in the figure shown below.
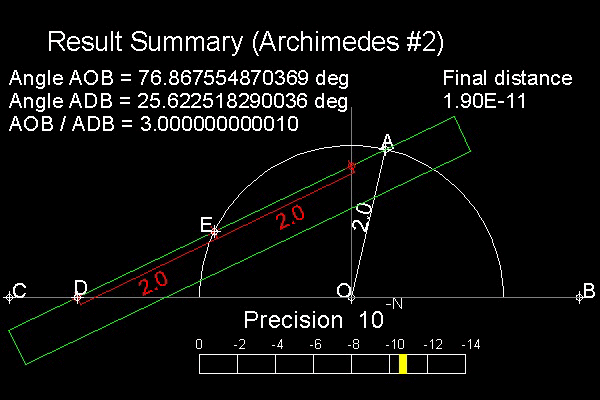 Steps of trisection:
Steps of trisection:
1. Draw a circle with a radius=2
Define a point A on this circle.
Angle AOB is the angle to be trisected.
2. Prepare a ruler (in color green)
with marked point E & D (distance 2.0 apart)
3. Move the ruler in such a way the edge passes
through point A and point E comes on the circle.
4. Keep moving the ruler until point D touches line BC.
Objective here again is to make the distance from point D to line BC as small as possible.
The same ruler used for Pappus is used here to show the similarity of the approach (upside down).
************************* trisect_Archimedes_2.dwg *******************
You can see the process in animation.animation
To create this drawing and animation:
Load neusis.lsp (load "neusis")
Then from command line, type neusis_3
4. Equivalent Cubic equation
Trisection equation is a cubic polynomial equation without quadratic( X 2) term.
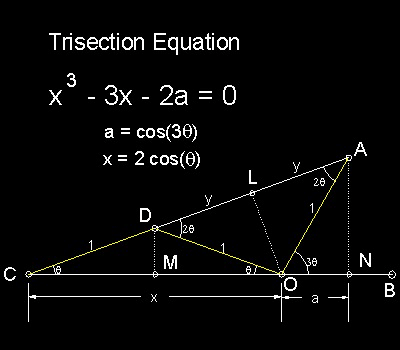 This means that the angle trisection is equivalent to draw a line of cubic root using only the unmarked ruler and compass,
which has been proved impossible first by Wantzel.
This means that the angle trisection is equivalent to draw a line of cubic root using only the unmarked ruler and compass,
which has been proved impossible first by Wantzel.
******** trisection_equation_desc.dwg *********
Derivation:
Algebraic Formulation:
Since three triangles CDM, COL and CAN are similar. CM/CD = CL/CO = CN/CA.
So x/2 = (1 + y)/x = (x + a)/(1 + 2y)
which gives ---> x2 = 2 + 2y and 1 + 2y = 2(x + a)/x
Eliminating y from these two equations, we obtain x 2 - 1 = 2(x + a)/x or
x 3 - 3x - 2a = 0
where x = 2cos(q) and a = cos(3q)
References
1. Yates, Robert Carl : "The Trisection problem"
Go to
Fun_Math Content Table
Trisecting an Angle
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.
.
 Steps of trisection:
Steps of trisection:
 In order to make the point D as close as possible to line AC, the computer screen must be zoomed automatically
so that the movement of the mouse corresponds to finer adjustment. The idea the author adopted is as follows:
In order to make the point D as close as possible to line AC, the computer screen must be zoomed automatically
so that the movement of the mouse corresponds to finer adjustment. The idea the author adopted is as follows:
 The automatic zooming scheme described above is the technique the author uses to solve the general non-linear
problems by graphic mean. The majority of the problems in the three famous problems in Greek mathematics can be
solved by using this technique.
The automatic zooming scheme described above is the technique the author uses to solve the general non-linear
problems by graphic mean. The majority of the problems in the three famous problems in Greek mathematics can be
solved by using this technique.
 Steps of trisection:
Steps of trisection:
 Steps of trisection:
Steps of trisection:
 This means that the angle trisection is equivalent to draw a line of cubic root using only the unmarked ruler and compass,
which has been proved impossible first by Wantzel.
This means that the angle trisection is equivalent to draw a line of cubic root using only the unmarked ruler and compass,
which has been proved impossible first by Wantzel.