History of the Problems

History of the Problems HIstory of the Problem

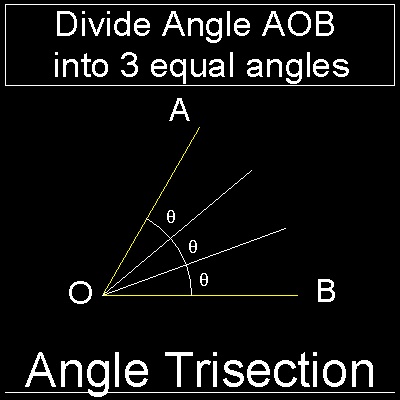
Go to Fun_Math Content Table Trisecting an Angle

Source of the contents for this section

Most of the contents of this section come from "The Trisection Problem" (ref. 1) by Yates. Actually this book is the reason why I have decided to open a public web site for demonstrating geometry in dynamic fashion using CAD software.I have added topics on Origami(taken from ref. 5 ), Maclaurin's method (from ref. 3), and discussion of equivalence of three methods(Tomahawk, Carpenter's square and Origami).
So for those who want to learn seriously about this topic, purchase of ref.1 through used bookstore is highly recommended.

History of the problem

Problem Definition:

To divide an "ARBITRARY" angle into three equal angles.

It is important to note that angles like 45,72, 90 & 180 degrees
can be divided into 3 equal parts by using only compass and ruler.

******** angle_trisection_problem.dwg ********

Origin of the Problem :

The origin of this problem is not clear even among the experts on this subject.

The bisection of any angle can be done easily with compass and straight-edge, but if the number

of division becomes three, Greek mathematicians encountered a difficulty.

Rule of the Game ( Platonian Rule ) :

Tools allowed

the compasses and unmarked straight-edge

Permitted use of these 2 tools

1. The drawing of a straight line of indefinite length through two given points.

2. The construction of a circle with center at a given point and passing through a second given point.

Summary of Early Attempts:

Greek mathematicians ,although they could not prove it, knew that Angle Trisection is not possible because their trisection attempts were all violation of the Platonian Rule. Quadratrix of Hippias, Conchoid of Nicomedes, and verging solution by Archimedes are their typical answers.

Proof of the impossibility:

Carl Friedrich Gauss (1777 - 1855) had stated without proof that the problems of trisecting an angle and doubling a cube cannot be solved

with ruler and compasses. But the first published proof was given by Frenchman, Pierre Wantzel (1814 - 1848), in 1837.

Comments on the References:

A very good introduction is the following web site.
Trisecting an angle

If you are looking for a book, ref(1) is the best choice. It is easy to read with brief and clear explanation.

The problem is that there are only a limited number of used books available on the market.

1. Yates,Robert C.:"The Trisection problem",first published in 1942.

2. Dudley,Underwood :"The Trisectors" The Mathematical Association of America,1994.

3. Ogilvy,Stanley C. :"Excursions in Geometry" Dover,first published in 1969

4. Dorrie, Heinrich :"100 Great Problems of ELementary Mathematics-Their History and solution", Dover 1965

The original was published in 1932.

5. Abe, Hisashi : "Amazing Origami"(In Japanese)

Go to Fun_Math Content Table Trisecting an Angle

All questions/complaints/suggestions should be sent to takaya.iwamoto@comcast.net

Last Updated July 9-th, 2006