Mechnical Links

Go to Fun_Math Content Table Trisecting an Angle

Trisection using Origami(Paper Folding)

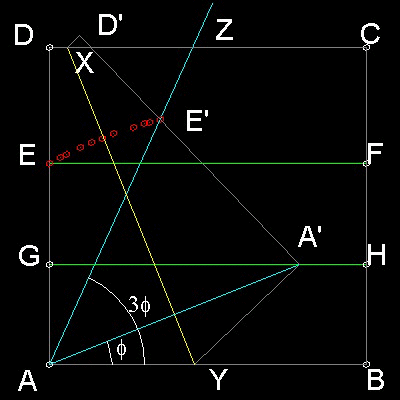
Only a piece of square paper is required for trisecting a given angle,using Origami technic. Hisashi Abe invented this idea and published in July, 1980 edition of the Japanese journal "Suugaku Seminar"(Mathematics Seminar).

Trisection procedures

1. Angle to be trisected is ZAB. Move the edge AD to the right and mark line AZ.

2. Move the edge DC and mark line EF paralell to AB.

3. Move the edge AB on EF and fold to mark line GH.

4. Grab the corner point "A" and move along line GH until point "E" touches line AZ,then fold the paper to mark line XY.

5. The final positions of "A" and "E" are called "A'" and "E'". Line AA' trisects angle ZAB.

You can see the process in animation.
******** origami_tri_desc.dwg ********

To create this drawing and animation:
   Load Abe_H.lsp    (load "Abe_H")
  Then from command line, type Abe_hisashi
  For a quick look at the program, type abe_h1 & abe_h2

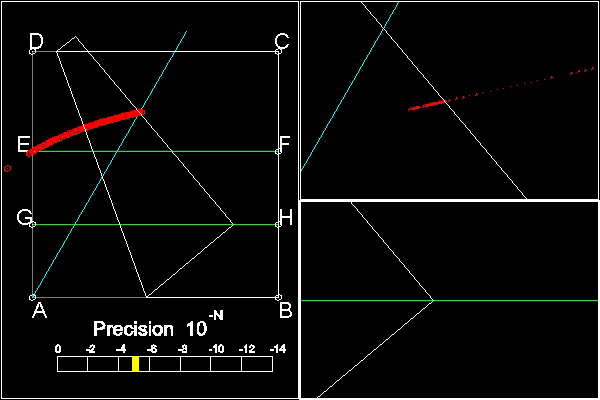
Typical 3 viewports are shown below:

Left viewport:global picture showing the level of precision

Upper Right Viewport: red point show where point E' is .This must come on the Cyan line.

Lower Right Viewport: Point A' moves along the green line GH. Cursor must be within this viewport.

The program execution is done by moving point A' in the Lower Right Viewport so that point E' will come closer on cyan colored line. The distance from the point E' normal to cyan colored line is shown in the precision bar in the left viewport.This snap shot is at the stage when the distance is in the order of 10 to the minus 5 ( = 10^-5 ).
******** Abe_Hisashi_60_deg.dwg ********

Example Run: 60 degrees case:

******** origami_60_deg_case.dwg ********

Comparison with other 2 methods

When Abe_Hisashi's method is compared with "tomahawk" and "carpenter's_square", it becomes clear that ,from the geometrical point of view, they are all based on the same principle.
Three methods are run for 60 degrees case, and they are all displayed at the same reference position, with the same scale.

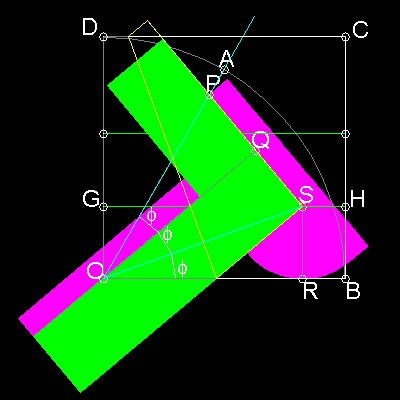
******** compare_three_methods.dwg ********

To create this drawing and animation:
Load Abe_H.lsp (load "Abe_H")
Then from command line, type three_methods
In order to run this program you also need the following drawing files.
******** comparison_carpenter's_square.dwg ********
******** comparison_tomahawk_bare.dwg ********
******** comparison_origami_bare.dwg ********

Analytical Curve to find the point "P"

If the reader look at the first drawing in this section, one will notice immediately that there seems to be a curve passing through point E and P.
The author tried to derive the formula using the distance BH as a parameter m.
The result is as follows:
(x/m)² = {(1 + y/m) (y/m - 2)²} / (3 - y/m)
where
the origin of the coordinate is point "O"
X - axis is OB, and Y - axis is OD

In the drawing ,let OP = OS = l and angle SON = (1/3)angle PON
In the triangle SON, l*sin(q) = m. Then l = m /sin(q)
In the triangle POM, x = l*cos(3q) = m*cos(3q)/sin(q) ------(1)
and y = l*sin(3q) = m*sin(3q)/sin(q) = m*(3sin(q) - 4sin³(q))/sin(q)
=(3 - 4sin²(q)*m = (4cos²(q) - 1)*m
Therefore,4cos²(q) - 1 = y/m, or cos²(q) = (1/4)(1+y/m) ------(2)
From (1) , x²sin²(q) = m²cos²(q)cos²(3q)
= m²cos²(q)(4cos²(q) - 3)²
******** origami_curve.dwg ********
Using the relations between cos²(q) and (y/m);
1 - cos²(q) = (1/4)(3 - y/m)
cos²(q) = (1/4)(1 + y/m)
4cos²(q) - 3 = y/m - 2
And finally ,
x² = m²{(1 + y/m) (y/m - 2)²} / (3 - y/m)

Trisection Example using "origami_curve"

Here is an example of angle trisection using this curve.

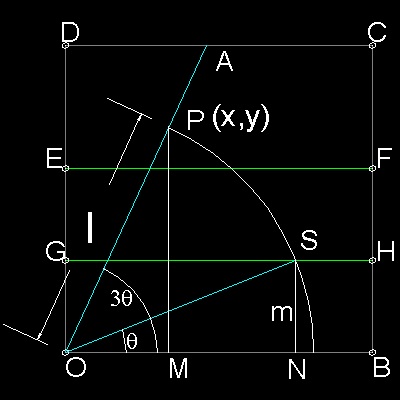
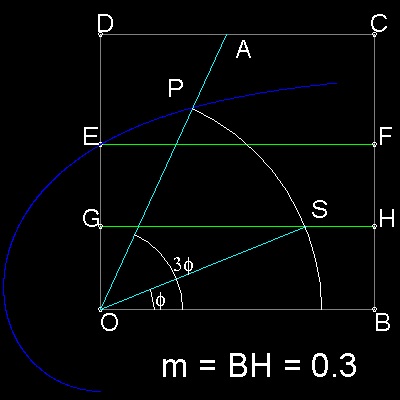
step (1): Pick a point "A" to define an angle to be trisected.
step (2): draw a "origami_curve", with m=0.3(arbitrarily chosen, but must be equal to BH length)
step (3): Find an intersection point "P" between OA and this curve.
step (4): Draw a circle with its center at "O" and radius OP.
step (5): This circle cuts line GH at point S.
step (6): line OS trisects angle AOB.
******** origami_curve_trisection.dwg ********

To create this drawing and animation:
Load Abet.lsp (load "Abet")
Then from command line, type Abe_4

References

1. Hisashi Abe:"すごいぞ折り紙" Published in Japanese , 2003. ISBN4-535-78409-4
Hisashi Abe: Published in Japanese--Amazon.com link

Go to Fun_Math Content Table Trisecting an Angle

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006