Topics from Lines and Circles
List of animations posted on this page.(Click the text to watch animation.)Use browser's "Back" button to come back to this page.
1. Conics as Envelopes of Lines
Conics as envelope of lines
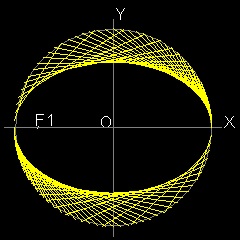
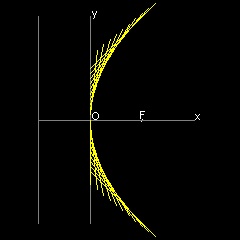
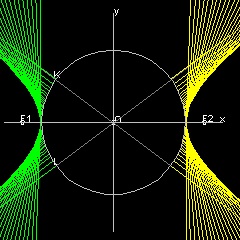
See ellipse as line envelope See parabola as line envelope See hyperbola as line envelope
Conics by drafting triangle
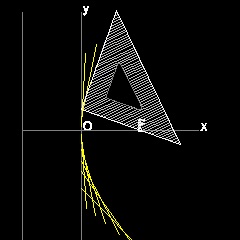
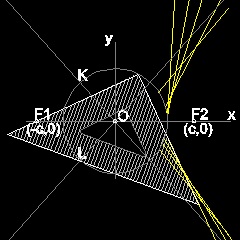
See ellipse by drafting triangle See parabola by drafting angle See hyperbola by drafting angle
Conics by paper folding
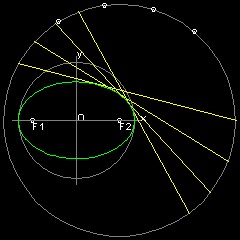
See ellipse by folding paper See parabola by folding paper See hyperbola by folding paper
For details, go to Ellipse ,Parabola and Hyperbola .
2. Cycloid, Epi & Hypo-cycloid as Envelopes of Lines
Cycloid
-------See cycloid_by_line envelope #0 -------See cycloid_by_line envelope #1 -------See cycloid_by_line envelope #2
For details, go to Cycloid,Epi & Hypo-cycloid as Envelopes of Lines
Epi-cycloid

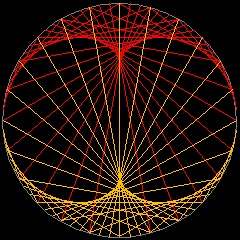
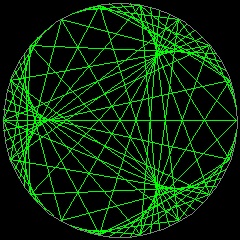
See Cardioid as line envelope See Nephroid as line envelope See Cremona as line envelope
For details, go to Epicycloid
Hypo-cycloid

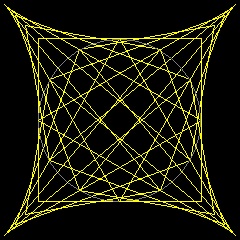

See Deltoid as line envelope See Astroid as line envelope See 6-cusped hypocycloid
For details, go to
Hypocycloid
Table of Contents
1. Conics by Envelope
The Conics (Ellipse, Parabola & Hyperbola) was invented by a Greek mathematician, Menaechmus (about 380 BC - about 320 BC) , tutor to Alexander the Great , in an attempt to solve "Delian Problem or Duplicating the Cube", which is one of the "Three Famous Problems" in Greek mathematics.Further studies were done by Apollonius of Perga (about 262 BC - about 190 BC).
There are many excellent references on this subject, and the ones the author could purchase via internet are listed in the reference section at the bottom of this page.
1.1 Ellipse
Envelope of lines
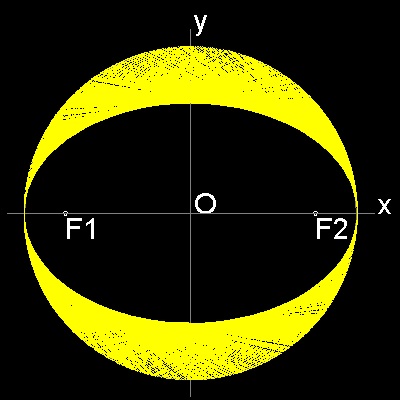
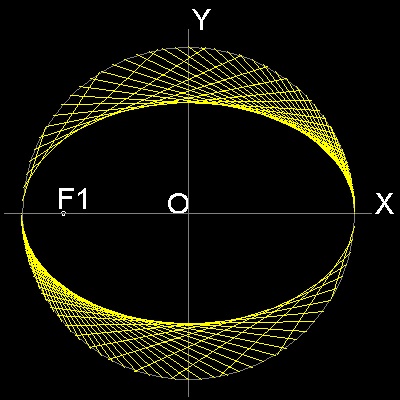
************* ellipse_manual_2.dwg *************
**************** ellipse_auto.dwg ****************
You can see the process in animation.
To create this drawing and animation:
Load conics_by_line.lsp (load "conics_by_line")
Then from command line, type ellipse_auto
To create ellipse_manual_2.dwg, type ellipse_manual_2 in command line window.
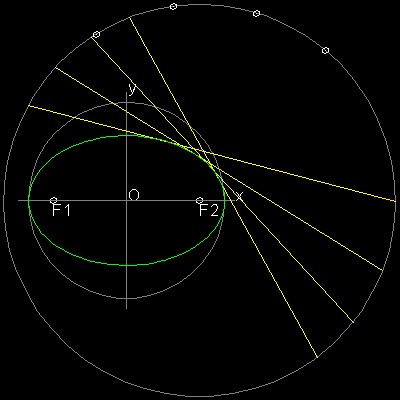
Description of ellipse
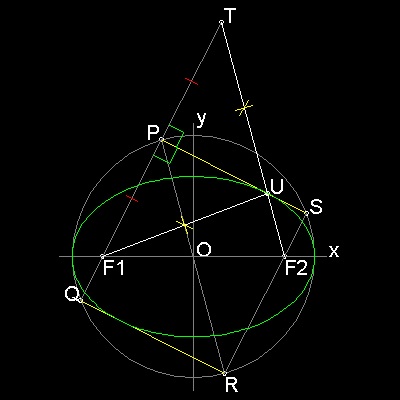
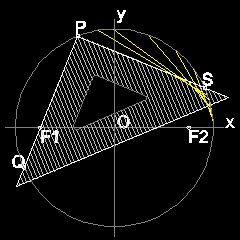
Draw a circle with radius = a. Select a point F1 with distance c from O. From a point P on the circle ,draw a line through F1 to Q on the circle. Draw a line PS perpendicualr to PQ. Make a rectangle PSRQ. It cuts x-asix at F2. Extend line F1P and make point T such taht F1P = PT Connect T-F2, This intersects PS at U. Since PQ is parallel to SR, triangles OPF1 is congruent to trianlge ORF2. Since trainlges UPF1 and UPT are congruent, F1U = UT. Therefore F2 is (c 0), and UF1 + UF2 = UF2 + UT = PR = 2a (constant) So the point U is on the ellipse with foci F1,F2. and also tangent to the curve at U. Envelope of many lines drawn like "PS" ,"QR" will make an ellipse as shown above.To create this drawing :
Load conics_by_line.lsp (load "conics_by_line")
Then from command line, type ellipse_model
*************** ellipse_model.dwg ***************
Using a drafting triangle
Using the property that points P,Q,& S are on the circle,and angle SPQ is a right angle, line PS can be drawn by using a drafting triangle as follows.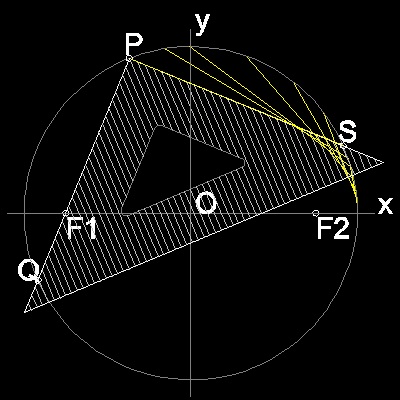 You can see the process in animation.
You can see the process in animation.
To create this drawing and animation:
Load conics_by_line.lsp (load "conics_by_line")
Then from command line, type ellipse_by_triangle
************ ellipse_by_triangle.dwg ************
Folding a cicular paper
It was shown that point T is on the circle with its center at F2 and radius 2a.When that circle is drawn , it becomes clear that line PS can also be a part of the line VW,
which is created as a crease line when a circular paper is folded so that point T falls on point F1.
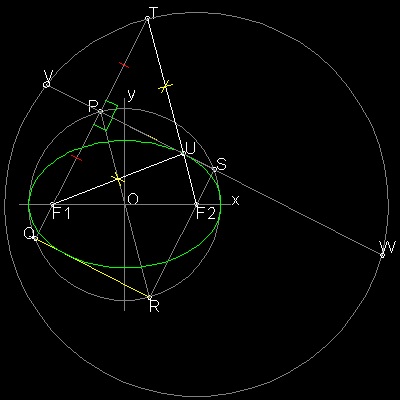
To create this drawing :
Load conics_by_line.lsp (load "conics_by_line")
Then from command line, type ellipse_model
Answer "Yes" to "Want to continue ?" prompt.
************** ellipse_model_2.dwg **************
 You can see the process in animation.
You can see the process in animation.
To create this drawing and animation:
Load conics_by_line.lsp (load "conics_by_line")
Then from command line, type ellipse_by_folding
************* ellipse_by_folding.dwg *************
1.2 Parabola
Envelope of lines
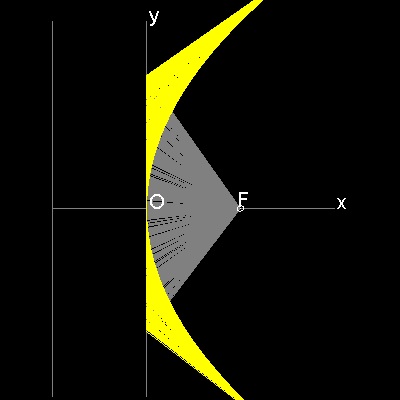
************* parabola_manual_2.dwg *************
**************** parabola_line.dwg ****************
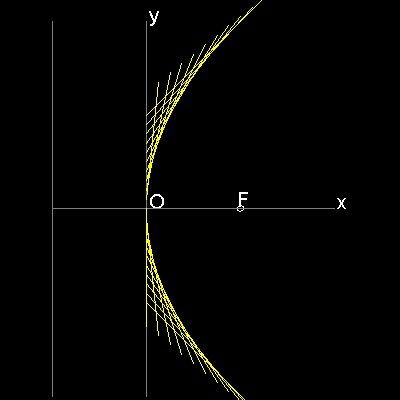
You can see the process in animation.
To create this drawing and animation:
Load conics_by_line.lsp (load "conics_by_line")
Then from command line, type parabola_auto
To create ellipse_manual_2.dwg, type ellipse_manual_2 in command line window.
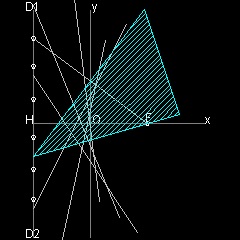
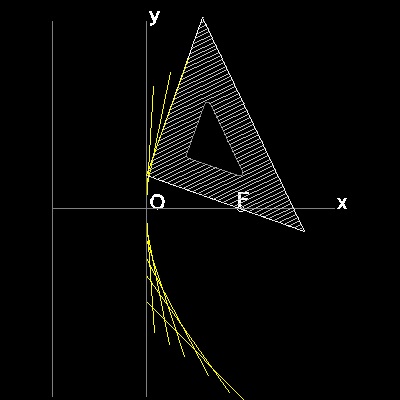
Description of parabola
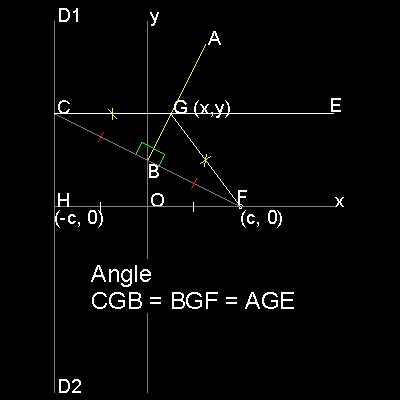
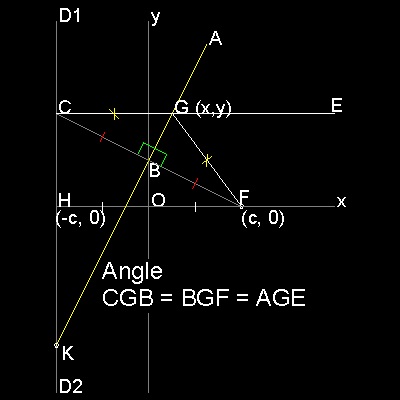
F is a Focus (c, 0), and line D1 D2 is parallel to y axis with distance c from the origin O.(called Directrix) B is a point on y-axis. FB intersects with directrix at C. Line AB is perpendicular to line FC at B. Draw a line from C parallel to x-axis, and this intersects AB at G. Then GC = GF -->definition of parabola Furthermore, angle CGB = BGF = AGE.-->angle bisector of EGF is normal to AB So point G is not only a point on the parabola,but line AB touches this parabola at point G. Consequently envelopes of lines like AB will form a parabola.
To create this drawing :
Load conics_by_line.lsp (load "conics_by_line")
Then from command line, type parabola_model
*************** parabola_model.dwg ***************
Using a triangle
Using the property that points B is on y-axis,and angle ABF is a right angle, line AB can be drawn by using a drafting triangle as follows.
 You can see the process in animation.
You can see the process in animation.
To create this drawing and animation:
Load conics_by_line.lsp (load "conics_by_line")
Then from command line, type parabola_by_triangle
************ parabola_by_triangle.dwg ************
Folding a paper
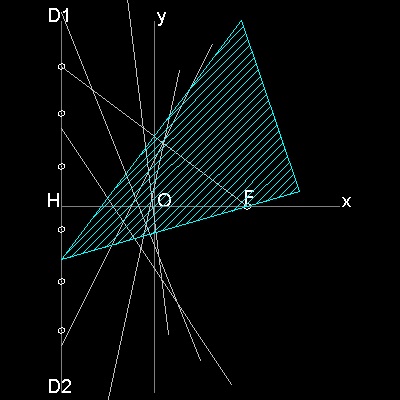
In the model drawing below, point C on directrix and Focus F are symmetric with respect to line AB.So line AB is created by a crease on the paper when a paper is folded such that a point on directrix falls on the Focus F.
Note here that directrix D1 D2 is considered as an arc of a circle with its center at infinity on x-axis.
To create this drawing :
Load conics_by_line.lsp (load "conics_by_line")
Then from command line, type parabola_model
The add line BK manually.
************** parabola_model_2.dwg **************
 You can see the process in animation.
You can see the process in animation.
To create this drawing and animation:
Load conics_by_line.lsp (load "conics_by_line")
Then from command line, type parabola_by_folding
************* parabola_by_folding.dwg *************
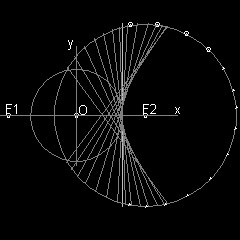
1.3 Hyperbola
Envelope of lines
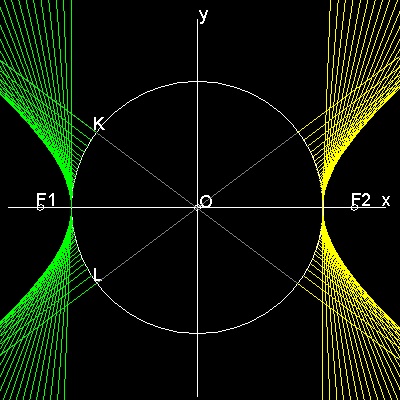
*********** hyperbola_manual_2.dwg ***********
************** hyperbola_auto.dwg **************
You can see the process in animation.
To create this drawing and animation:
Load conics_by_line.lsp (load "conics_by_line")
Then from command line, type hyperbola_auto
To create hyperbola_manual_2.dwg, type hyperbola_manual_2 in command line window.
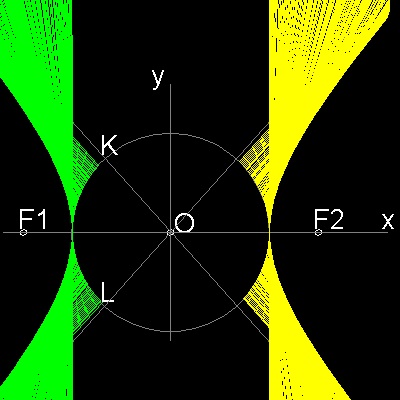
Description of hyperbola
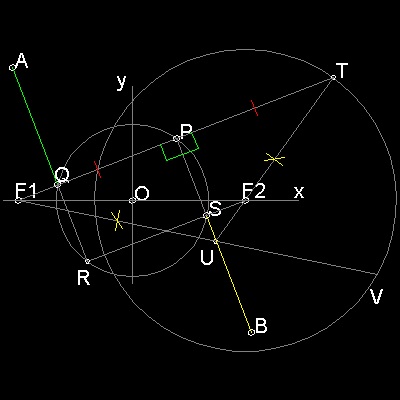
Draw a circle with radius = a. Select points F1,F2 outside of this circle with distance c from O. From a point P on the circle ,draw a line through F1 to Q on the circle. Draw lines PB and RA perpendicualr to PQ.They intersect the circle at R & S. PSRQ is a rectangle. Extention of RS goes through F2 due to symmetry. Extend line F1P and make point T such that F1P = PT Connect T-F2, This intersects PS at U. Since triangles UPF1 and UPT are congruent, F1U = UT Therefore UF1 - UF2 = UT - UF2 = F2T = 2a (constant). So the point U is on the hyperbola with foci F1,F2. Furthermore since angles PUF1 = PUT = BUV, line BP is a tangent line to this hyperbola at U.
To create this drawing :
Load conics_by_line.lsp (load "conics_by_line")
Then from command line, type hyperbola_model
************* hyperbola_model.dwg *************
Using a triangle
Using the property that points P,Q,& S are on the circle,and angle SPQ is a right angle, line PS can be drawn by using a drafting triangle as follows.
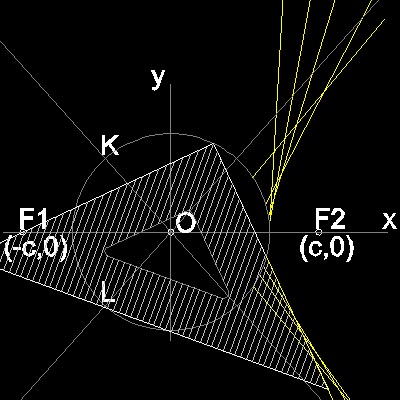 You can see the process in animation.
You can see the process in animation.
To create this drawing and animation:
Load conics_by_line.lsp (load "conics_by_line")
Then from command line, type hyperbola_by_triangle
************ hyperbola_by_triangle.dwg ************
Folding a cicular paper
It was shown that point T is on the circle with its center at F2 and radius 2a.When that circle is drawn , it becomes clear that line PS can also be a part of the line VW,
which is created as a crease line when a circular paper is folded so that point T falls on point F1.
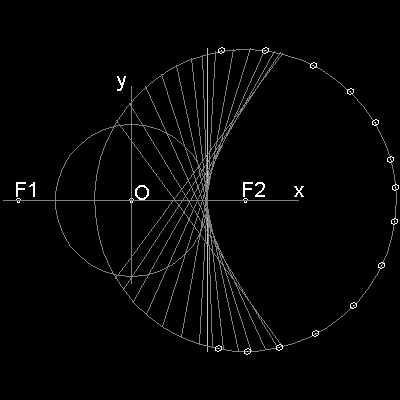 You can see the process in animation.
You can see the process in animation.
To create this drawing and animation:
Load conics_by_line.lsp (load "conics_by_line")
Then from command line, type hyperbola_by_folding
********** hyperbola_by_folding.dwg **********
2. Cycloid, Epi & Hypo-cycloid as Envelopes of Lines
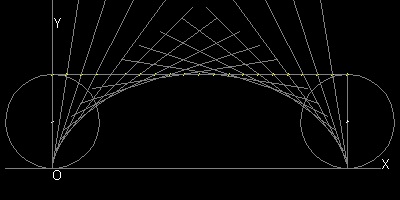
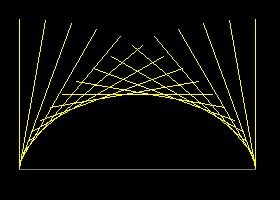
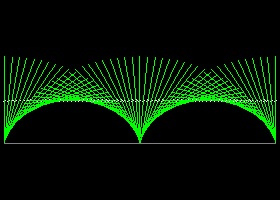
2.1 Cycloid
Envelope of lines
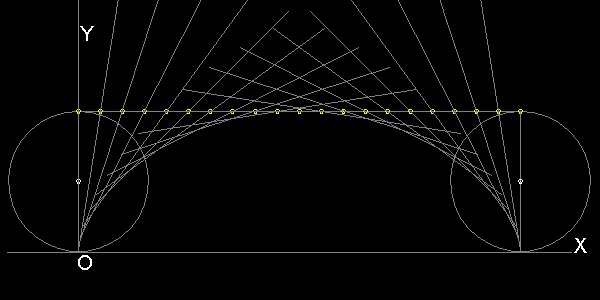
******************* cycloid_by_line_envelope.dwg ************************

******************* cycloid_by_line_envelope_2.dwg *********************
You can see the process in animation.
To create this drawing and animation:
Load cycloid1.lsp (load "cycloid1")
Then from command line, type draw_cycloid_by_line
1-st example: no. of division = 20
2-nd example: no. of division = 200, and layer2 (yellow colored nodes) is hidden.
Description of cycloid
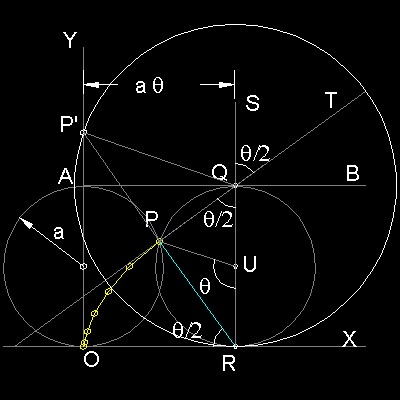
Point P on a circle with radius "a" is at point O initially. After this circle rolls along X-axis by θ, top, center and bottom of this circle are points Q,R & U respectively. Since R is the instantaneous center of rotation, ∠RPQ is a right angle, and line PT is tangent to the curve formed by locus of P. Additionally, it is shown that ∠PUR = θ, and ∠PRO = ∠PQR = ∠SQT = θ/2 Length of OR = a θ. This yields the following parametric equation for cycloid. x = a(θ - sin θ) y = 2a(1 - cosθ) Envelope of many lines like "PT" , will make a cycloid as shown above. This can be accomplished by either of the two ways: (1)Draw a horizontal line AB with lenght 2π, and divide in n equal lengths. Draw a line at each point with an angle incremented by 2π/n. (2)Draw a circle with radius 2a, and draw a diameter vertical initially at O. Roll this big circle along X a-xis, then the envelope of this diameter forms cycloid. The reason is that when the big circle comes to R, ∠RQP' = θ and PT is a part of the diameter.
*************** cycloid_model.dwg ***************
To create this drawing :
Load cycloid1.lsp (load "cycloid1")
Then from command line, type draw_cycloid_model
Use 20 division and stop execution at the 7-th step. Modify the drawing .
2.2 Epi-cycloid
The Epicycloid is generated by a point of a circle rolling externally upon a fixed circle.Examples of Epicycloid
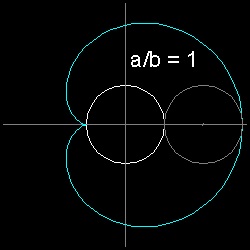
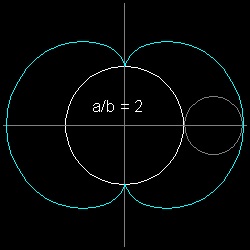
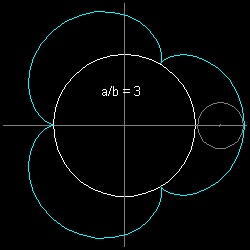
** epicycloid_cardioid.dwg
** epicycloid_nephroid.dwg
** epicycloid_cremona.dwg
** draw cardioid-animation
** draw nephroid-animation
** draw cremona-animation
Description of Epicycloid
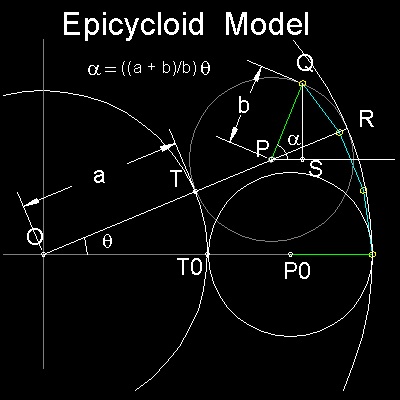
T.B.A.
************* epicycloid_model.dwg *************
To create this drawing :
Load cycloid1.lsp (load "cycloid1")
Then from command line, type draw_cycloid_model
Use 20 division and stop execution at the 7-th step. Modify the drawing .
Epicycloid by String Art (Curve Stitching)

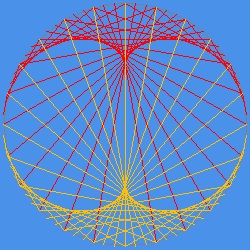
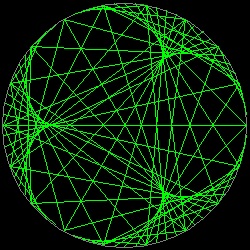
**** string_cardioid.dwg****
**** string_nephroid.dwg****
**** string_cremona.dwg****
** draw cardioid-animation
** draw nephroid-animation
** draw cremona-animation
2.3 Hypo-cycloid
Under constructionReferences
- Yates, Robert C.: A Handbook on Curves and their Properties. J.W.Edwards,1947.
- Lockwood,E.H.: A Book of Curves. Cambridge University Press, First edition published in 1961 .
- Millington, Jon: Curve Stitching. Tarquin Publications.1989.
- Downs, J.D.: Practical Conic Sections.-The geometric properties of ellipses,parabolas and hyperbolas. Dovers. First edition published in 1931.
- Kendig,Keith: Conics, Mathematical Association of America, 2005.
- Salmon, George: A Treatise on Conic Sections. Chelsea Publishing Company. Reprint. Original published in 1900.
- Hilbert,D.,Cohen-Vossen S.: Geometry and Imagination. Chelsea Publishing Company, English Translation. Original was published in 1932.