How to catch up a boat.--Apollonius circle
List of animations posted on this page.(Click the text to watch animation.)Case (a) Facing each other
Case (b) Chasing behind on a line
Case (c) General case
Suppose a ship leaves point B and steams in a fixed direction at a constant speed. A second ship,leaving point A at the same time, can go K times as fast as the first ship. Assuming a plane ocean,what course should the first ship steer in order to intercept the slow ship as quickly as possible ?
******* Apollo_circle_00.dwg ********
Let us begin with two very simple hypothetical cases when both ships are on the same line.
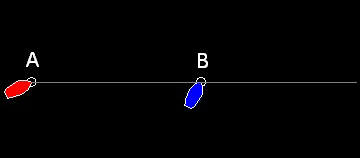
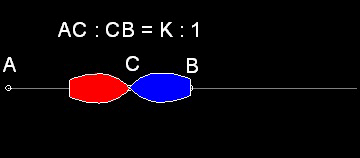
Case (a) Facing each other
It is easy to guess that two ships will meet at Point C,
which divides line AB internally to the K:1 ratio,i.e AC:CB = K : 1
******* Apollo_circle_01.dwg ******** ******* Apollo_circle_01A.dwg *******
You can see the process in animation.
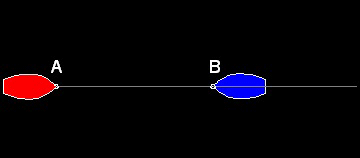
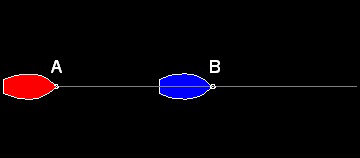
Case (b) Chasing on the same straight line
In this case the Chaser will catch up the slower ship at Point D,
which divides line AB externally to the K:1 ratio,i.e AD:BD = K:1
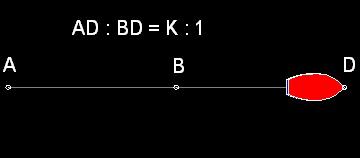
******* Apollo_circle_02.dwg ********
******** Apollo_circle_02A.dwg ********
You can see the process in animation.
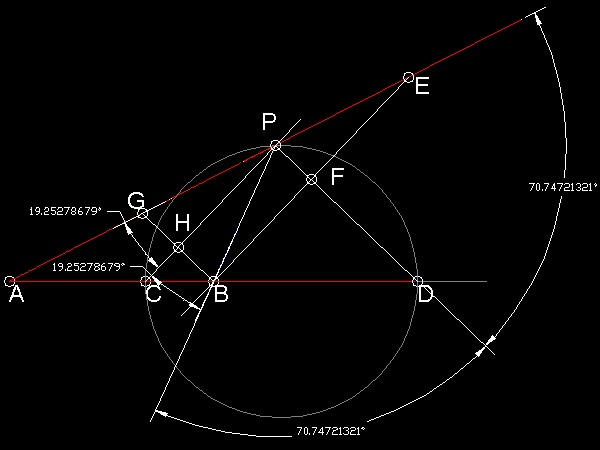
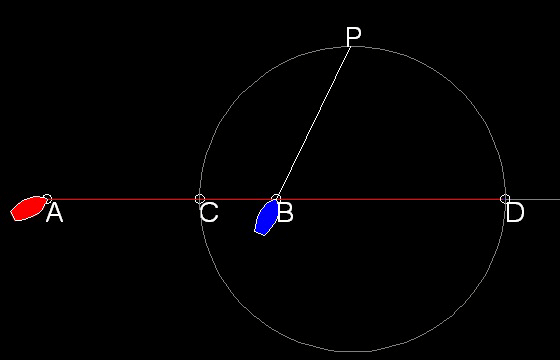
Case (c) More general case
What direction the boat "A" should take when the slower boat is moving in the direction
not colinear with line AB as shown below ?

******* Apollo_circle_00.dwg ********
Suppose the point of interception is P. Then this point P has to satisfy the following condition:
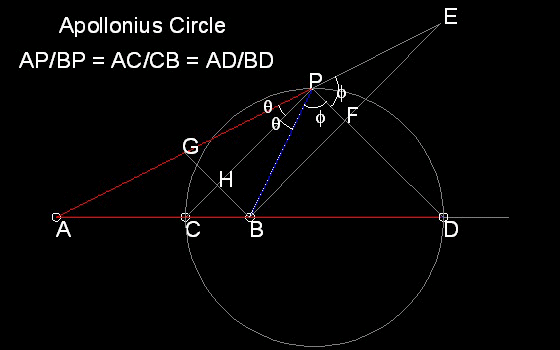
AP:BP = K : 1For example let the value of K be set equal to 2. Draw a circle with its center at B and radius R1. Then draw a circle with its center at A and radius K times R1. Locate the intersection points. Do this process a few times. The result is as follows:
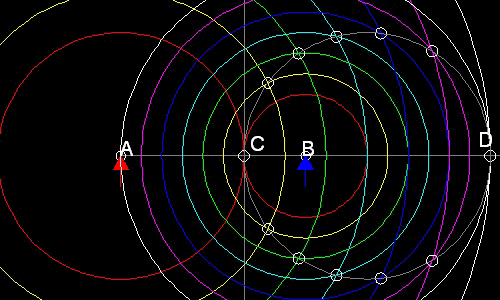
You will notice the following:
1. Points C & D are the cases when a pair of circles are tangent.(red and white circles.)
2. All the intersection points are on the circle with CD as a diameter.(yellow,cyan,blue,& magenta circles)
To draw multiple Apollonius circles
Load pursuit_Apollonius.lsp (load "pursuit_Apollonius")
from command line, type test_circle
red_arrow.dwg & blue_arrow.dwg are required.
******************* Apollo_03.dwg **********************
The Geeek mathematician Apollonius discovered that a circle may be defined in a way quite
different from the usual "all points equidistant from a fixed point."
Apollonius's defintion states that if a point moves in such a way that its distance from
one fixed point is always a constant multiple of its distance from another fixed point,
then its path is a circle.
- Based on the value of K, find out the position C & D.
- Draw a circle with CD as a diameter.
- Find out the point P on the circle where the slower ship is heading for.
- Steer the boat to the direction of Point P.
You can see the process in animation.
To create this drawing and animation:
Load pursuit_Apollonius.lsp (load "pursuit_Apollonius")
To see case (a),(b),& (c)
from command line, type pursuit_test
Case (a), (b) & (c) runs continuously.
Note* : This program requires red_boat.dwg & blue_boat.dwg .
********************** Apollo_1c_0.dwg ************************