Dogs at corners of a triangle chasing each other's tail.--Brocard point ,Equiangular spiral
List of animations posted on this page.(Click the text to watch animation.)Brocard Point Definition
3 dogs chase - Clockwise
3 dogs chase -Counter clockwise
If the triangle is equilateral, all three dogs will converge to the center of the triangle at the same speed.
But in case the triangle is not equilateral,is it still possible to get all the dogs at one point ?
And the answer is YES !
Recall from the previous section that the requirement for three dogs converging at one point is
the triangle connecting 3 dogs will remain similar to the original triangle.
One way to accomplish this is shown in the following drawing.
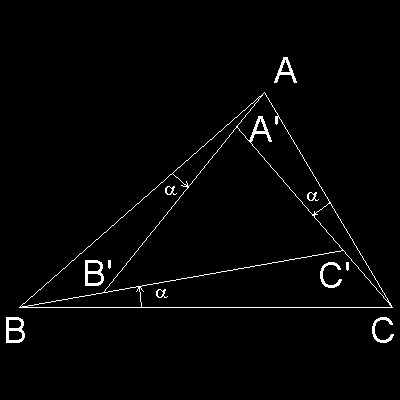
It is easy to show that Ð ABC = Ð A'B'C', Ð BCA = Ð B'C'A',etc.
Therefore as the angle a increase its value from zero to the direction specified in the drawing,
the triangle A'B'C' will always remain similar to the original triangle ABC.
What happens if the angle a is increased from zero to 180. degrees, and triangle A'B'C' is drawn
on the way ?
The resulting picture is shown in the next drawing, and the process is shown in animation.
*********** Brocard_pnt_1.dwg ************
************ Brocard_defa.dwg *************
******** Brocard_defa_zoom.dwg *********
To create this drawing and animation file.:
Load brocard.lsp (load "brocard")
from command line, type brocard_defa
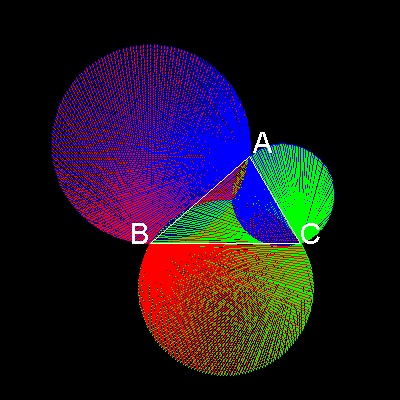
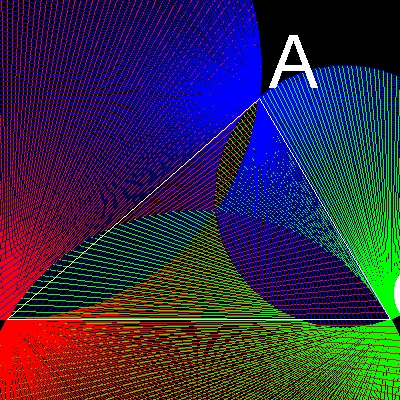
We can easily notice 2 important facts.
(1) There exists a point where the triangle converges to zero area somewhere near the center of the triangle.
(2) This point is also the intersection of 3 circles,
the first circle passing through point A and tangent to the line segment BC at point B,
the second one passing through point B and tangent to the line segment CA at point C,
the third one passing through point C and tangent to the line segment CA at point A.
**Note here that second finding from the zoomed picture is amazing because it is one graphical way to define such a point.
The point where the dogs converge is called "Brocard" point named after
Henri Brocard(1845-1922), a French army officer, who
described them in 1875.However, they had been studied earlier by
Carl Jacobi(1804-1851), and also by
August Crelle(1780-1855), in 1816.
But the works of these latter two persons have been forgotten until Brocard reinvigourated the interest of mathematicians.
During the period of about half a century beginning about the year 1875 ,"Euclidean Geometry" received revived attentions from
many mathematicians, and many marvelous results were published in papers.Brocard point was one of the popular topics then.(Ref 8)
Now we know there are many ways to find the location. Once the location is found, the 3 dogs chase can be
started by setting the speed of each dog proportional to the distance between this point and each dog's initial position.
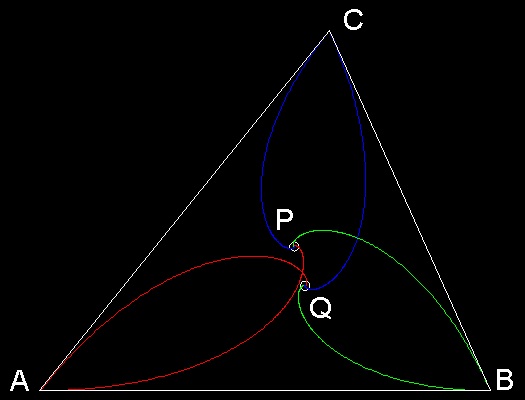
There are 2 "Brocard Point" in general. Each of them is the destination of 3 dogs-chase, clockwise and counter clockwise chase.
Here,the result of both cases are shown in one figure.
Counter Clockwise chase(Point A -> B -> C) ends at Point "P", and
Clockwise chase (Point A -> C -> B) , at Point "Q".
Only the Clockwise chase is shown in animation.
To create this drawing :
Load brocard.lsp (load "brocard")
For clockwise chase (Q)
from command line, type brocard2_cw
when the excution is done, type (single_win)
Then zoom with "Extent" option
For counter-clockwise chase (P)
from command line, type brocard2_ccw
when the excution is done, type (single_win)
Then zoom with "Extent" option
Note:The length of unit-step(=speed) each dog takes is proportinal to the initial distance from point A,B & C to Brocard point(P & Q).
Note* : This program requires prec_bar.dwg
and prec_meter.dwg
****************** Brocard_pnt_1.dwg *******************
How to find out the "Brocard Point"
For any triangle there is a unique angle theta,the Brocard angle,such that the lines in the figure
concur,at the Brocard points P and Q.
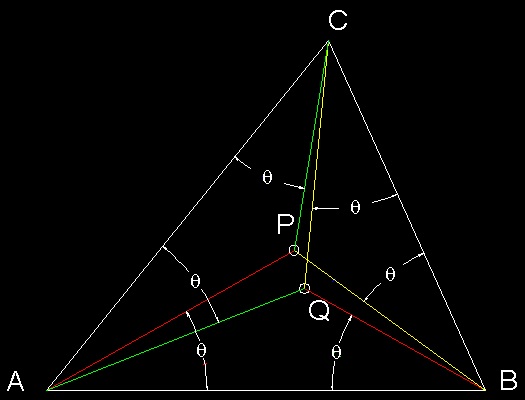 As shown in the previous section, the arc length of the pursuit curve(equiangular spiral) is proportional to the distance from each
vertex to the center (point P & Q).
As shown in the previous section, the arc length of the pursuit curve(equiangular spiral) is proportional to the distance from each
vertex to the center (point P & Q).
For example in counter clockwise chase case, the arc length a dog initally at point A has to travel
by the time it overtakes a dog intitally at point B is AP/cos(q).
If the speed of the 3 dogs at points A,B & C are set proportional to the distance AP, BP & CP,then
these 3 dogs will meet at point P. The same argument applies to the point Q in clockwise chase case.
****************** Brocard_pnt_2.dwg *******************
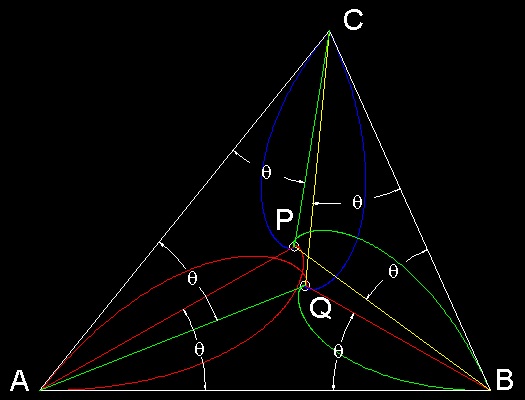
The equilateral triangle case shown in the previous section is a special case when P & Q are at the same location.
But in general triangle case, there exist 2 Brocard points corresponding to cw and ccw chase case.
******************* Brocard_pnt_3.dwg ********************
Analytical definition of Brocard point:
The Brocard angle is given by this formula whose simplicity suggests that it must be significant: cot q = cot A + cot B + cot C where angles A, B, & C are angles at the points A,B & C respectively.Geometrical definition of Brocard point:
The Brocard points can be constructed geometrically by drawing the circles that pass through two vertices,touching one side, as in this next figure. The circles touching line AB at A, and passing through point C,and so on ,define one Brocard point (Brocard_ccw_geom.dwg),and the circles touching line AB at B,passing through point C and so on,would define the other. (Brocard_cw_geom.dwg)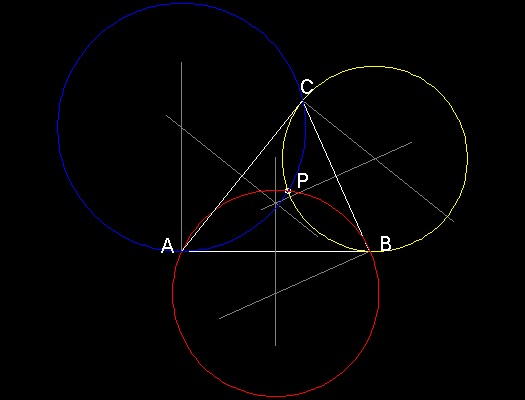
**************** Brocard_ccw_geom.dwg ****************
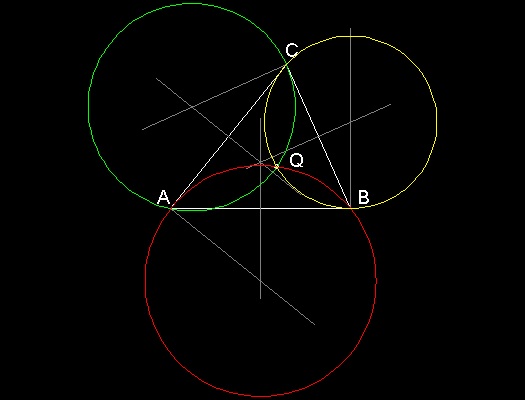
**************** Brocard_cw_geom.dwg *****************
More on Brocard point
In order to find the Brocard point geometrically(i.e.as a point three circles concur), it is easier
to use function copy_rotate to find out the center of these circles.
For a normal bisection of the line conecting point A & B, select the line ab, and select mid point as
a center of rotation, and rotate 90 degrees(in this case plus or minus does not matter).
To draw a line normal to line AC at point A, issue this command copy_rotate , select line AC, rotate the line around point A by -90 degrees(clock wise is minus !). The intersectin of these 2 lines is the center of one circle used in defining Brocard point.
Another way to find the Brocard point is as explained in Ref.8.
The steps are:
Draw a circle (Z) passing through B , and tangent to line CA at point C.
If the line through C parallel to AB meets Z at D, then DA intersects Z at the Brocard point P.
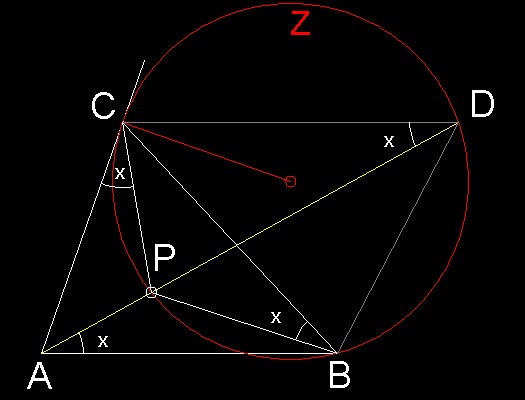
****************** Brocard_angle_0.dwg ******************
Each of the pertinent angle at A,B,and C is simply the angle x = ÐCDP:
- Ð PCA because CA is an tangent and CP a chord;
- Ð PAB because CD // AB; and
- Ð PBC is in the same segment of Z as Ð CDP
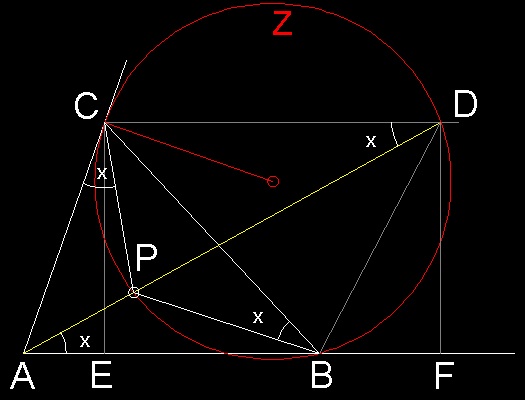
****************** Brocard_angle_1.dwg *****************
Now,let DF be drawn perpendicular to AB and let CE be the altitude from C.
Then CEFD is a rectangle and CE = DF. Because CA is a tangent to Z, we have
ÐC = ÐACB = ÐCDB, and with the parallel lines,
the equal alternate angles at D and B give Ð DBF = Ð C.
Since Ð DAF = x, we have
cot(x) = AF/DF = (AE + EB + BF)/DF = AE/CE + EB/CE + BF/DF (recall DF = CE)
= cot A + cot B + cot C
which will give the Brocard angle value.
Sample results for a general triangle case
-Counter ClockWise Chase-
You can see the process in animation.
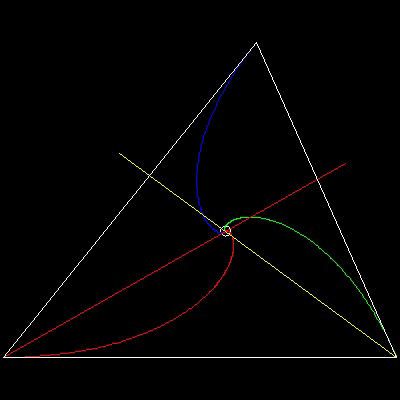
To create this drawing and animation:
Load brocard.lsp (load "brocard")
from command line, type brocard2_ccw
(setup_tri_ccw) will set up triangle ABC with Brocard point.
(c:omega) will compute the Brocard angle "omega" using trigonometric equation
cot q = cot A + cot B + cot C
********** 3dogs_ccw_result.dwg *********
-ClockWise Chase-
You can see the process in animation.
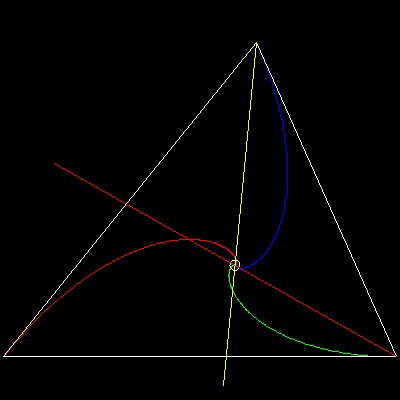 To create this drawing and animation:
To create this drawing and animation:
Load brocard.lsp (load "brocard")
from command line, type brocard2_cw
(setup_tri_cw) will set up triangle ABC with Brocard point.
(c:omega) will compute the Brocard angle "omega" using trigonometric equation
cot q = cot A + cot B + cot C
********** 3dogs_cw_result.dwg **********
Try to see the following by yourself.
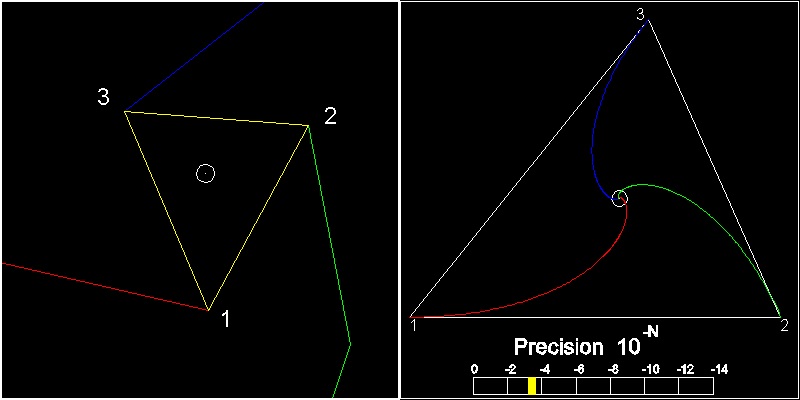
When the program stops, we see 2 windows, total view, and the zoomed-up center area.
3 end points are connected to form a triangle. The direction of naming the apexes is according to the
base triangle. So end of red is "1", end of green is "2",and the remaining one is 3.
If this yellow triangle's point 2 & 3 are aligned to the points 2 & 3 of the base triangle, you will find out that both triangles are similar,(same angles ,only the scale difference!!)
This is what we have seen in the case of 4-dogs at the square court: positions of 4 dogs always
form a square all through the chasing period.
************************************* ccw_result_1.dwg *************************************