Generalized Linear Pursuit Case
Alfred J.Lotka in Ref.1 looked at the pursuit problem from a different angle, and his result can be appliedto a general linear pursuit problem.
Background of the discussion
An organism P1 , of a species which serves as food to an organism P2 , becomes aware of the presence of the latterwhen at a distance r from the same, and immediately flees in a straight line to the nearest cover or refuge, distance D away.
What is the criteria of the capture or escape of the organims P1 ?
This is a standard linear pursuit problem, and nothing special about it.
The pairs of the pursuer and the pursued can be dog and rabbit,
spider and fly, peacock and snake, etc.
But Ref.1 posed the question in a slightly different manner.
Condition:
Let P1 be the point pursued, which moves with a constant velocity v1
Question:
and in a striaght line P1O.
Let P2 be the pursuing point,which moves always in the direction P2P1,
with a constant velocity v2.
If v2> v1, P2 will ultimately catch up with P1 at some fixed point O.
O is the point of capture.
******* ellipse_derivation_1.dwg ********
For a given ratio v2 / v1= e, and a given direction of v1,
what is locus of all those positions at time t of the pursuing point,
which will result in capture at the given point O ?
The following derivation is credited to Professor F.R.Sharpe.
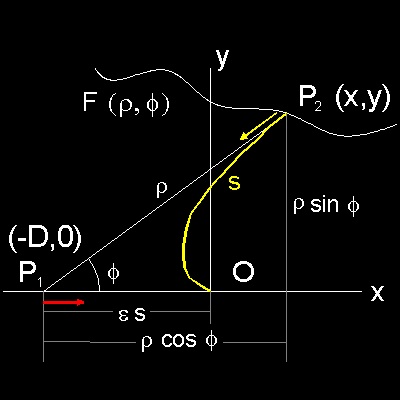
x = -es + rcos(f) y = rsin(f)
where f is the angle P2 P1O, and r is the radius vector P1 P2.
Differentiating we have:
(dx/ds) = -e + (dr/ds)cosf - rsinf (dr/ds) = -cosf
(dy/ds) = (dr/ds)sinf + rcosf(dr/ds) = sinf
Solving we have
(dr/ds) = 1 + ecosf
r(dr/ds) = e sinf
Hence
(1- ecosf)(dr/ds) + e r sinf(df/ds) = 1 - e2 Integrating, (1- ecosf) r = (1 - e2)s This is an equation for an ellipse with eccentricity e,
and s is the length of semi-major axis(usually called "a").
D is the distance of the foci from the center and D = e a
Answer to the general linear pursuit problem
We can use this result to answer a more general linear pursuit problem.
General problem:
A prey is sitting at point "F" (-c, 0) and there is a absolutely safe haven at point "O" (0,0).
The speed of the prey in escape is v1.
The prey found a predator at "P" (x,y) , and the predator runs at the constant speed of v2.
The prey and predator starts running at the same instance, prey toward point "O", and predator
toward the direction of the prey.
What is the criteria of escape or capture assuming v2 > v1 ?
Answer:
If the point P is outside this ellipse,
the capture will not happen.
Draw an ellipse with semi-major axis a= (v2/v1)c, with point F as one of the foci.
How ?
1. graphically: draw a circle with center at F, and radius a. This will intersect positive y-axis at B.
OB = b (semi minor axis) Draw an ellipse using a and b values.
2. Compute b value by b = a (1 - e2)1/2, where e = v1/v2
Example runs
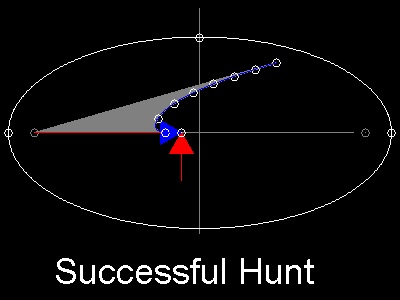If the dog is within the ellipse, then the dog can catch
the rabbit before the rabbit reaches the safe hole.
********** successful_hunt.dwg ***********
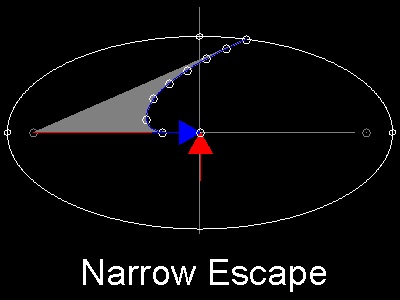If the dog starts from a point on the ellipse, then the rabbit reaches
the safe hole when the dog is at the rabbit's heel. Narrow escape !!
********** narrow_escape.dwg ***********
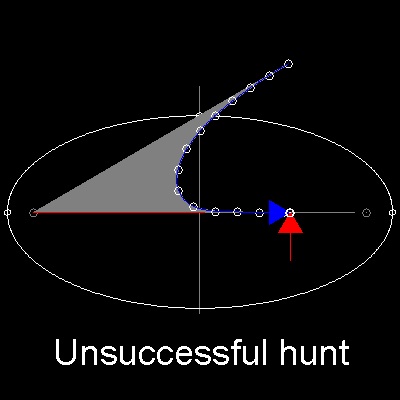If the dog begins his chase from a point outside the ellipse,
then the dog cannot catch the rabbit before rabbit reaches the safe hole.
********** unsuccessful_hunt.dwg ***********