How to draw a heart shaped figure (if possible with compass and ruler)
It all began with Loyd's "Red Heart" Dissection puzzle.|
click here to enlarge "Red Heart Quiz"  |
click here to enlarge Answer to the Puzzle  |
Several years ago,the author came across Sam Loyd's "Red Spade Quiz". According to [Ref. 1,2,3],
Sam Loyd , during his visit to Crescent City (near New Orleans ?) saw a stained glass decoration depicting a "red spade" (shown above), although the insignia of the club house was supposed to be "the ace of hearts".
Upon further inspection he found out that this "red spade" was composed of three pieces. He then figured out that by proper arrangement of the three pieces, they would be fitted together so as to form the "ace of hearts", as originally desired. He then proposed the following quiz.
Answer to the quiz is given in the same referenced books.
The first thing the author has to find out is what are really the shapes of "heart" and "spade".
The readers will be really surprised to see that there are so much informations regarding the heart shape in many languages. The most of the contents of this web site are based on the informations contained in the follwoing web sites. The other sites are also listed at the end of this article.
Regarding the Heart Shapes and Spiral Curves:
The following four web sites are very comprehensive and a fun to read.
In English
(Original was written in German (see below). Translated into English)
Wikipedia Heart(symbol)
In German
In French
My web search has been less successful regarding the shape of "spade".
So I have decided to reverse the direction of the propostion, and tried to dissect
an heart shaped figure into "spade" look-like figure.
Preliminary studies:
Wikipedia Heart_(symbol)
lists 3 heart shapes which can be expressed in ,
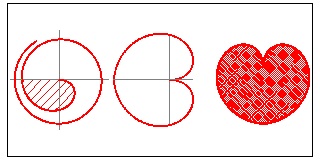
(1) analytical form :Classical "cardioid",
(2) implicit form in Cartesian coordinate(x,y),
(3) parametric form in polar coordinate.
Three results are shown below.
I also colored Heart and Spade according to the commonly accepted way.
See how the color changes from red to black counter clockwise as "Heart"
is transformed into "Spade"..
1. Solution by the well-known analytical "heart" curves
click here to enlarge
Cardioid :
defined in polar coordinate as : R = a*(cost + 1)
***** Download this drawing(DWG format) ***
click here to enlarge

Parametric form in polar coordinate :
x = 16 sin3t
y = 13 cost - 5 cos2t - 2cos3t - cos4t
***** Download this drawing(DWG format) ***
click here to enlarge
 Implicit form in Cartesian coordinate :
Implicit form in Cartesian coordinate :f(x,y) = (x2 + y2 - 1)3 - x2y3 = 0
Note to the readers who want to draw this figure:
Using the polar coordinate, this curve can be rewritten as
f(r,t) = (r2 - 1)3 - r5(cost)2(sint)3 = 0
C Then for a given angle t, search the root for r using Newton iteration.
***** Download this drawing(DWG format) ***
It is clear that none of the above give a beautiful set of heart and spade.
The biggest problem is that the resulting spade has a sharp spiked tip.
To avoid this , the starting heart shape must has a rather flat bottom
like cardioid. But cardioid does not have a sharp mound on the top, so it is hard
to be called a heart shape.
This motivates the author to explore other methods of drawing "heart shape".
The final goal of this effort is to find out how to draw a heart shape which can be used
as a solution to Sam Loyd's "Red Spade Quiz".
2. Heart-Shaped things around us
It is surprising that heart-shape can be found everywhere around us, in your garden, shopping mall, on the road side, and inside our home. The author took these digital pictures and imported to the AutoCAD, and normalized the height of the heart so that shape comparison makes sense.Each frame below is set to be square with 1.2 unit, and the vertical length of the heart shape is set to 1.0 so that it is easier to compare the shape difference.
Here is a simple description of these images. Characters in the pictures are erased.
(1)~(5), (9), (10) Plant leaves around the house
(6),(7) Heart-shaped Jewelries
(8) Heart-shaped picture frame
(11) A walnut shell found on the roadside
(12) A chair in the sunroom
(13) A garden door iron-work
(14) A heart-shaped soap
(15) A floor sign in the store
(16) A merchandise in a gift shop
(17) Traditional European heart shape shown in Wikipedia
(18) Heart ace symbol used in a playing card(enlarged)
(19)~(21) Heart shapes used in Newspaper Ad.
(22),(23),(25) Signs on the store front glasses
(24) A box of chocolate
(26),(27),(28) Heart design on the shopping bags
What is the characteristic of "heart like shape" ?
Examples of typical heart shapes are drawn using only curves everyone is familiar with,namely stright line, circle , ellipse and sine curve.
Top region : a groove in the center, and symmetric arcs on both sides
Lower region : There seems to be 4 different patterns.
1. straight line Ex. (1) below
2. arc protruding outside all the way to the bottom
(curvature sign does not change) Ex. (2-a) ,(3) below
3. arc's curvature's sign changes as it goes down. Ex. (2-b) below
4. tangent at the bottom is horizontal.(center of the arc is on the vertical axis) Ex. (4) below
| click here to enlarge (1) Circle & Line 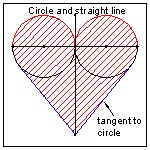 |
click here to enlarge (2-a) Circle & Sine #1  |
click here to enlarge (2-b) Circle & Sine #2 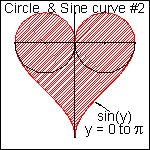 |
click here to enlarge (3-q) Heart from Ellipses  |
| click here to enlarge (3-b) Heart from Ellipses  |
click here to enlarge (4) Three Arcs Heart 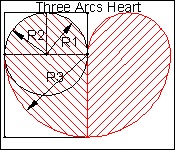 |
"(1) Circle & Line" Heart
Let us take a closer look at "(1) Circle & Line " Heart shape.
This reminds the author of "One Cut Origami" by
Except the case of "Diamond", it is not a trivial task to create the other 3 shapes from a square paper and one time straight scissor cut.
| click here to enlarge One Cut Heart  |
click here to enlarge One Cut Spades  |
click here to enlarge One Cut Clover  |
click here to enlarge One Cut Diamond  |
The next picture illustrates how a piece of paper napkin changes into a "heart-shaped" figure.
click here to enlarge

After making the origami heart, the author has studied the crease lines and found out that "One cut Heart"
is a special case of the more general method of heart shape construction.
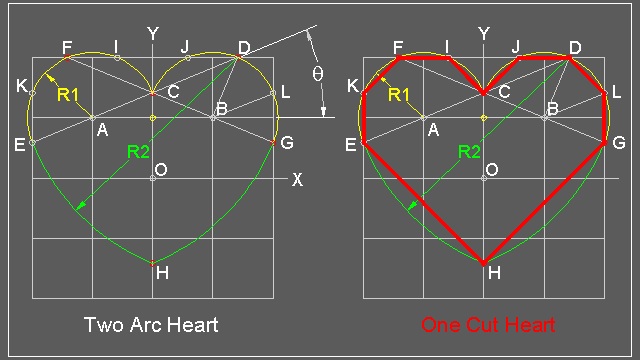
In the picture shown below, the Scissor cut line is shown in bold red lines. In the actual operation , it is just one straight scissor cut (surprised ?)
The whole process can be summarized as follows:
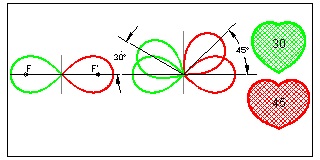
1. draw grid lines with one unit spacing. Identify x & y axis.
2. draw a line from point A with angle theta from X-axis intersecting Y-axis at point "C".
Range of angle theta is from 0 to 45 degrees,
Note: One Cut Heart is a special case of theta = 22.5 degrees.
3. Draw a semi-circle with its center at "A" and radiius AC. Do a silmilar opration for point "B"
4. The intersection of AC extension and a circle with its center at "B" is "D"
5. Begin drawing arc from "C" ,then "F" and "E".
6. When this arc reaches "E" , the center of arc moves from "A" to "D" and continue the arcing process
using Radius R2 until it touches Y-axis("H")
The process (5 ,6) is shown in animation. Click here to see Simple Heart Creation animation
************************ Download this drawing(DWG format) **********************
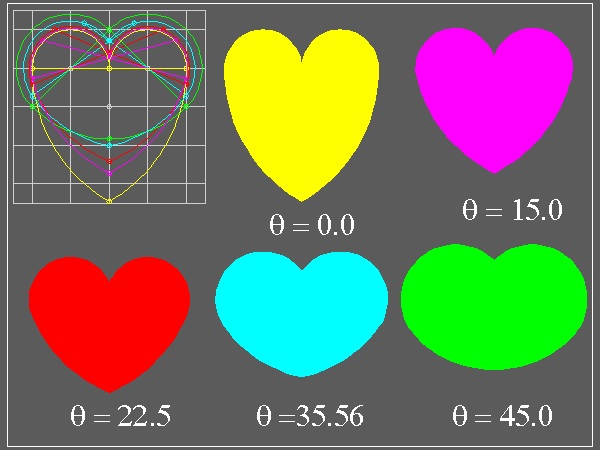
Changing parameter angle from 0 to 45, it is easy to create a series of heart shapes
made up of two arcs. The result are shown below.
θ = 22.5 ° case corresponds to "One cut Origami" heart .
************************ Download this drawing(DWG format) **********************
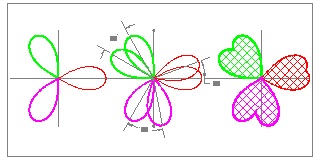
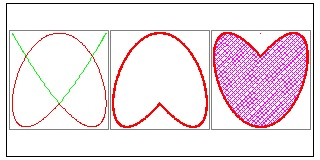
(3) Heart from Ellipses
It is well known that cutting an ellipse through the center line, and add a mirror image will create a heart shape . It is also patented by an American in 1980's !
Click here to see Ellipse to Heart animation.
In general two hearts are created by this operation..
Three examples are shown below.
************************ Download this drawing(DWG format) **********************
A general formula for an ellipse is given as follows:
(X/a)2 + (Y/b)2 = 1 (1)
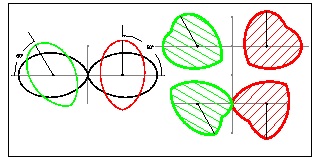
Application of counter clock wise rotation by angle "θ" is equivalent to applying the following transformation.
X = (cos θ)*x + (sin θ)*y , Y = - (sin θ)*x + (cos θ)* y
The result is:
(b2cos2 θ + a2sin2 θ) x2 - 2(a2 -b2)(sin θ)(cos θ) xy + (b2sin2 θ + a2cos2 θ) y2 - a2b2 = 0 (2)
The generality of this expression is not lost by assuming ab = 1. This leads to
(b2cos2 θ + a2sin2 θ) x2 - 2(a2 -b2)(sin θ)(cos θ) xy + (b2sin2 θ + a2cos2 θ) y2 - 1 = 0 (3)
Applying the scaling coordinate transformation such that ξ = λ*x and η= μ*y
where λ2 = (b2cos2 θ + a2sin2 θ) and μ2 = (b2sin2 θ + a2cos2 θ) ,
and using the relation λ2*μ2 - (a2-b2)2 sin2θcos2θ = a2b2 = 1
(3) can be written as
{ η - (a2-b2)(sin θ)(cos θ)ξ/λμ }2 + (ξ/λμ)2 - 1 = 0 (4)
Introducing scaling trnsformation once again for ξ such that ζ = ξ/λμ and moving all terms except η
to the right hand side, the final formula looks like this in terms of η and ζ.
η = (a2-b2)(sin θ)(cos θ)ζ ± √(1 - ζ2 ) (5)
Note:Instead of ξ = λ*x, ξ = x / μ could have been used.
Then ζ in (5) could been replaced by ξ and it was not necessary to use
one more coordinate variable ζ.; But at the
early stage of this algebraic exercise, it was not that obvious to the author.
A very special case: a nd b are chosen to be "golden ratio".
When a = (1 + √5)/2 (≅1.61803...) and b = (√5 - 1)/2 (≅0.61803..) (Golden ratio !!),
and rotation angle θ satifies
the condition sin(2θ) = 2/√5 ; cos(2θ) = -1/√5
eqution (5) can be written in a very simple form:
y = x ± √(1 - x2)
(6)
Or in a fully expanded form:
2x2 - 2xy + y2 - 1 = 0
(7-a)
Mirror image of this function is given by;
2x2 + 2xy + y2 - 1 = 0
(7-b)
This transformation is illustrated graphically in the drawing below.
click here to enlarge
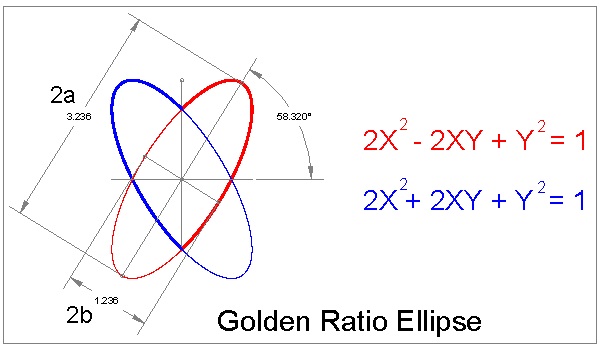
Interpretation of equation (6)
click here to enlarge
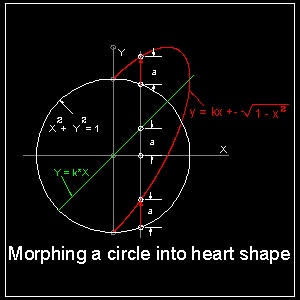
Nobuo Yamamoto,
realized that by changing x to kx
with parameter k changing from 0 to 1, he could obtain a series of heart shapes.
The idea was described in the picture shown here.
The first term is a line passing through the coordinate origin with
its slope k being 1.
The second term is a unit radius circle with its center at the origin.
In the range x≥0, both the lower and upper halves of the circle are lifted by the amount of "kx" as x increase its value to the right until it reaches the final value 1.0.
This process is shown in animation.
Click here to see Circle To Heart animation
**** Download this drawing(DWG format) ****
See also Norbert Herrmann's book (Ref. 10) for discussion on eq.(6).
Readers may have noticed by now that this incremental function kx can be replaced by
other simple
polynomial function of X such as |X|p and p will be 1/2, 2/3,...
Nobuo Yamamoto,
dealt with k*|x|1/2 case,changing k from 0 to 1,and showed many heart shapes..
Actually there are a few different ways to present a general formula.
Here are typical examples:
Y = α*|X|p ± √( q - X2 )
(8-a)
where p,q and α are constant values.
Using (8-a) , four different heart shapes are created and compared.
For comparison purpose,the height of each drawing is normalized to a unit value.
Parameter values and names credited to are taken from
Jürgen Köller's Herzcurve
click here to enlarge
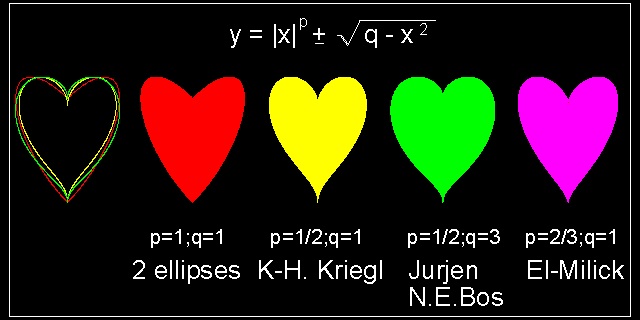
************************ Download this drawing(DWG format) **********************
By replacing a unit circle by an ellipse
2*y2 + x2 = 1
another general formula looks like this.
X2 + 2( Y - p|X|q )2 = 1
(8-b)
where p,q and α are constant values.
Using (8-b) , five different heart shapes are created and compared.
Here again, parameter values are taken from
Jürgen Köller's Herzcurve
click here to enlarge
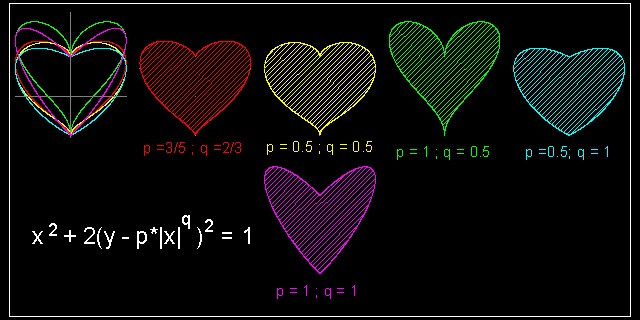
************************ Download this drawing(DWG format) **********************
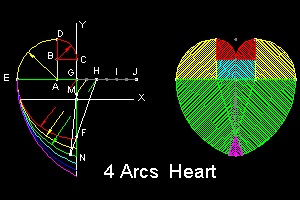
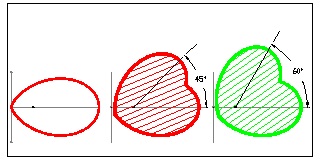
(4) Three Arcs Heart
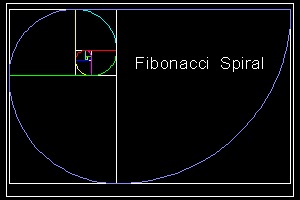
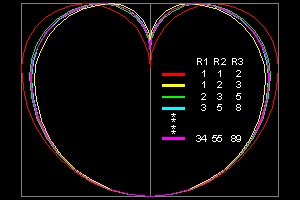
Though R1 = R2, R2 is added here because R1, R2, R3 is the first group of three Fibonacci number. It is well known that Fibonacci number sequence makes a spiral shape.
Refer to the first three pictures below.
click here to enlarge click here to enlarge
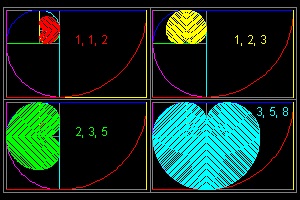
**** Download this drawing(DWG format) **** **** Download this drawing(DWG format) ****
click here to enlarge click here to enlarge
**** Download this drawing(DWG format) **** **** Download this drawing(DWG format) ****
Let us take a closer look at (1, 2, 3) arc case. (refer to the "4 Arcs heart" above)
This is how the heart shape is drawn.
First arc: radius = 1, arc starts from C with its center at B and ends at D.
Second arc: radius = 2, then arc center moves from B to A along the line DB and arc ends at E.
Third arc: radius = 3, the arc center moves from A to G along the line EA and ends at
Y-axis(axis of symmetry)
This means that center of radius is allowed to move only on the line connecting the end of the arc and its center of radius..This guarantees the smooth continuity of tangent line where the radius changes its value.
Then as far as the third arc is concerned, it is possible to choose any points on the line connecting E to G,, and extending further out to J.
Suppose such a point H (EH = 4) is chosen. It will make an arc
And green arc ends at Y-axis. Pick a point N on the arc just left of Y-axis.
The line connecting HN cuts Y-axis at F.
Now use this point F, and radius FN as a new set of arc at the bottom of the heart form.
It is permissible because change of arc's center occurs on the line HN.
The result is shown in the picture above.
The above process guarantees a rather flat stake at the top when this heart is used to change into spade configuration.
Using this idea, a new heart shape is changed into spade shape.
Heart to Spade dissection using 4 arcs heart shape
click here to enlarge

********** Download this drawing(DWG format) **********
There are many heart shapes which can be drawn using analytical curves.
More analytical Hearts
In general any analytical curves which have spiral-like feature can be used to construct heart-like shapes.
It is also possible (like a case in ellipse) to construct a heart-like fugure from many closed curves,
for example, lemniscate, folium, Cassinian oval,etc.
(1) Logarithmin,integral,polynomial,involute type spirals group
First, there are several spirals which are written in the form: Rm = amθ2. They are
1. Archimedes' spiral (m = 1; n = 1)
2. Fermat's spiral (m = 2; n = 1)
3. hyperbolic spiral (m = 1; n = -1)
4. Galileo's spiral (m = 1; n = 2)
5. littus (m = 2; n = -1)
6. variation of Galileo's spiral ( R = θ2/(θ2 - 1) )
7. variation of hyperbolic ( R = θ/(θ - 1) )
Then there are more of integral, exponential and involute type.
8. Circle Involute
9. Cornu's spiral-Clothoid
10. The logarithnic (or equiangular) spiral
click here to enlarge
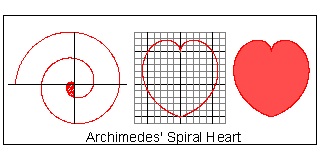
Archimedes' Spiral
In polar coordinate system, it can be written as:
R = K*θ
where K is contant and θ is an angle in radian.
**** Download this drawing(DWG format) ****
click here to enlarge
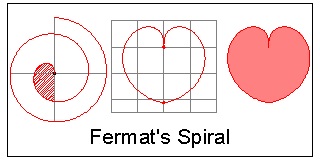
Fermat's Spiral
In polar coordinate system, it can be written as:
R = K*√θ
where K is contant and θ is an angle in radian.
This curve is also called "parabolic" because of
its analogy to y2 = a2*x
**** Download this drawing(DWG format) ****
click here to enlarge
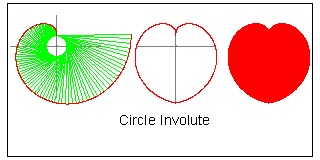
Circle Involute Spiral
Involute is defined as "the path of a point of a string:
tautly unwound from the curve (here, a circle)."
In mathematical terms, it is expressed as
x = R0(cosθ + θ*sinθ)
, y = R0(sinθ - θ*cosθ)
or,
R2 = R02(1+ θ2)
**** Download this drawing(DWG format) ****
click here to enlarge
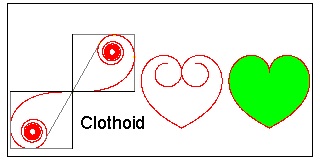
Clothoid (Cornu's Spiral)
The coordinte x,y are defined in Fresnel integral as:
x = ∫cos(π/2*u2)du
y = ∫sin(π/2*u2)du
where integration interval is from 0 to u.
In practice, integration can be replaced by the following summation.
x = ∑cos(π/2*ui2)*Δu
, y = ∑sin(π/2*ui2)*Δu
where u = n*Δu, and summation is from 1 to n.
**** Download this drawing(DWG format) ****
click here to enlarge
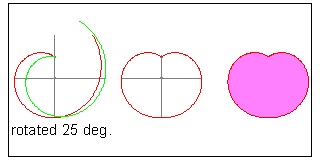
Equiangular Golden Spiral
In general equiangular(or logarithmic) spiral can be defied as:
R = Kθ
where K is contant and θ is an angle in radian.
In case K = (1+√5)/2 = 1.618... (golden ratio)
this curve is called "Golden Spiral".
**** Download this drawing(DWG format) ****
click here to enlarge
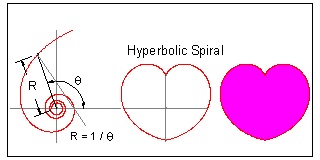
Hyperbolic Spiral
In polar coordinate system, it can be written as:
R = 1 / θ
where θ is an angle in radian.
The naming came from its analogy to the equation
xy = a
It is also called "Reciprocal" spiral.
**** Download this drawing(DWG format) ****
click here to enlarge
Galileo's Spiral
In polar coordinate system, it can be written as:
R = a + bθ2
In this drawing : a = -4, b = ±1
red line is for b=1, and green , for b=-1
The first 3 hearts are drawn with the same height.
**** Download this drawing(DWG format) ****
click here to enlarge
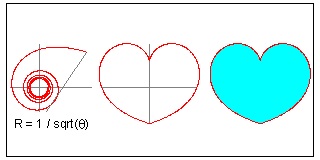
Lituus
The naming came from the shape of an acient
Roman trumpet.
In polar coordinate system, it can be written as:
R = 1 / √θ
where θ is an angle in radian.
**** Download this drawing(DWG format) ****
click here to enlarge

Snail #1
From Book ref 6.
In polar coordinate system, it can be written as:
R = θ2 / ( θ2 - 1 )
where θ is an angle in radian.
The curve is plotted for θ >= 1.2, and θ = 1 line is
an asymptote for θ = ± ∞:
**** Download this drawing(DWG format) ****
click here to enlarge
Snail #2
From Book ref 6.
In polar coordinate system, it can be written as:
R = θ / ( θ - 1 )
where θ is an angle in radian.
The curve is plotted for θ <= 0
**** Download this drawing(DWG format) ****
(2) Rm = cosnθ type (Lemniscate) group
1. Leminiscate of Bernoulli (m=n=2)
2. m=2, n=3 case
click here to enlarge
Bernoulli's lemniscate (m, n = 2 )
The product of distance from two poles is constant:
PF*PF' = d2
where F(0,-d),F'(0, d) are poles, P, a point on the
curve,and a =d√2, then the curve is written as:
Equation in (r,θ): R2 = a2cos2θ
Equation in (x, y): (x2+y2)2 = a2(x2-y2)
**** Download this drawing(DWG format) ****
click here to enlarge
m = 2, n = 3 case
No specific name is given to this curve.
Equation in (r,θ):
R2 = a2cos3θ
The results of rotation angles, 20°, 30°
and 40° are shown.
**** Download this drawing(DWG format) ****
(3) R = cosmθ type (Folium) group
1. Double Egg (m=2)
2. Simple Folium (Keplar's Egg) (m=3)
click here to enlarge
Double Egg (Münger-1894)
Equation in (r,θ): R = a*cos2θ
Equation in (x, y): (x2+y2)3 = a2*x4
Original curve was scaled by 1.2 in x_direction.
Angles of rotation are 60° and 90°, and their centers are (±0.6,0).
**** Download this drawing(DWG format) ****
click here to enlarge
Simple Folium (Kepler-1609 & Viviani-1647)
This curve is also called Kepler's Egg.
Equation in (r,θ):
R = a*cos3θ
Equation in (x, y):
(x2+y2)2 =
a*x3
**** Download this drawing(DWG format) ****
(4) Lissajou Curves(or Bowditch Curves)
In general it is written as
x = a*sin(nt + c)
y = b*sin(t)
During the late 19-th century in England, one of the popular parlour pastime was drawing mathematical arts using a device called "Harmonograph".(Ref. 11)
This device is made of either 2 or 3 pendulums. The simple model of 2 pendulums is designed such that one pendulum moves in x-direction, while the other, in y-direction when viewed from above. Result is that it draws some figure on the table top. To begin this operation, both penduluma are held at their limit range, then they are released at the same time to accomplish "in-phase" motion.
Click here to see drawing by pendulum motion .
A circle in the right is y-axis pendulum positin, and the bottom one , x-axis pendulum position.
Then the equation for the figure drawn on the table is given by:
x = a*sin(2πmt + π/2)
y = b*sin(2πnt + π/2)
where a & b represent the amplitude of the pendulum, and 2πm, 2πn are frequencies of two pendulums determined by the weight and pendulum length. Here we set these parameters such that m,n are both integers and a = b= 1 (unit value).
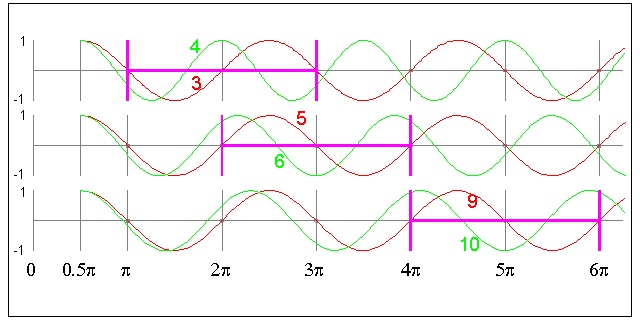
1. m = 3; n = 4 case
2. m = 5; n = 6 case
2. m = 9; n = 10 case
click here to enlarge
m = 3; n = 4 case
Equation in Cartesian coordinate system:
x = sin(6πt + π/2)
y = sin(8πt + π/2).
*where 1/12 ≤ t ≤ 5/12
Click here to see 3-4-heart creation animation
*refer to the note below
**** Download this drawing(DWG format) ****
click here to enlarge

m = 5; n = 6 case
Equation in Cartesian coordinate system:
x = sin(10πt + π/2)
y = sin(12πt + π/2)..
*where 3/20 ≤ t ≤ 7/20
Click here to see 5-6-heart creation animation
*refer to the note below
**** Download this drawing(DWG format) ****
More notes on "Harmonic-heart" by Harmonograph
click here to enlarge
********** Download this drawing(DWG format) **********
click here to enlarge

********** Download this drawing(DWG format) **********
8.3 Further examples of heart shape in analytical form
Heart-1x = 16 (sint)3
y = 13*cost - 5*cos2t - 2*cos3t - cos4t
draw right half (x >=0) for 0≤ t ≤π
Heart-2
Cartesian: (x2 + y2 -1)3 - x2*y3 = 0
Polar: (r2 - 1)3 - r5*(cost)2*(sint)3 = 0
Parameter from -π/2 to π/2 draws right half (x >=0) region.
Heart-7 method 5 in Heart Curve by Jürgen Köller
composite of (1/4) sine curve and semi-circle on the top
Heart-8 method 6 in Heart Curve by Jürgen Köller
composite of (1/2) sine curve and semi-circle on the top
Heart-9 From Wolfram's MathWorld (Feb 2010)--anonymous source
R = 2 -2*sin(t) +sin(t)*sqrt(|cos(t)|)/ (sin(t) + 7/5)
0≤ t ≤2π
Heart-10 Raphael Laporte (1993)
x = (sin theta)3
y = (cos theta) - (cos theta)4
Heart-11 Dwight Boddorf
r = (1 / tan(theta))(1/ tan(theta))
0 < theta < (1/2)* π note: no equality sign
Heart-12 Heart Curve by Hans-Jürgen #1
x = (-3t2 + 2t + 1) * sin(t)
y = (-3t2 + 2t + 1) * cos(t)
Heart-12A Heart Curve by Hans-Jürgen Casper #3
x = a(-t2 + 40t + 1200) * sin(π*t/180)
y = a(-t2 + 40t + 1200) * cos(π*t/180)
where t ranges from 0 to 60 degrees
for example a = 1/100 ;
Heart-13 Heart Curve by Hans-Jürgen #2
y = (2/3)*[(x2+|x|-6)/(x2+|x|+2) +- sqrt(36-x2)]
0<= x <= 6
Heart-14 similar to method 4 in Heart Curve by Jürgen Köller
in algebraic equation form
2X2 - 2XY + y2 - 1 = 0 (x>=0)
2X2 + 2XY + y2 - 1 = 0 (x<=0)
This is a very special case of ellipse (x/2)2 + (y/b)2 = 1
where a = (1 + (sqrt 5))/2, and b = ((sqrt 5) - 1)/2
Note: This is the golden ratios !!
and angle of rotation t satifies the condition
sin(2t) = 2/(sqrt 5)
Heart-15a El-Milick, 1936
y = x(2/3) +- (sqrt (1-x2))
x 0 to 1 - sign applies for y < 0 region
x 1 to 0 + sign applies for y > 0 region
Heart-15b Kurt Eisemann
y = (3/4)*x(2/3) +- (sqrt (1-x2))
x 0 to 1 - sign applies for y < 0 region
x 1 to 0 + sign applies for y > 0 region
Heart16-A Hans Schupp, Heinz Dabrock Höhere Kurven, 1995
2 parameters p & q
In general x2 + 2*(y - p|x|q)2 = 1
or y = p|x|q +- sqrt (0.5*(1 - x2))
p = 3/5 , and q = 2/3
Heart-17 Heart Curve --ref. Math World
x = sin(t)cos(t)*ln(|x|)
y = cos(t)*√(|x|)
-1<= t <= 1
Heart-18 Heart Curve --ref. Torsten Sillke-rotated 90 °
r = (1 - |t-π/2| )(1 + 3|t - π/2| )
x = r*cos(t), y = r*sin(t)
right half (π/2 - 1) < t < π/2
left half π/2 < t < (π/2 + 1)
|
click here to enlarge (1) Heart #1  |
click here to enlarge (2) Heart #2 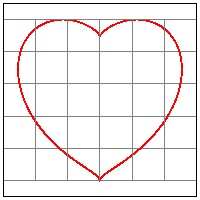 |
click here to enlarge (3) Heart #7 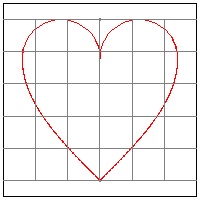 |
| click here to enlarge (4) Heart #8 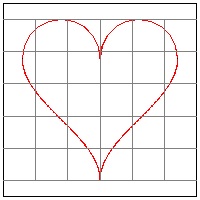 |
click here to enlarge (5) Heart #9 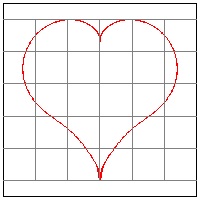 |
click here to enlarge (6) Heart #10 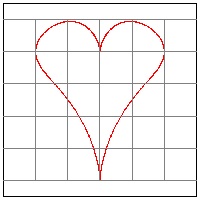 |
| click here to enlarge (7) Heart #11 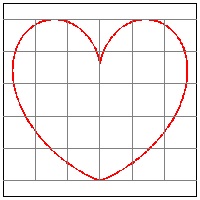 |
click here to enlarge (8) Heart #12 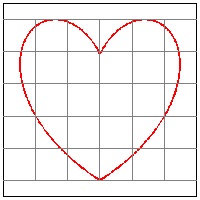 |
click here to enlarge (9) Heart #12A 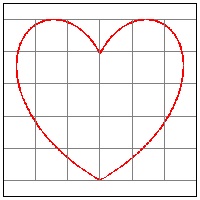 |
| click here to enlarge (10) Heart #13  |
click here to enlarge (11) Heart #14A 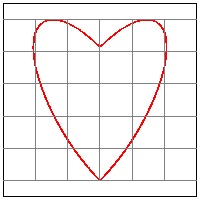 |
click here to enlarge (12) Heart #14B 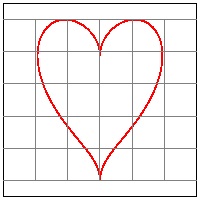 |
| click here to enlarge (13) Heart #14C 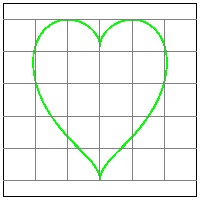 |
click here to enlarge (14) Heart #15A 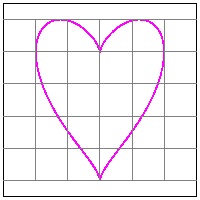 |
click here to enlarge (15) Heart #15B 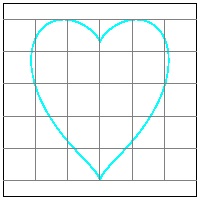 |
| click here to enlarge (16) Heart #16A 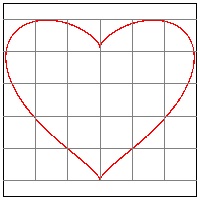 |
click here to enlarge (17) Heart #17 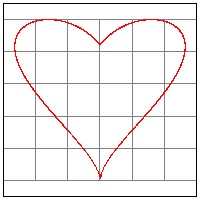 |
click here to enlarge (18) Heart #18 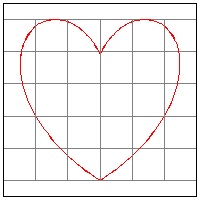 |
| click here to enlarge (19) Heart #19 3/4 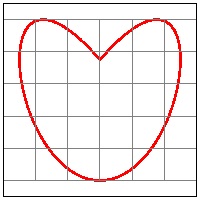 |
click here to enlarge (20) Heart #19 5/6 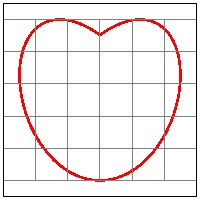 |
click here to enlarge (20) Heart #19 9/10 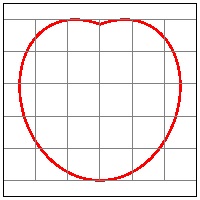 |
Finally
Your answer to "Red Heart Quiz"
One of the "Harmonograph heart" is the ideal heart shape we have been looking for.How the dissection is doen is showm below.
click here to get 800 x 500 image

********** Download this drawing(DWG format) **********
As explained in "4 arcs heart" section, a heart shape which qualifies to be used in "Red Heart Quiz" must have an ending arc at the bottom with its center located on the axis of symmetry. The critical point is to find evolute point to enable a smooth transition of tangent.
An exmaple is given in "4 arcs Heart".
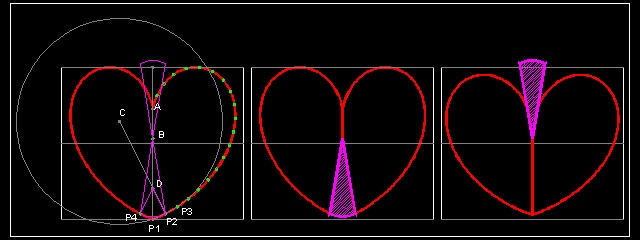
In general case, suppose the reader wants to accomplish the similar feat using a heart shape, say, "Heart #11" above.
It is necessasry to find out the evolute of this curve in the neighborhood of the bottom of the heart. One way to do it is to divide the curve into equal length interval, and find the center of the circle which passe through the 3 continuous points on the line. This will define the evolute point and evolute cruve connecting them..
example 1: Heart #11
Points P1,P2,and P3 are the first three points after the right half of the curve is divided into 20 equal length. In most CAD software , this is a standard option.
Point B is defined at (0, 0.55) , a bit higher than y = 0.5 line.
Then draw a circle passing through these 3 points. Its center point is "C".
Line connecting C to P2 cuts symmetry axis at point "D".
Find point P4 as a mirror image of point P2 wrt the vertical axis.
Draw an arc with its center at "D", from P2 ending at P4.
Wedge is defined by lines P2-B-P4 and an arc P2-P4.
click here to get 800 x 300 image
********** Download this drawing(DWG format) **********
A few more examples will be posted in the near future.
Files Download
All the files used to create this section can be downloaded to your computer in ZIPX file format.***** Download all Drawing (DWG format) files ***
***** Download all jpg image (*.jpg) files ***
***** Download all animation gif (*.gif) files ***
***** Download all program (LISP & VBA) files ***
References - Internet
In EnglishJürgen Köller Heart Curve
(Original was written in German. Translated into English)
Wikipedia Heart(symbol)
Eric W. Weisstein (MathWorld) Heart Curve
Nobuo Yamamoto (TDCC.LAB.SATELLITE) Heart Curves, Heart Curves II
(Original was written in Japanese. Translated into English)
In German
Jürgen Köller Herzkurve Spiralen
Hans-Jürgen (Matroids Matheplanet) Herzkurven
Hans-Jürgen Caspar Kurven
Torsten Sillke Herzkurven
In French
Robert Ferréol (mathcurve) 2-D Curves, Coeur de Raphaël Laporte
More informations about "One Cut Origami" In Japanese
One Cut Origami blog:: One Cut Origami (in Japanese)
References - Books
- Loyd, Samuel : Sam Loyd's Cyclopedia of 5000 Puzzles,Tricks & Conundrums with answers, first printing in New York in 1914, The Lamb publishing Co., Second Printing in 2007 by Ishi Press International. ISBN 978-0-923891-78-7
- Gardner, Martin.: Mathematical puzzles of SAM LOYD. Dover, 1959. The original was privately published in 1914 by Sam Loyd.
- Frederickson,Greg N.: Dissections: Plane & Fancy. ISBN 0-521-57197-9, Cambridge Univ. Press, 1997.
- Yates, Robert C.: A Handbbok On Curves and Their Properties. J.W.Edwards, Ann Arbor, 1947.
- Lockwood, E. H..: A Book of Curves. Cambridge University press., ISBN 0-521-05585-7, London, 1961.
- Tsukuda, Tsutomu: Curves (In Japanese) ISBN4-87472-189-3, Gendai Kougaku-sha,Tokyo, 1998.
- Yamamoto, Kousei: One-Cut Origami (in Japanese) Book I , ISBN4-89491-065-9,Houbun-sha ,Tokyo, 2004.
- Yamamoto, Kousei: One-Cut Origami (in Japanese) Book II , ISBN4-89491-090-X,Houbun-sha ,Tokyo, 2006.
- One Cut Origami blog:: One Cut Origami (in Japanese)
- Herrmann, Norbert: Mathematic is überall: ISBN 978-3-486-58243-7, Oldenbourg, München, 2007
- Ashton, Anthony: Harmonograph: A Visual Guide to the Mathematics of Music ISBN 0-8027-1409-9, Wooden Books, New York, 2003



























