Polygonal Medallion

Class-1 -- Floral Medallion --

In this class , we make three floral medallions using the papers provided. The final results and the diagrams used are shown below.

Fig.1-1 Final appearance
click to enlarge & print

Basic Twist Diagram

The diagrams are created by inserting the following twist fold pattern drawings on top of the flower images.
Notice that the paper to be used has a circular boundary.

Fig. 1-2A Hexagon Twist Diagram
click here to enlarge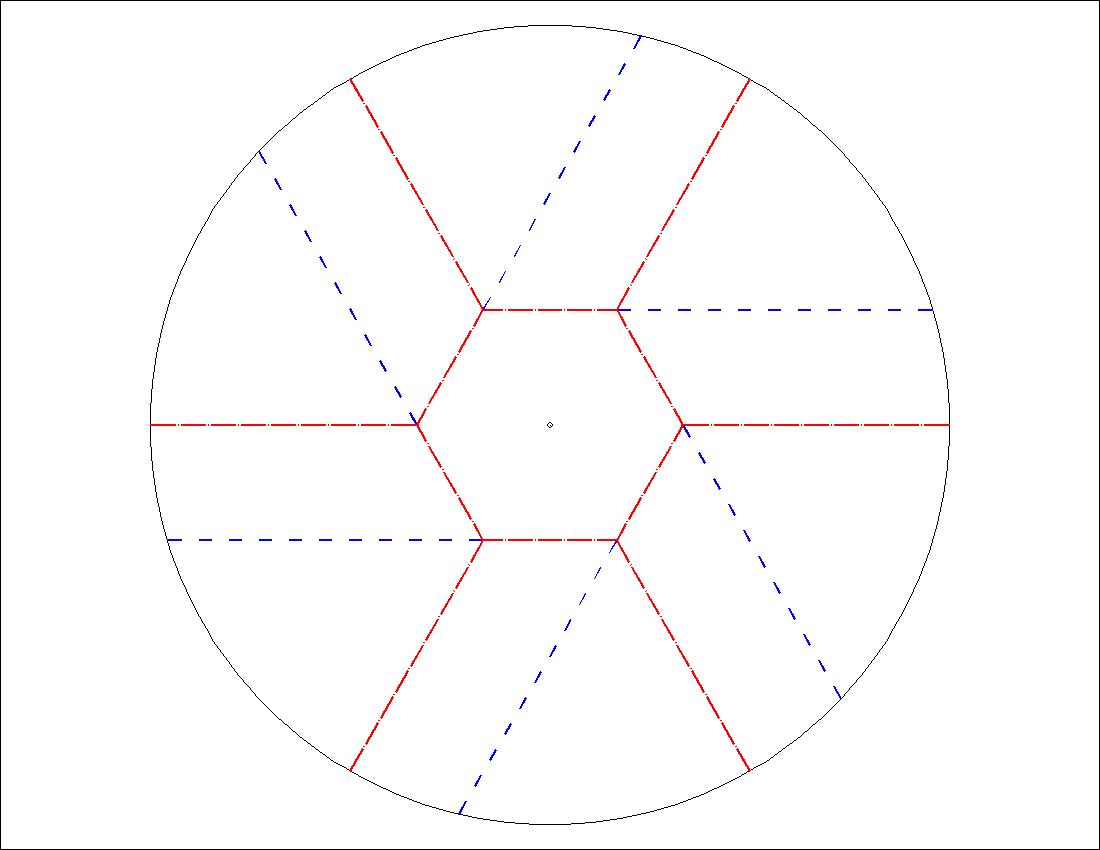

Fig. 1-2B Heptagon Twist Diagram
click here to enlarge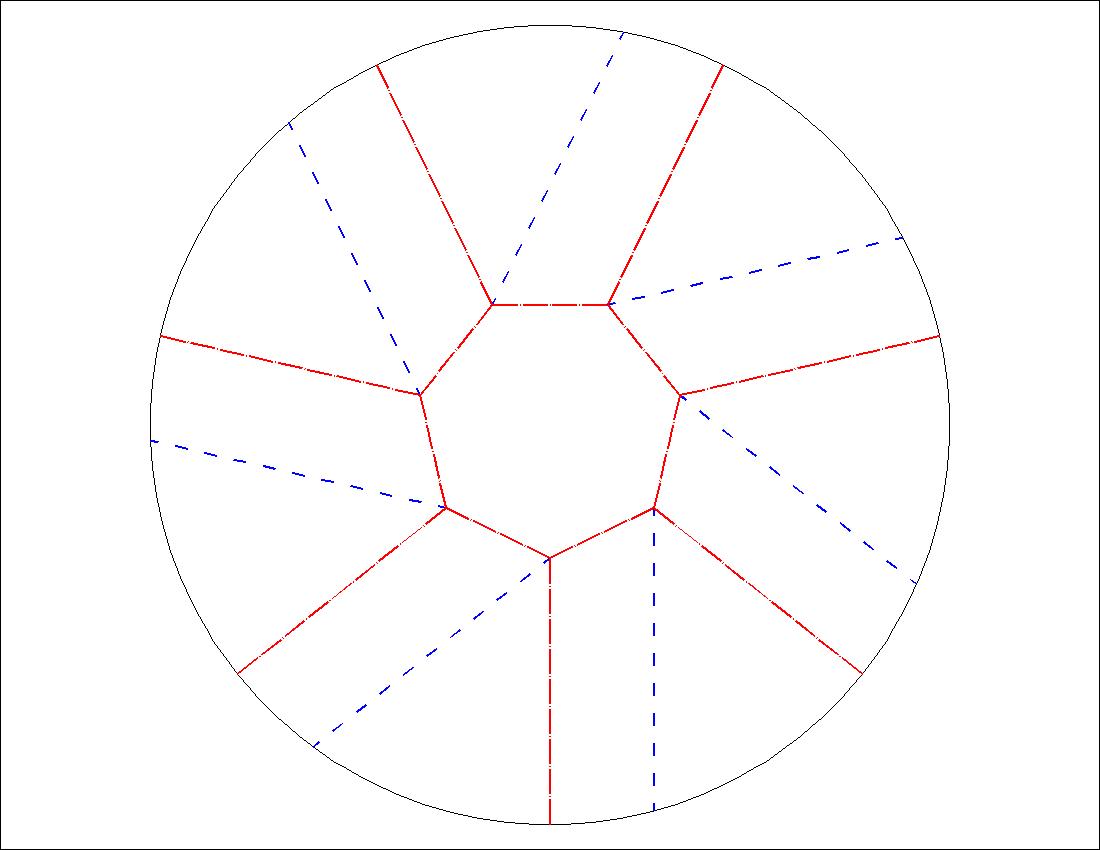

Flower image and its corresponding folding diagram

( 1 ) Example of a cluster of flowers

Fig. 1-3A Model 1 Flower image
click here to enlarge

Fig. 1-3B Model 1 Diagram
click here to enlarge

( 2 ) Example of a single flower1

Fig. 1-4A Model 2 Flower image
click here to enlarge

Fig. 1-4B Model 2 Diagram
click here to enlarge

(3) Example of a single flower2

Fig. 1-5A Model 3 Flower image
click here to enlarge

Fig. 1-5B Model 3 Diagram
click here to enlarge

Class - 2 -- Polygonal Medallion -Spirals --

In this class , we make two spiral medallions ,pentagon and hexagon , as shown below.

Fig. 2-1A Pentagonal Spiral
click to enlarge & print

Fig. 2-1B Hexagonal Spiral
click to enlarge & print

Pentagon spiral Model Pattern

The pentagonal spiral is made up of the multiple pieces shown below.

Fig. 2-2 Pentagonal spiral components
click here to enlarge


   The final bare minimum folding diagram and its dimensions are shown in the following figures.

  In the figure with dimensions, there are two center circles. Outer circle is the circle for the pentagon 

  resulted from folding , and the inner one is for the inscribing pentagon . The ratio is the reduction 

  scale factor.  The ratio  is 0.8416 (1.683 / 2.0)  for the pentagon case.  Then applying this ratio 

  repeatedly, we will have folding diagrams with constant reduction factor.

Pentagon Basic Pattern & Dimension

Fig. 2-3A Pentagon Basic Pattern
click to enlarge & print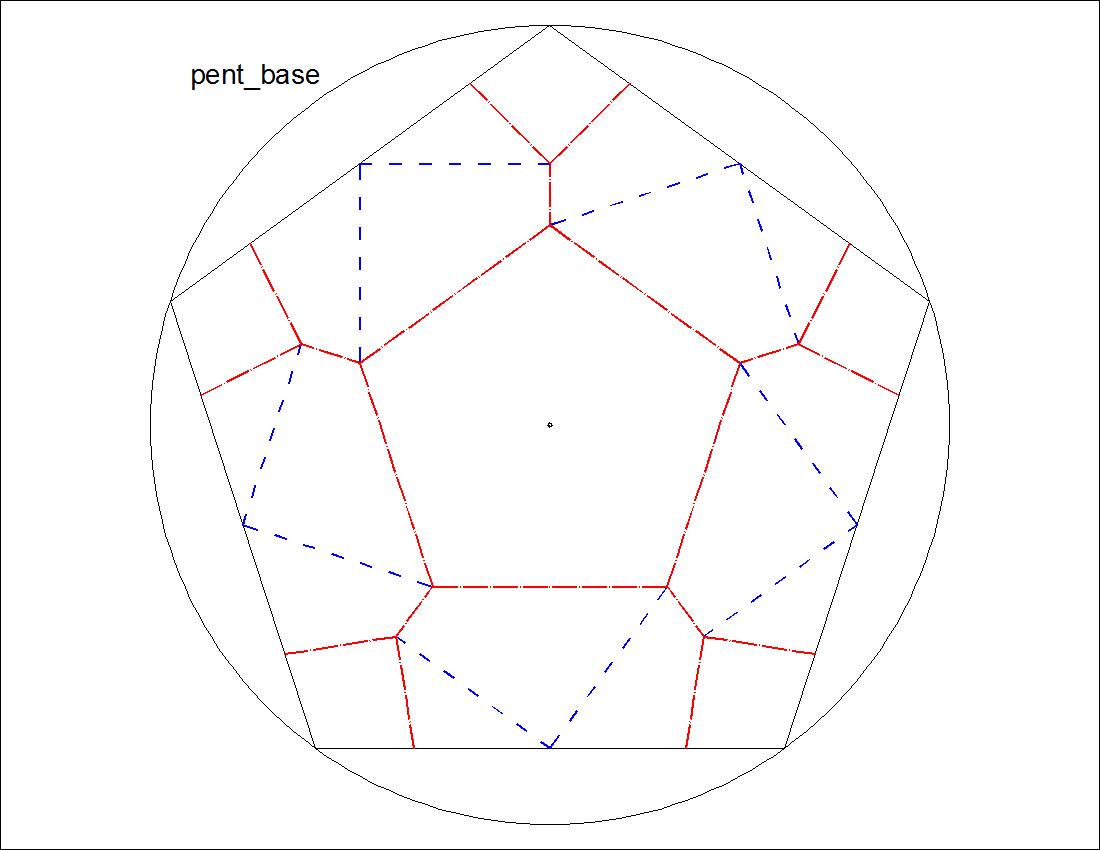

Fig. 2-3B Pentagon Basic Pattern Dimension
click to enlarge & print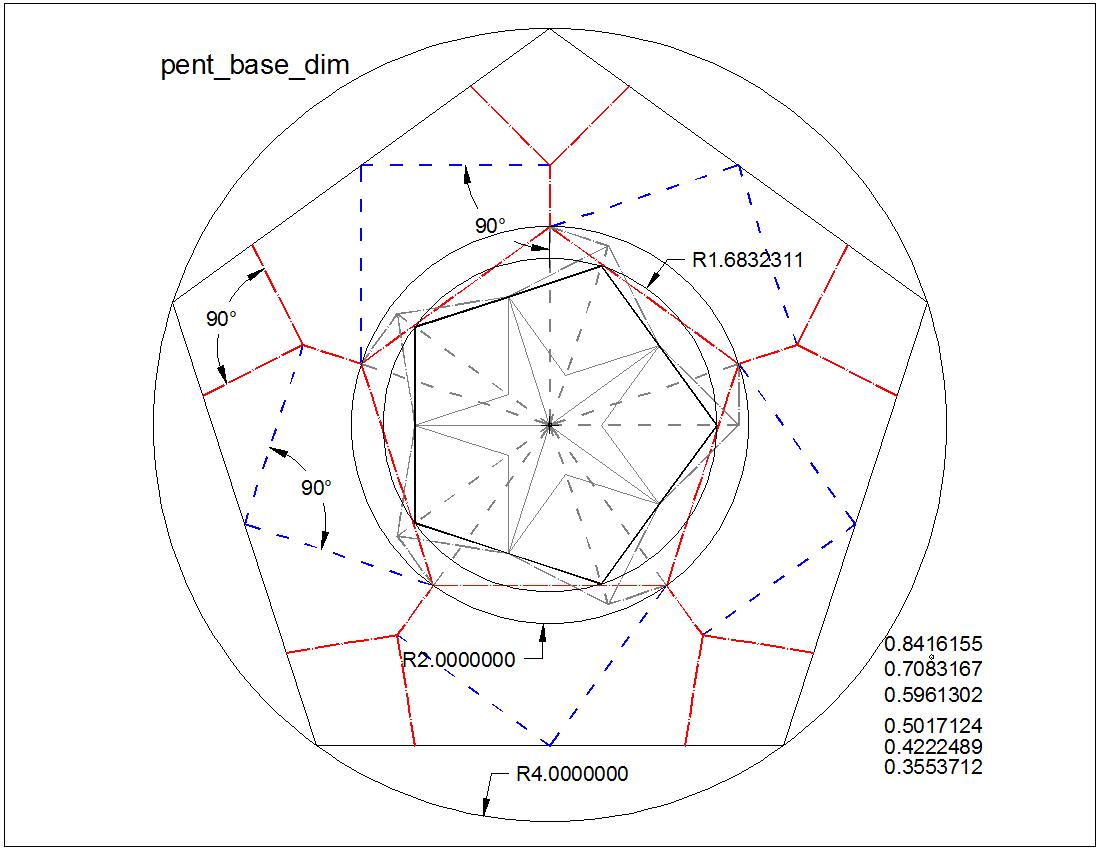

The diagrams are as follows:

Fig. 2-4A Pentagon pattern-00 click here to enlarge	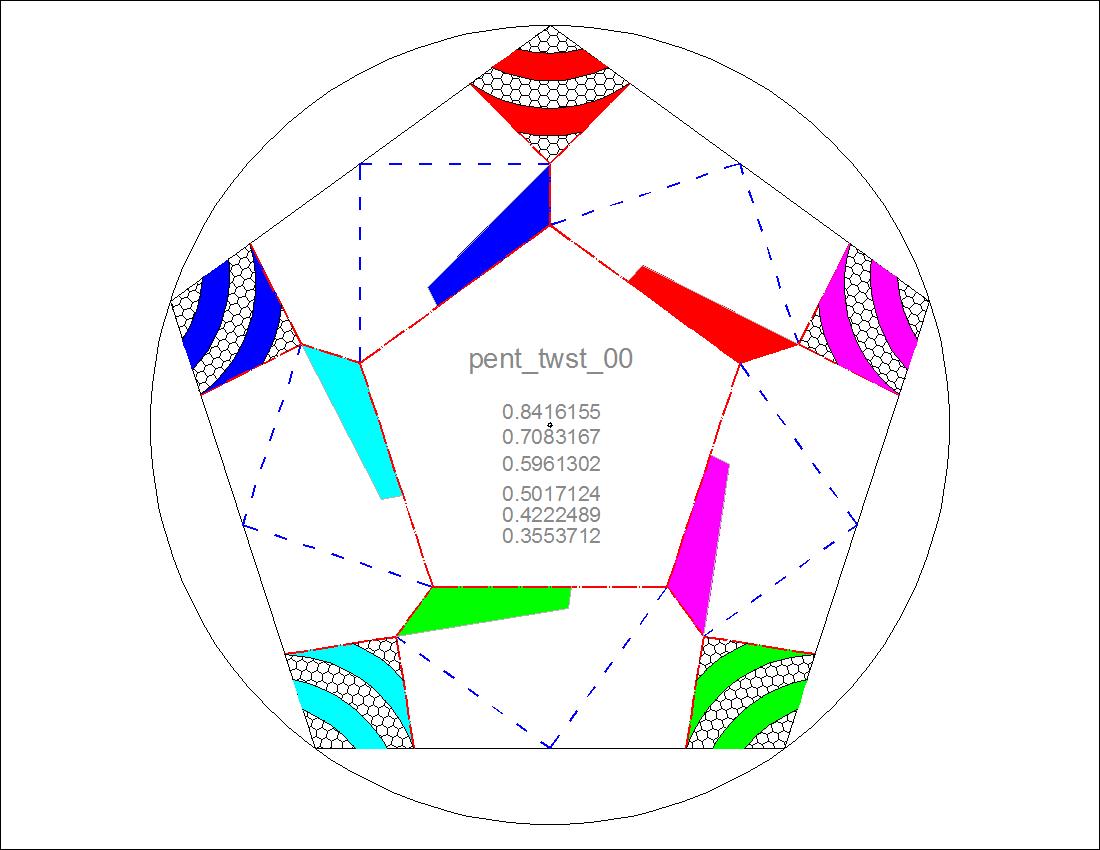Fig. 2-4B Pentagon pattern-16 click here to enlarge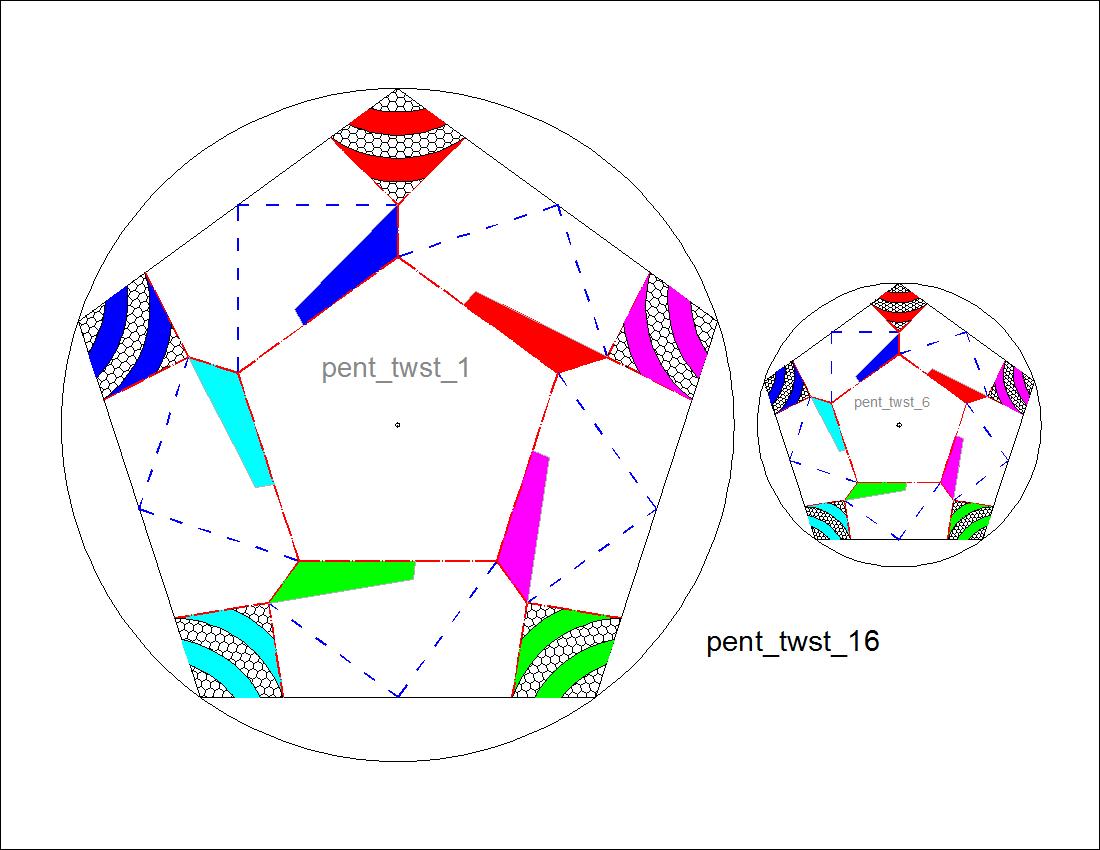
Fig. 2-4C Pentagon pattern-25 click here to enlarge	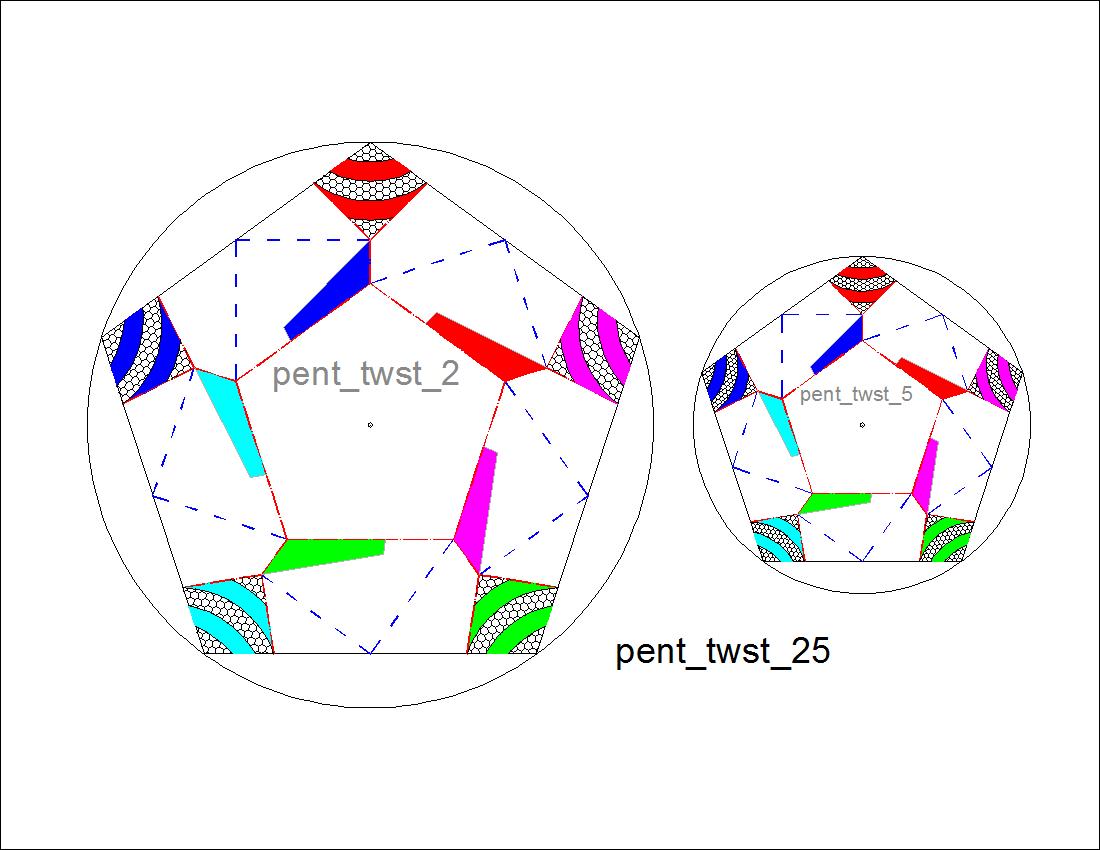Fig. 2-4D Pentagon pattern-34 click here to enlarge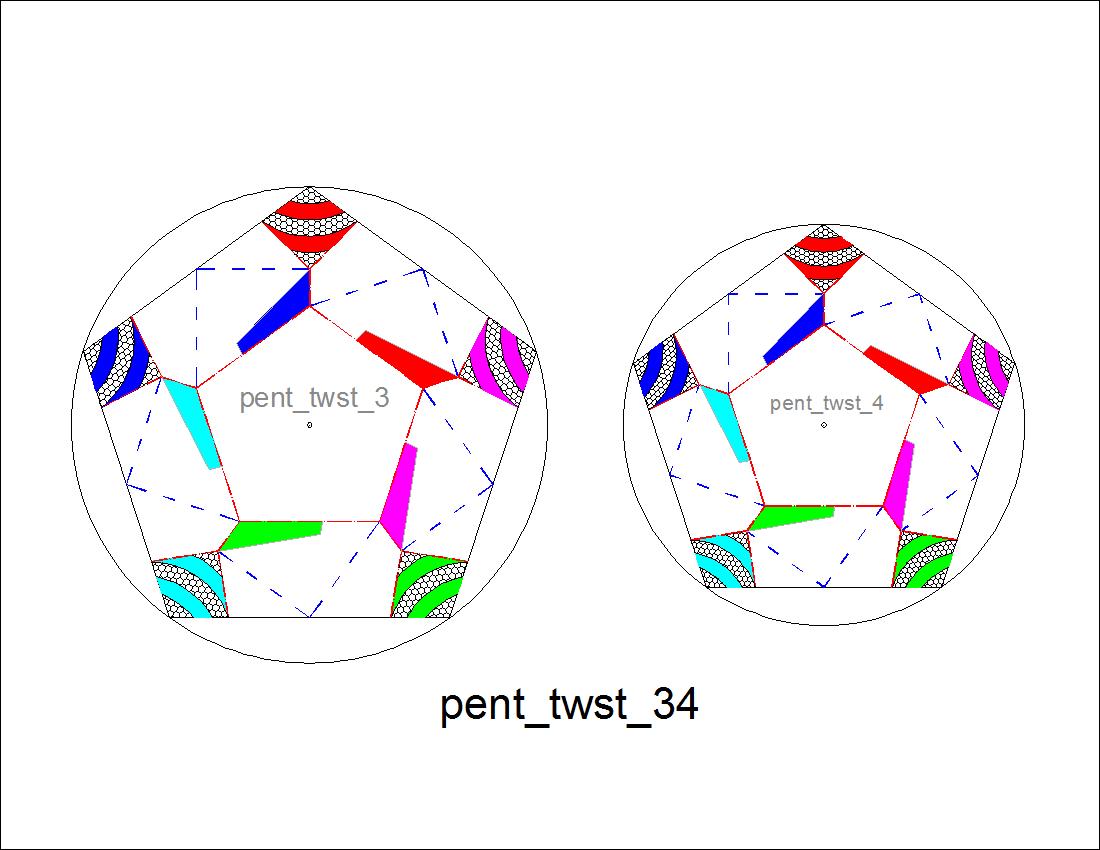

Hexagon Spiral Model Pattern

The hexagonal spiral is made up of the multiple pieces shown below.

Fig. 2-5 Hexagonal spiral components
click here to enlarge


       The final bare minimum folding diagram and its dimensions are shown in the following figures.
     In the figure with dimensions, there are two center circles. Outer circle is the circle for the hexagon 
     resulted from folding , and the inner one is for the inscribing hexagon . The ratio is the reduction 
     scale factor.  The ratio  is 0.73205 (1.464 / 2.0) for the hexgon case. Then applying this ratio 
     repeatedly , we will have folding diagrams with constant reduction factor.

Fig. 2-6A Hexagon Twist Base
click to enlarge & print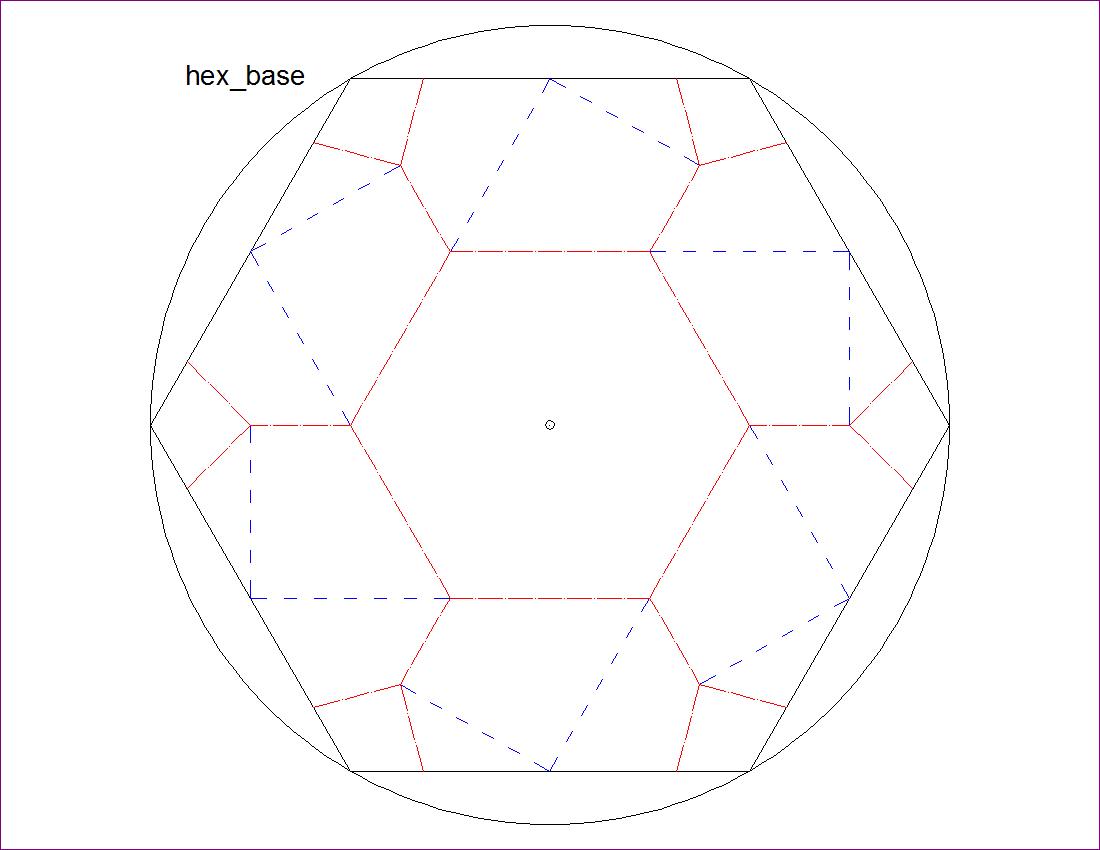

Fig. 2-6B Hexagon Twist Basic Dimension
click to enlarge & print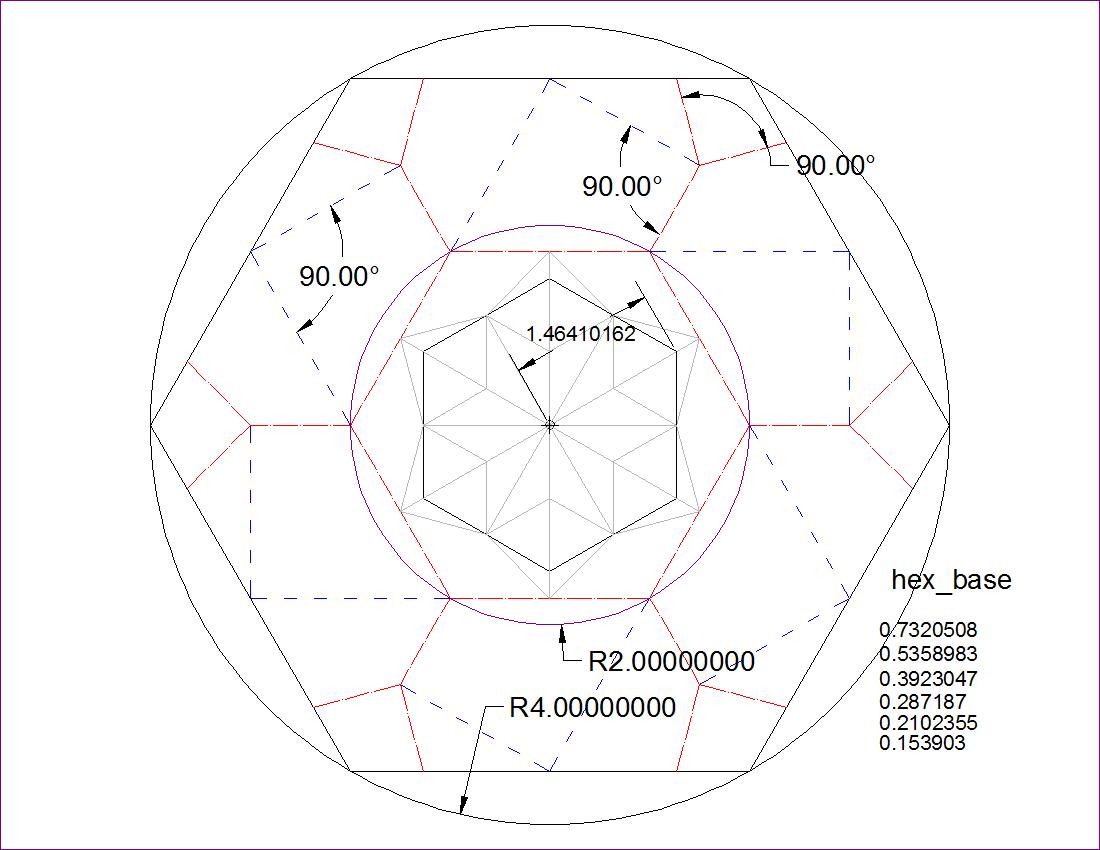

The diagrams are as follows:

Fig. 2-7A Hexagon Pattern-00 click here to enlarge	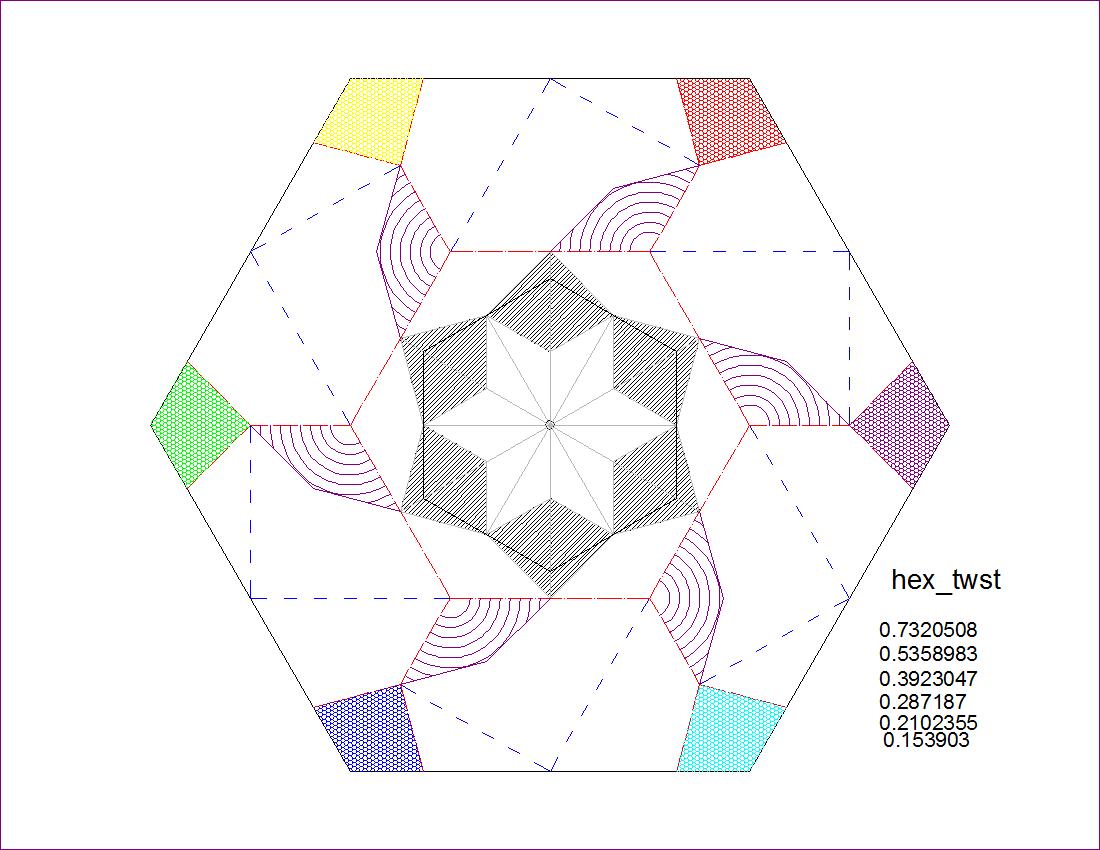Fig. 2-7B Hexagon Pattern-12 click here to enlarge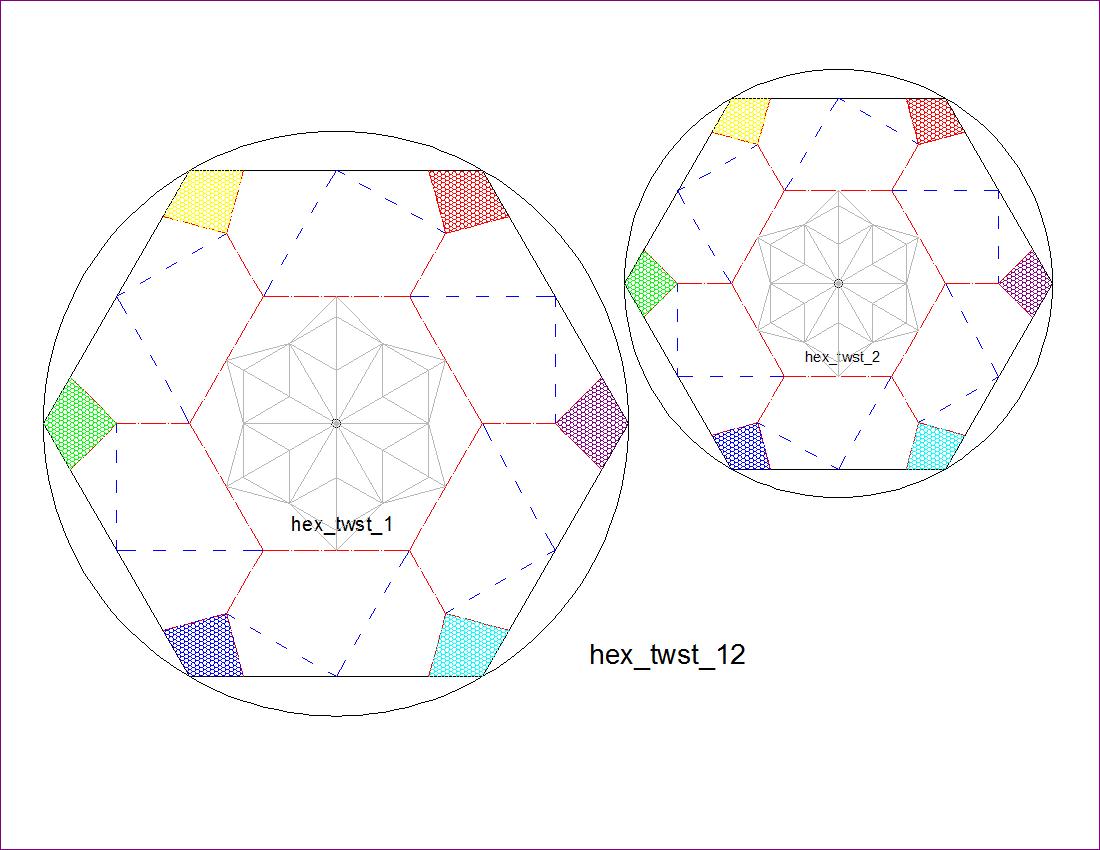
Fig. 2-7C Hexagon Pattern-3456 click here to enlarge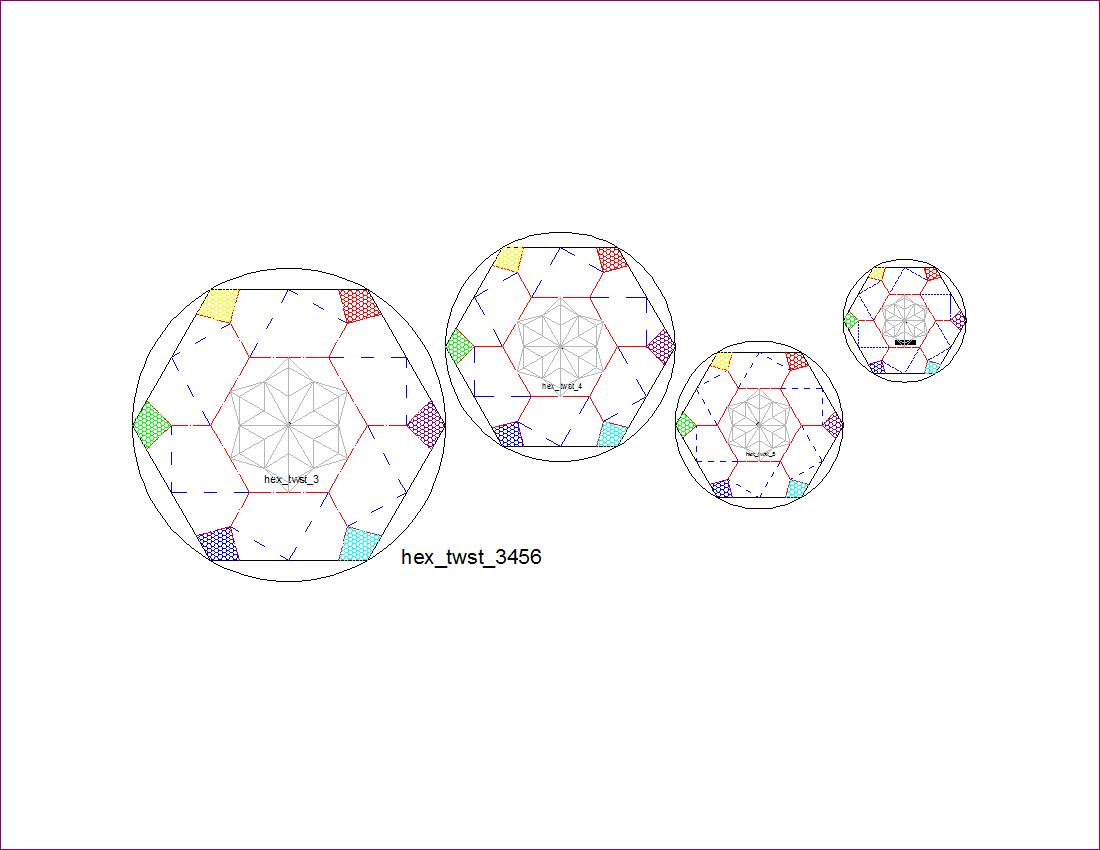

Class - 3 -- CAD Usage for Twist Fold --

Fig. 3-1A Model (I)
click to enlarge & print

Fig. 3-1B Model (II)
click to enlarge & print

There are 2 basic ways to accomplish "Twist Fold" though there are many variations based on them.
Here, as an exmple, a regular pentagon is chosen for the purpose of discussion, but the same idea
can be applied to any "N"-gons. Two pentagons, outer and inner, are arranged so that the line connecting the center point
and each apex of the inner pentagon passes through ,either the apex of the outer pentagon (Type-II) or
the mid-point of the outer pentagon's side (Type-I).
We also observe that in both cases angles are divided into 4 equal parts, at each mid-point of the side (Type-I)
or at each apex (Type-II).
So the each angle is
Type-I 180/4 = 45 degrees
Type-II 108/4 = 27 degrees
Typical diagrams and their dimensions are shown in the following figures.

Fig.3-2A Type-I Dimension
click to enlarge & print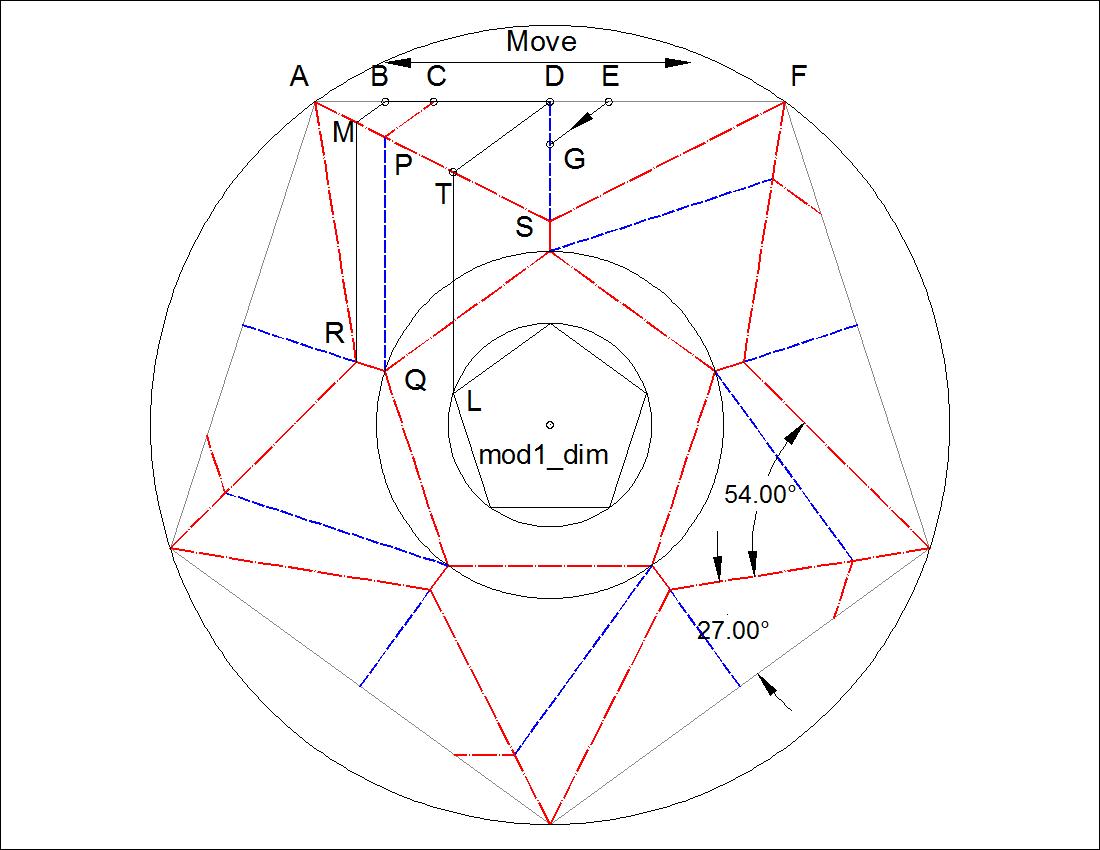

Fig. 3-2B Type-II Dimension
click to enlarge & print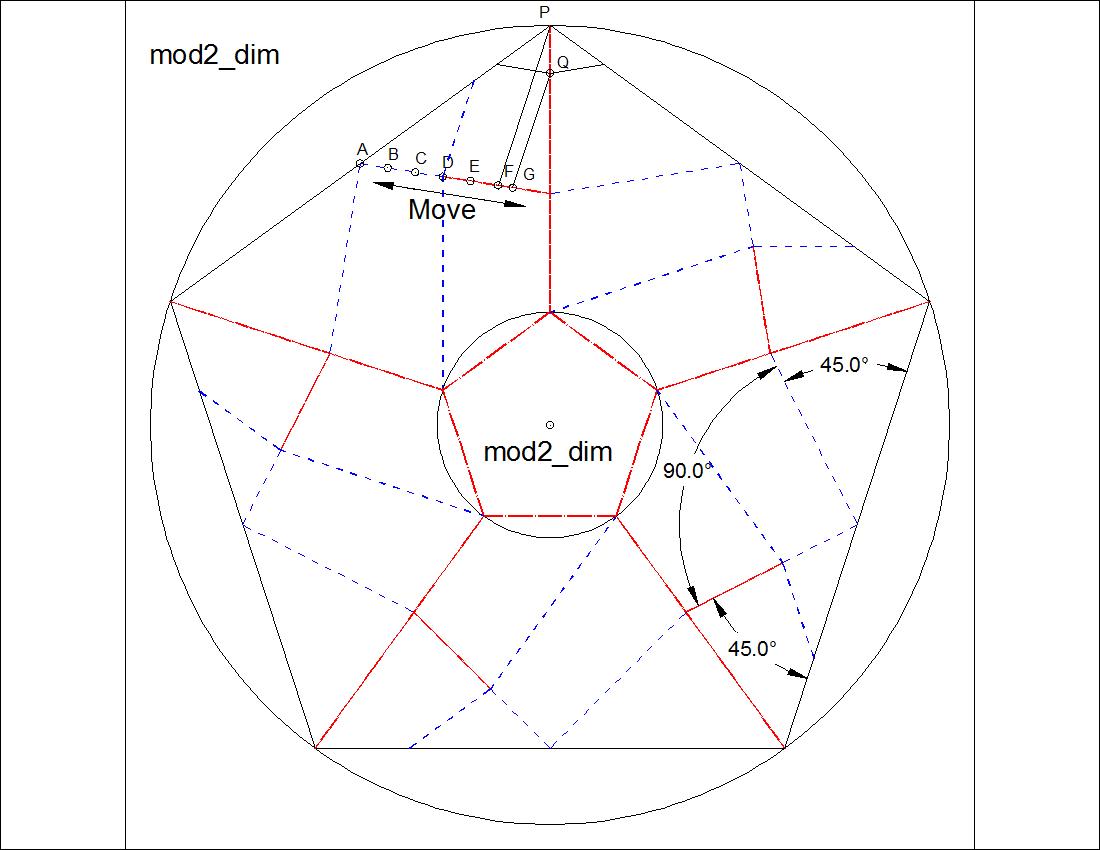

Using the dimensional drawing above, it is possible to create folding diagrams for multiple values of radii
of circles circumscribing the inner pentagons. The results are shown below.

Type-I Twist

Fig. 3-3A Type-I Group-Front Face
click to enlarge & print

Fig. 3-3B Type-I Group-Back Face
click to enlarge & print

Diagrams for Type-I Group

Fig. 3-4A Type-I "B" diagram
click to enlarge & print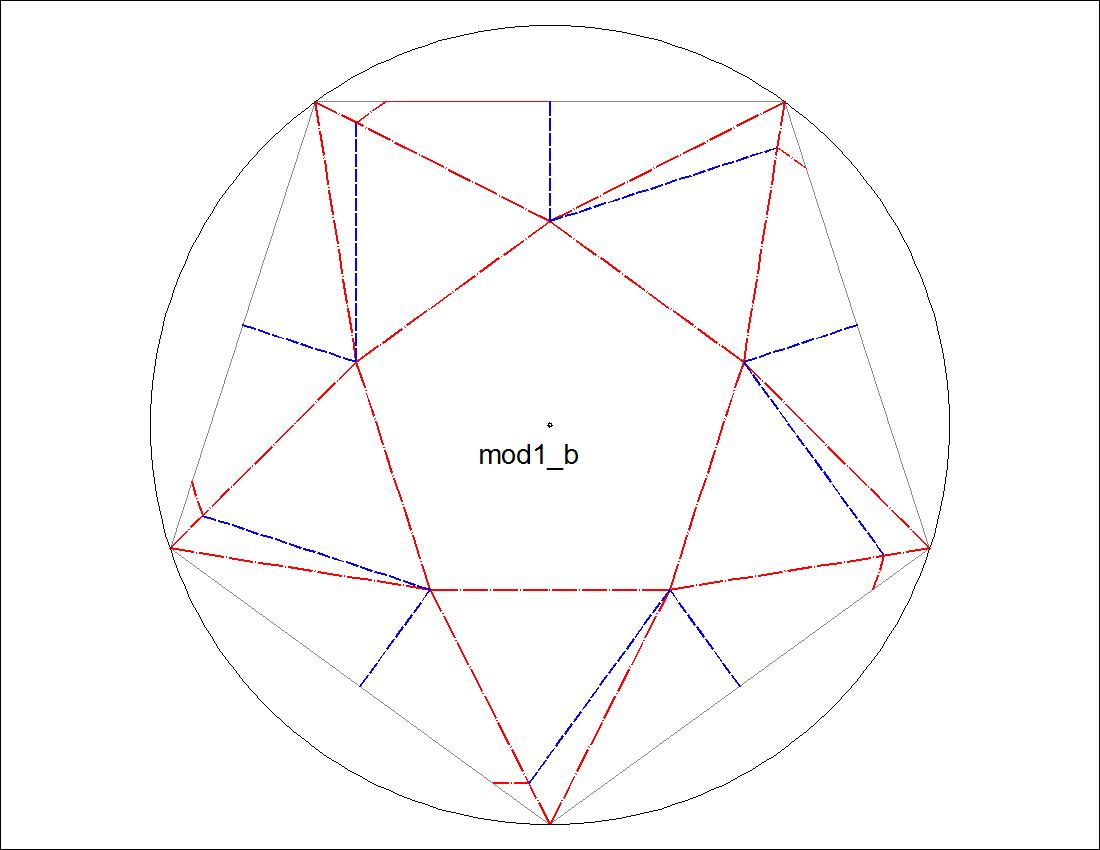

Fig. 3-4B Type-I "C" diagram
click to enlarge & print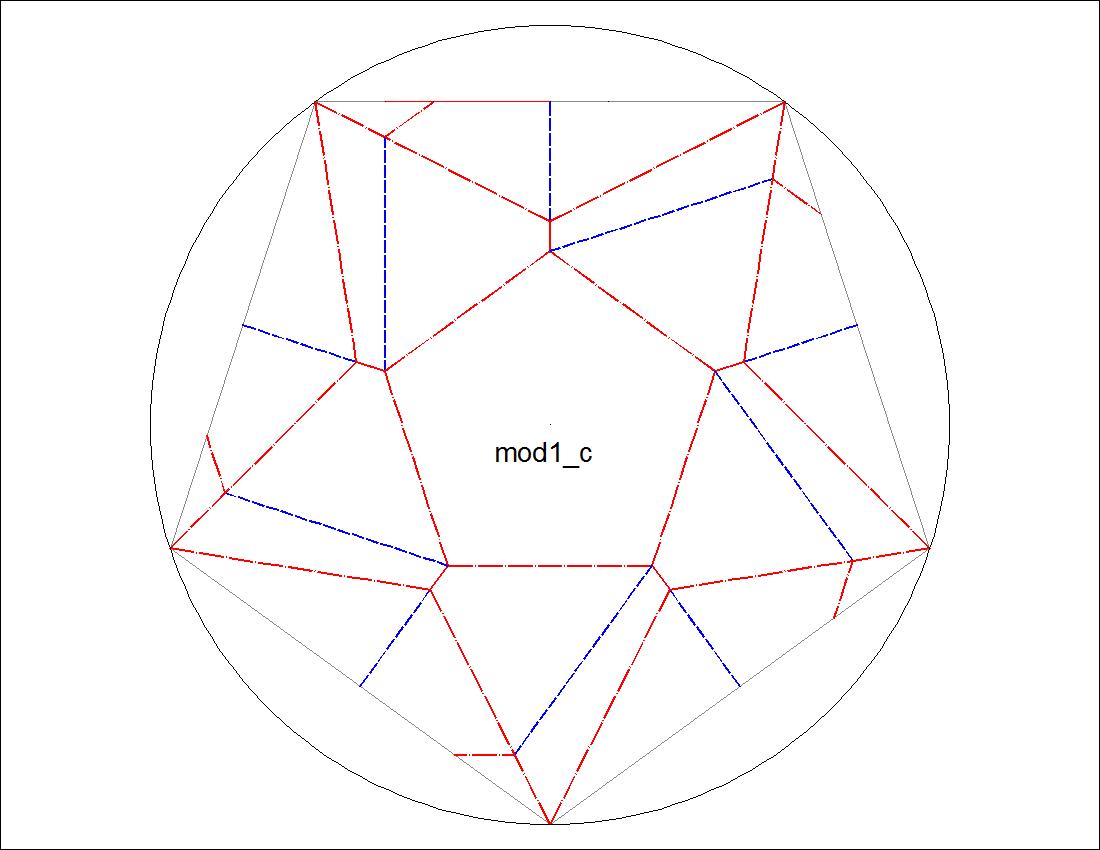

Fig. 3-4C Type-I "D" diagram
click to enlarge & print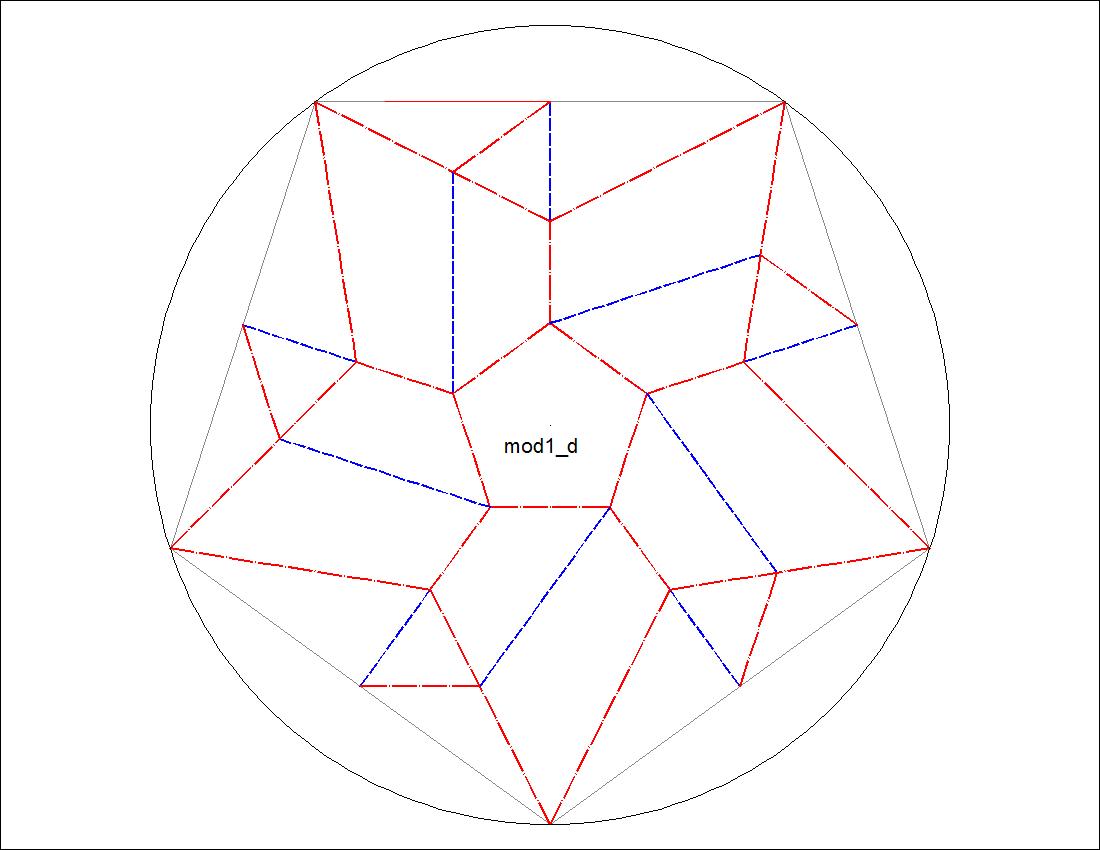

Fig. 3-4D Type-I "E" diagram
click to enlarge & print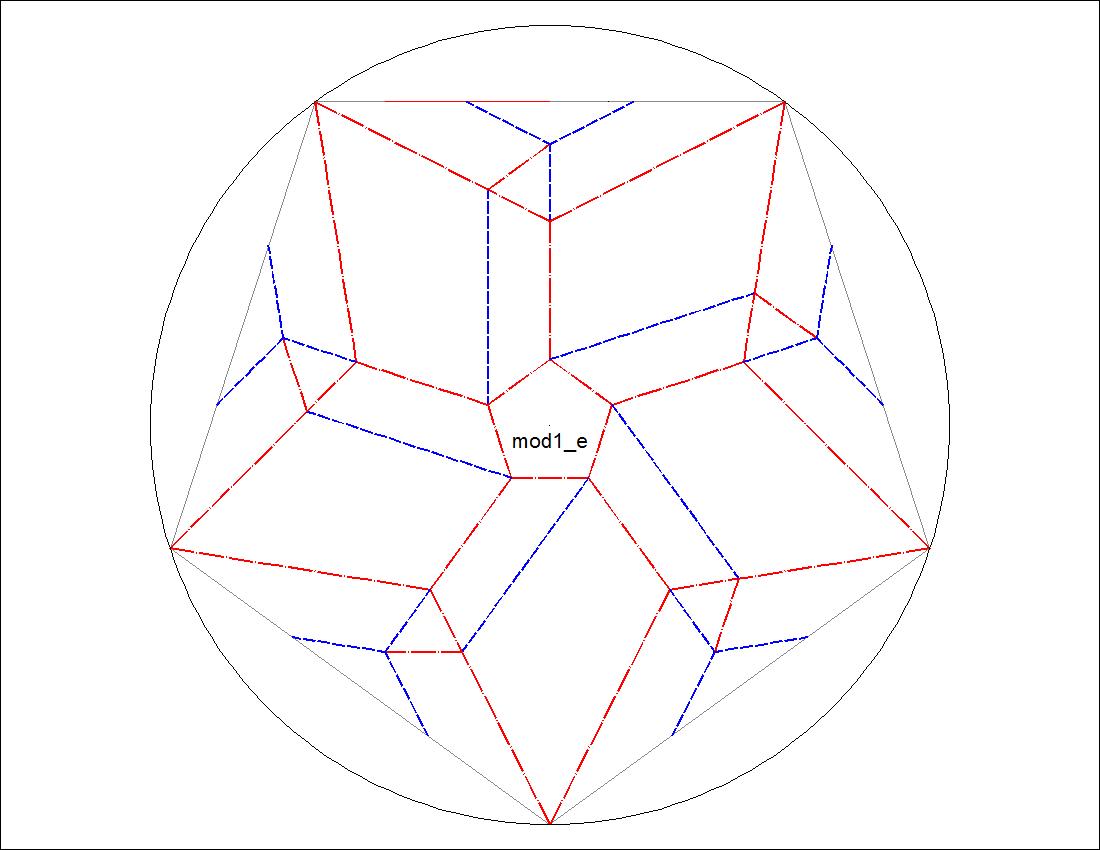

Type-II Twist

Fig. 3-5A Type-II Group-Front Face
click to enlarge & print

Fig. 3-5B Type-II Group-Back Face
click to enlarge & print

Diagrams for Type-II Group

Fig. 3-6A Type-II "B" diagram
click to enlarge & print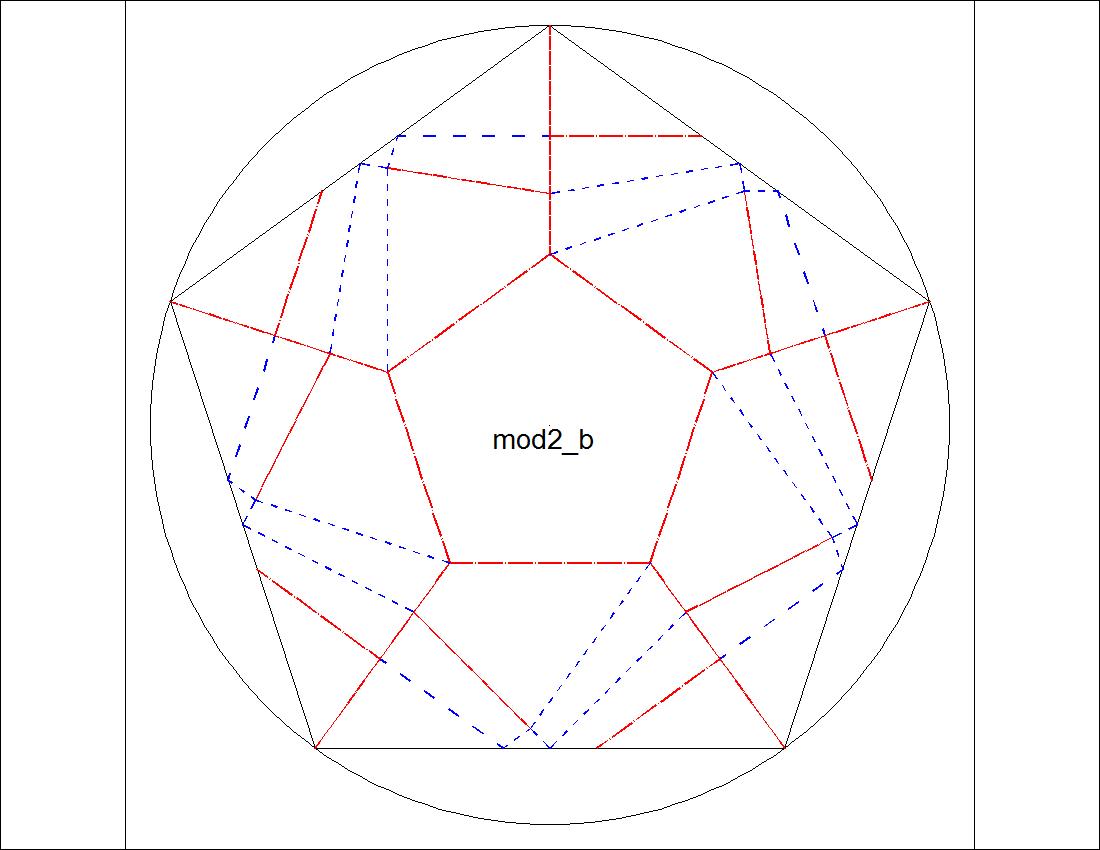

Fig. 3-6B Type-II "C" diagram
click to enlarge & print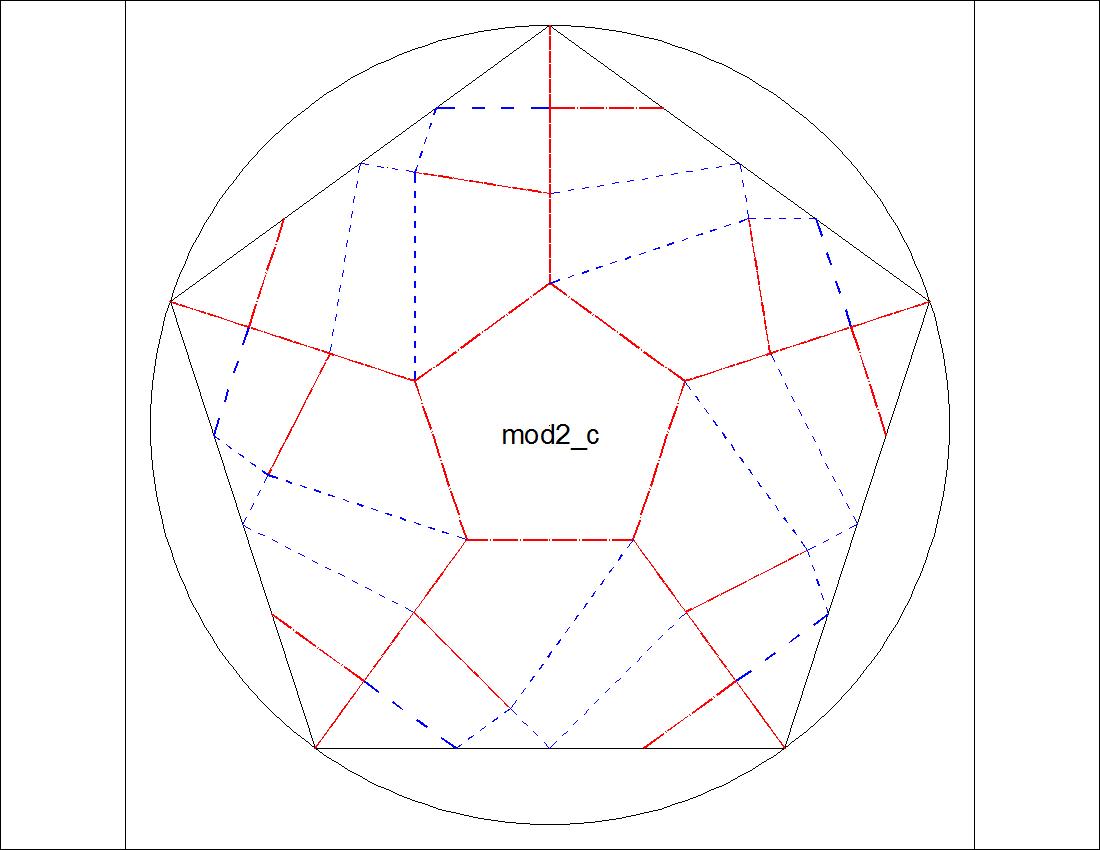

Fig. 3-6C Type-II "D" diagram
click to enlarge & print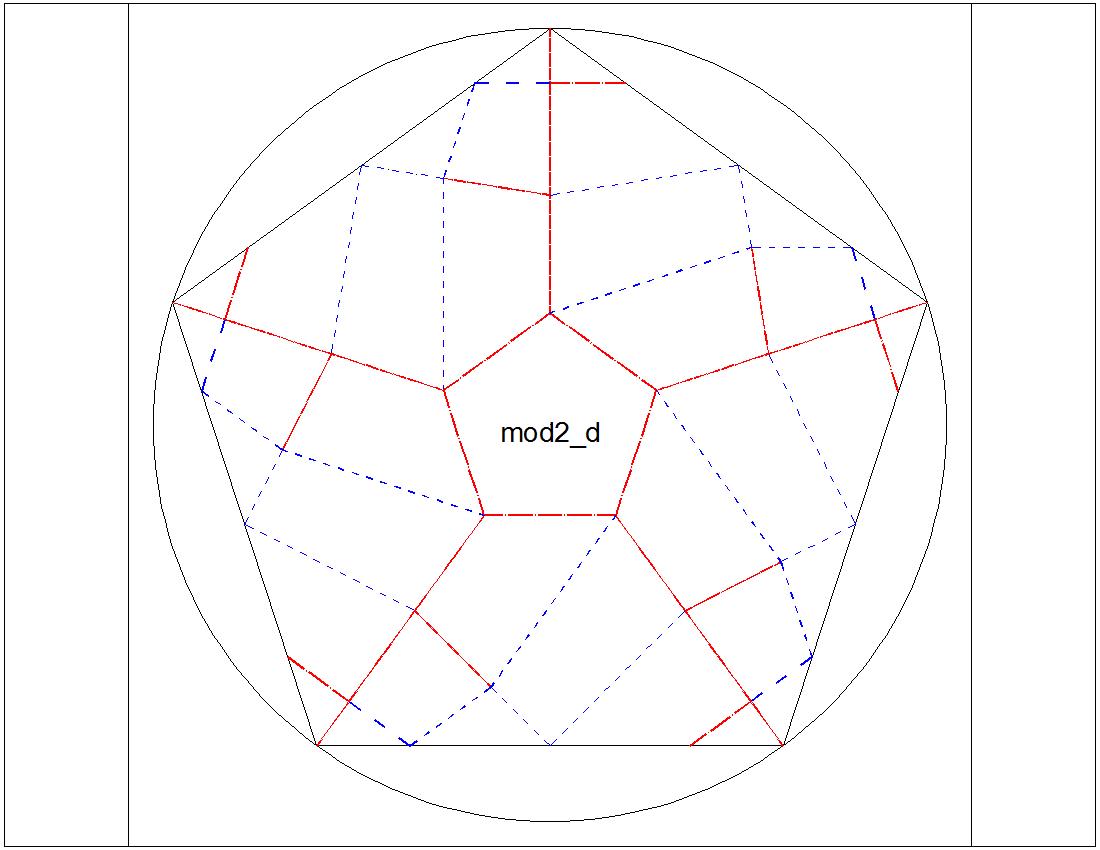

Fig. 3-6D Type-II "E" diagram
click to enlarge & print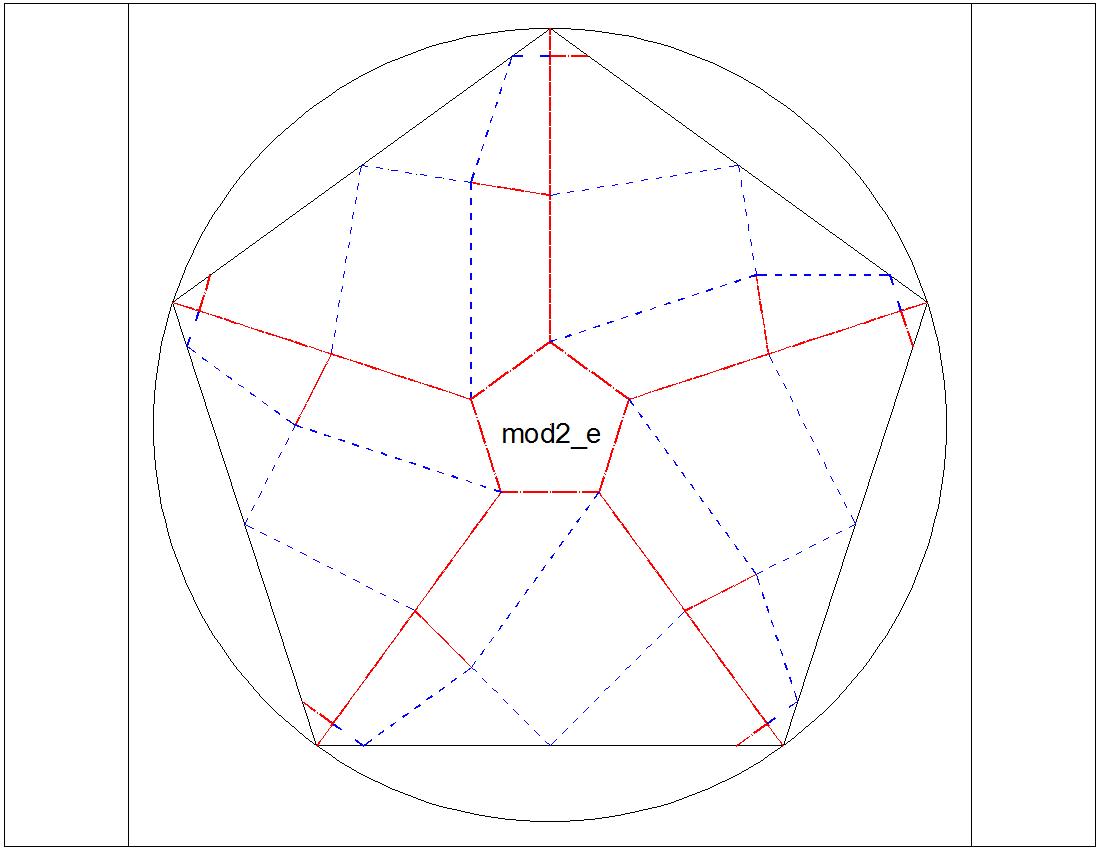

Fig. 3-6E Type-II "F" diagram
click to enlarge & print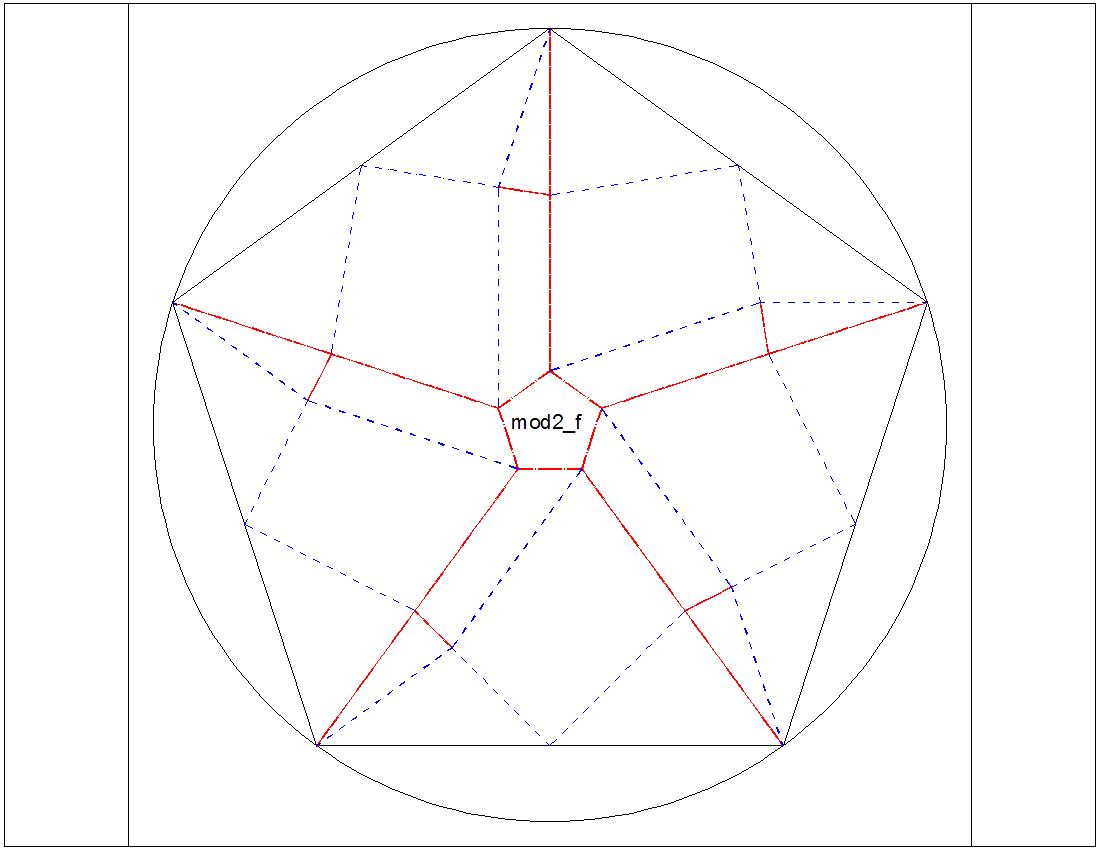

Fig. 3-6F Type-II "G" diagram
click to enlarge & print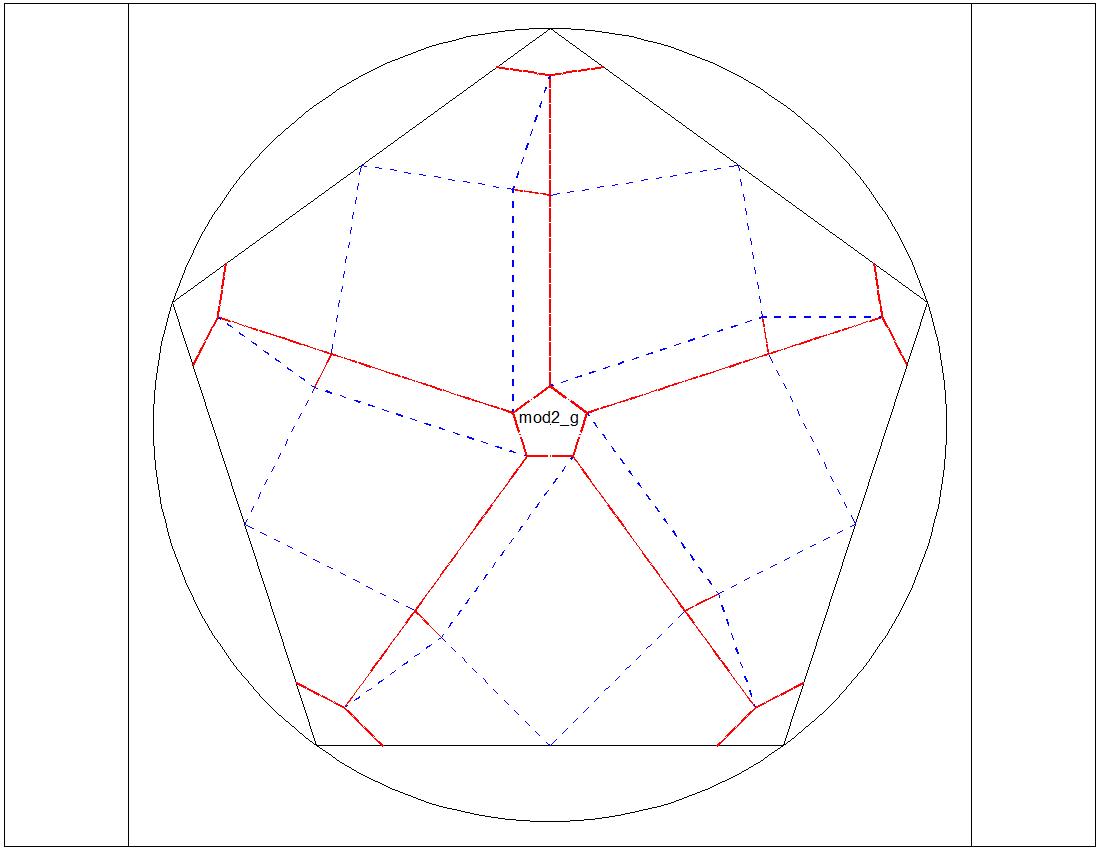

  

Observing these 2 figures,we notice that

1. In Type -I, somewhere between "C" and "D" ,the radii of the base pentagon and five-pointed-star
    become identical.

2. In Type - II, between "F" and "G", the red colored tip  will be partially hidden under the center pentagon.


How can we find the exact location ?

Model - I

Fig. 3-7A Dimension for "B" & "D"
click to enlarge & print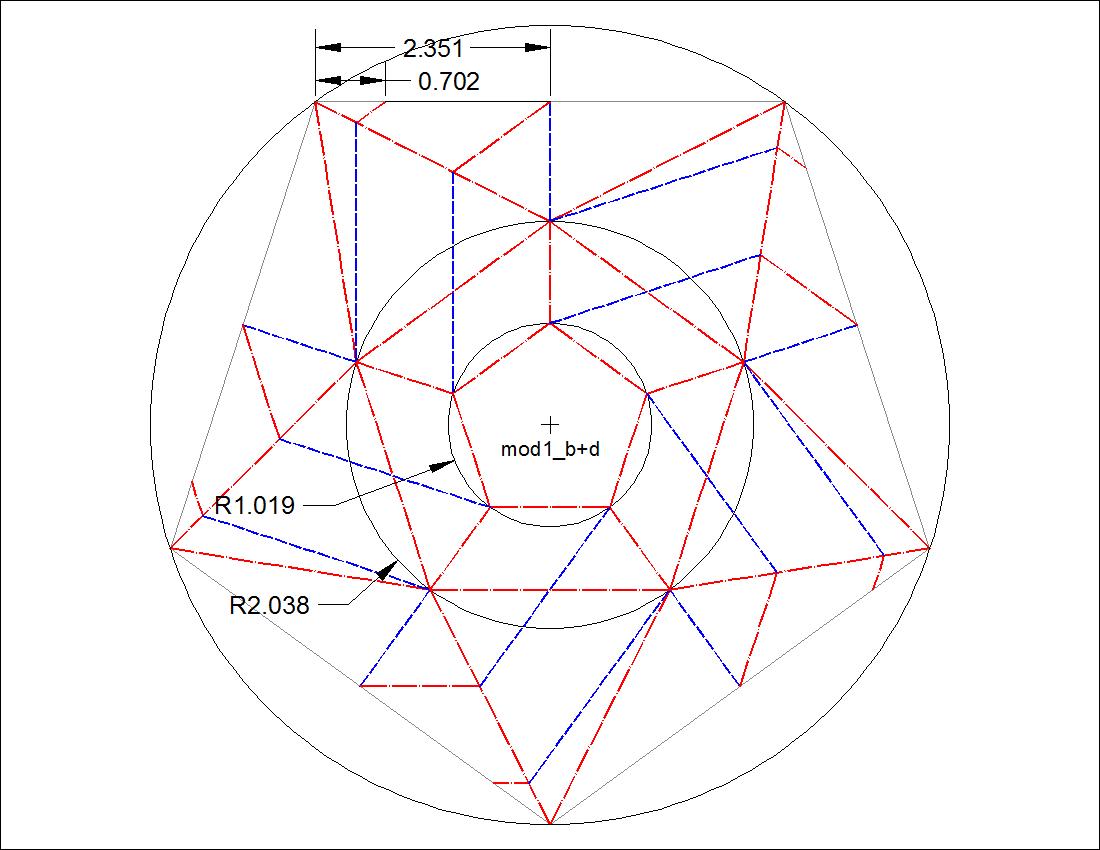
mod1_b+d.jpg

Fig. 3-7B Parameter Graph
click to enlarge & print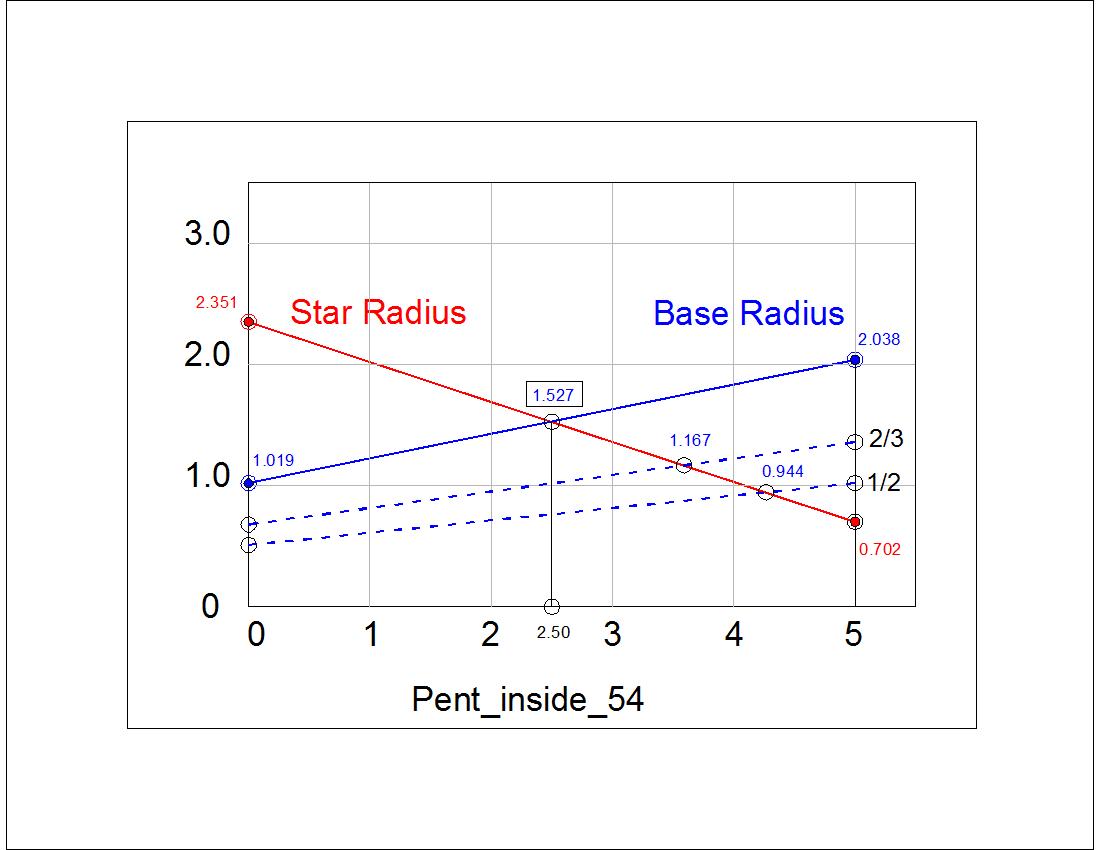


 The diagrams for case "B" and "D" are drawn on the same drawing.

     In the drawing,                            "B"        "D"

	      radius of the Star  :            0.702      2.351
 
              radius of the base pentagon  :   2.038      1.019

  This set of data are plotted as a graph , Star Radius ( red ) and Base Radius ( blue ).

 Two lines intersects at radius = 1.527, this is the radius of the diagram to be used.

 A new diagram is created and this is pasted over the separately prepared image file.

 Both are shown in the figures below.

Fig. 3-8A Model-I base diagram
click to enlarge & print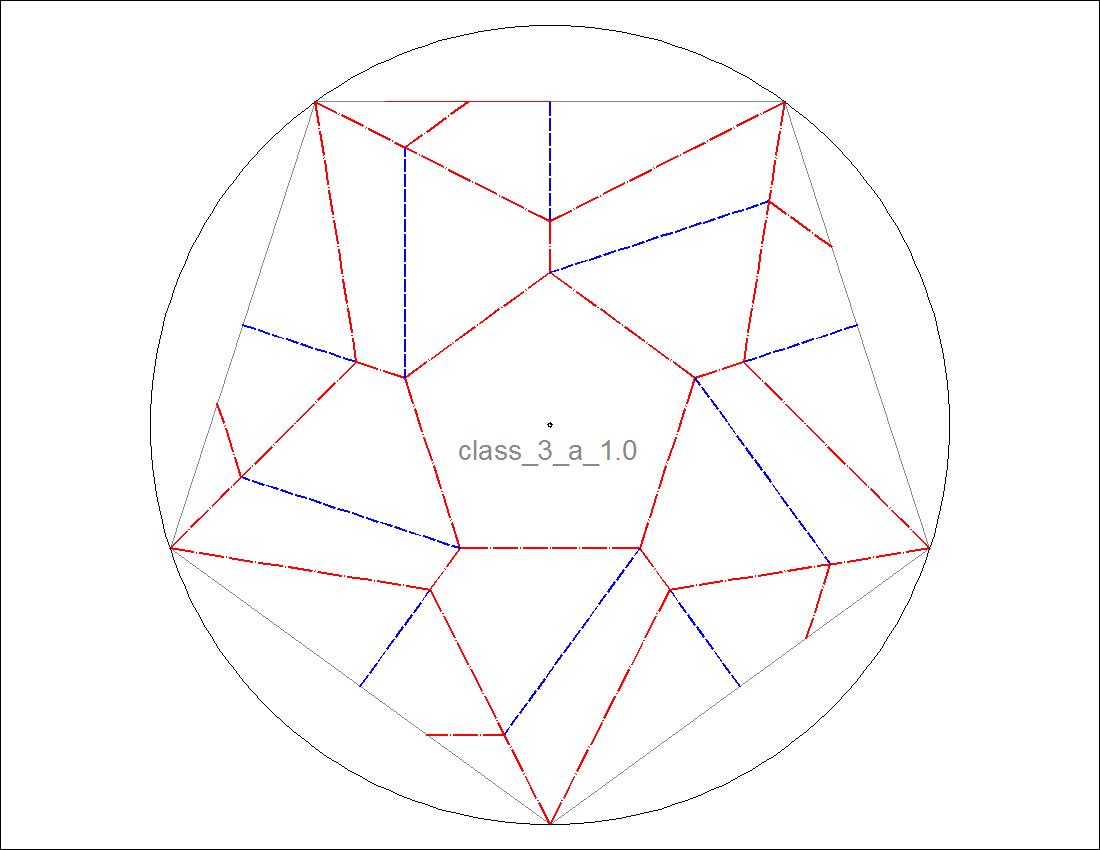
class_3_a_1.0.jpg

Fig. 3-8B Model-I Diagram
click to enlarge & print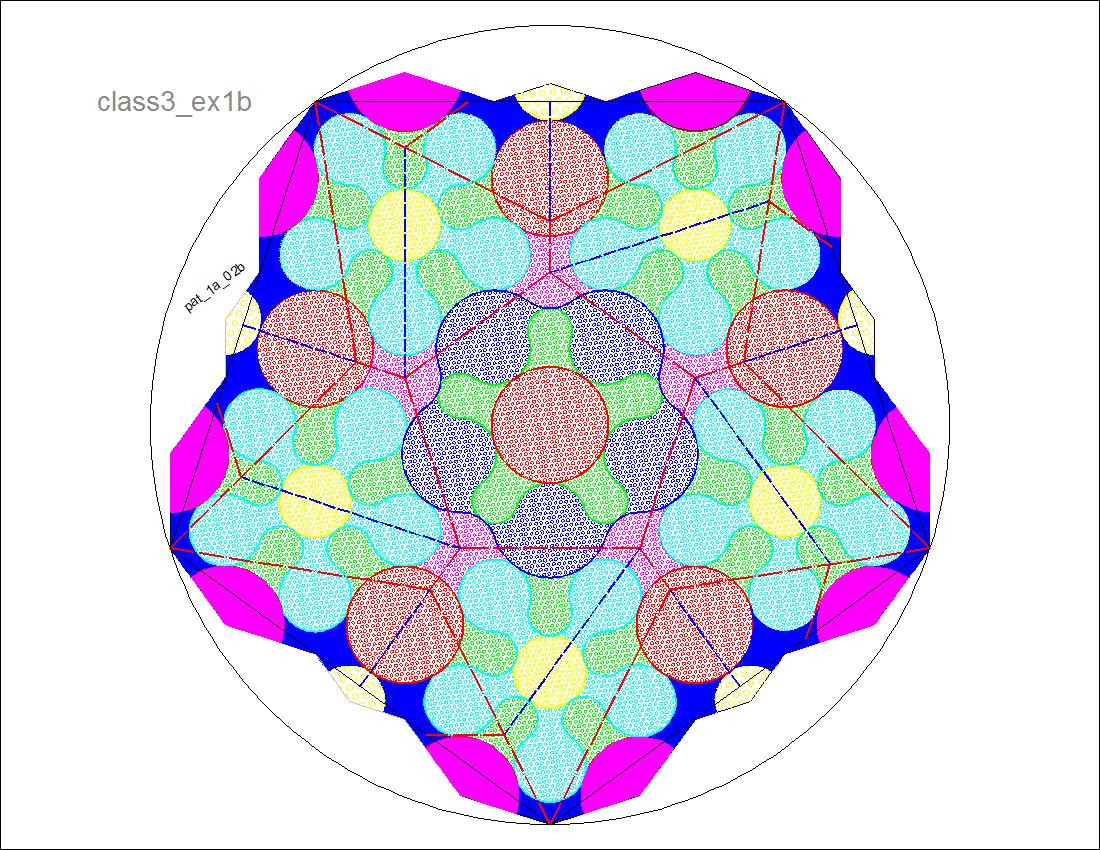

Model - II

Fig. 3-9A Dimension for "F" & "G"
click to enlarge & print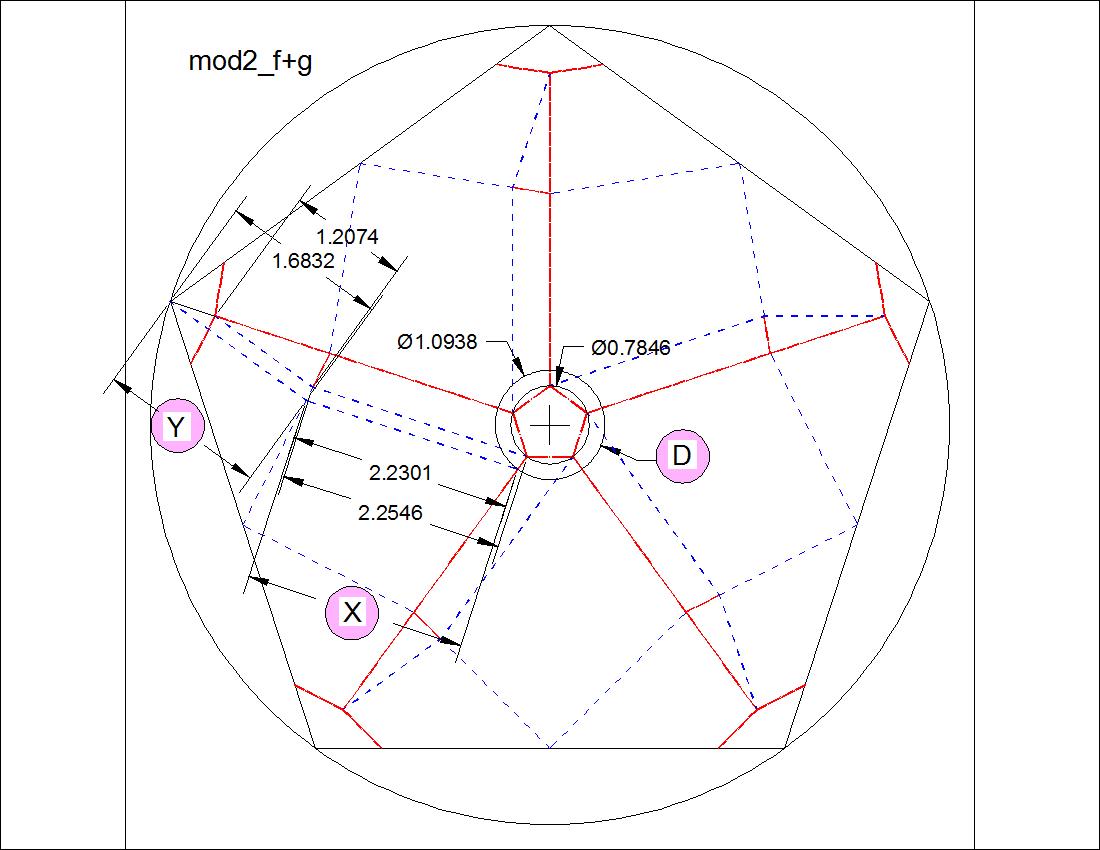
mod2_f+g.jpg

Fig. 3-9B Parameter Gra[h
click to enlarge & print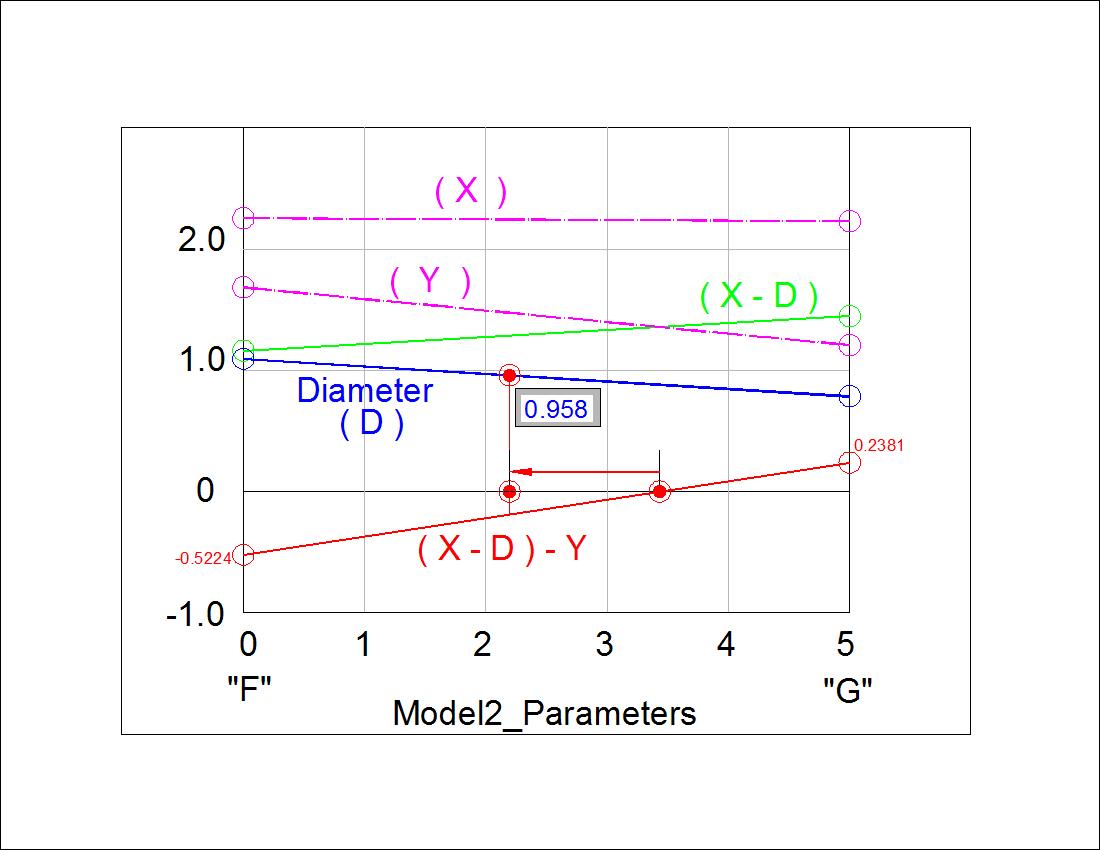


 The diagrams for case "F" and "G" are drawn on the same drawing.

     In the drawing,                               "F"        "G"

	     length of "X"   :                   2.2546      2.2301 

              length of "Y"  :                   1.6832      1.2074

	     diameter of the base pentagon       1.0938      0.7846

              ( X - D)                           1.1608      1.4455

              ( X - D) - Y                      -0.5224      0.2381

  This set of data are plotted in a graph , parameters shown in different colors.

 Note the values of ( X - D) - Y.  They are the distance of overlapping we are looking for. 

 The point where RED colored line intersects with ordinate value = 0 is the point 

where the tip of the star touches the base pentagon. 

 For the actual choice of base pentagon dimension, this point is moved slightly

to the left to be safe.  Its value is 0.958. The diagram using this diameter is shown below.

Fig. 3-10 Model-II base
click to enlarge & print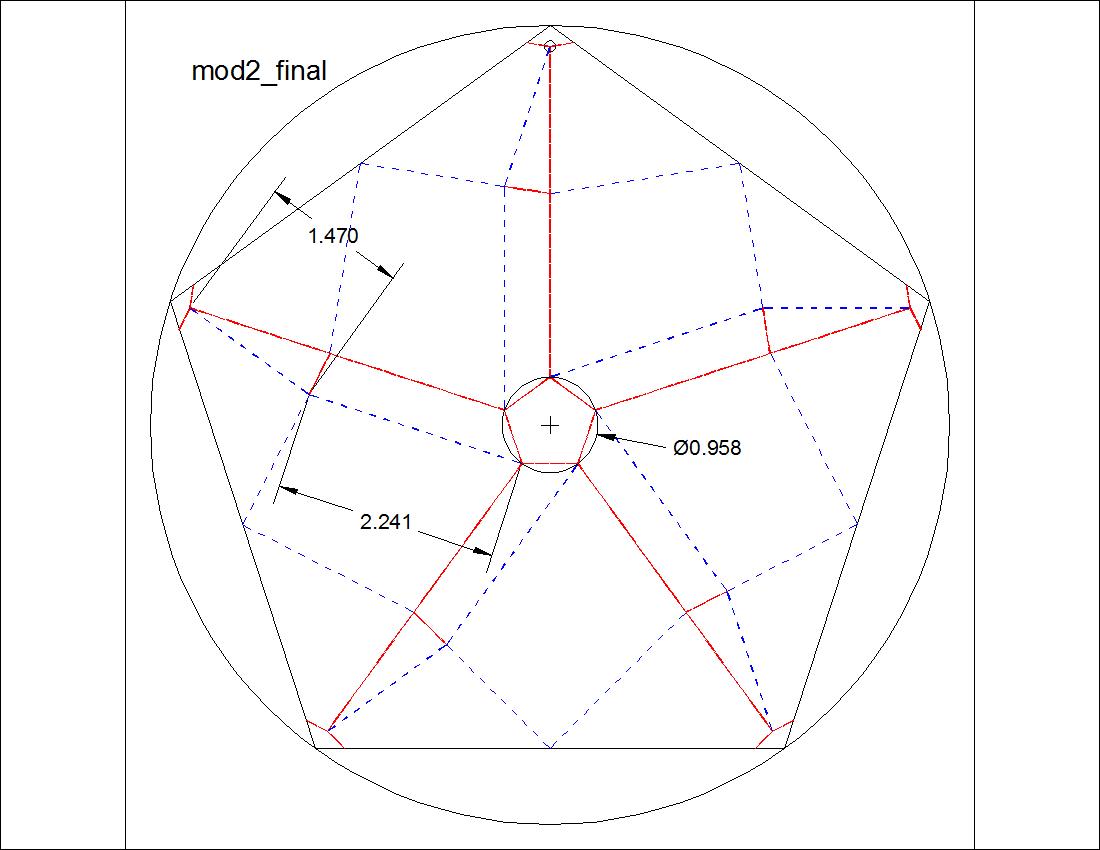


  The final diagram for Model-II is created by inserting this diagram on the separately

prepared five axis symmetric image drawing.

 For this exercise another pattern is printed on the back side. Notice that the pattern 

on the back side is the mirror image of the same pattern with respect to the horizontal axis

through the center.

Fig. 3-11A Pattern Diagram - Front
click here to enlarge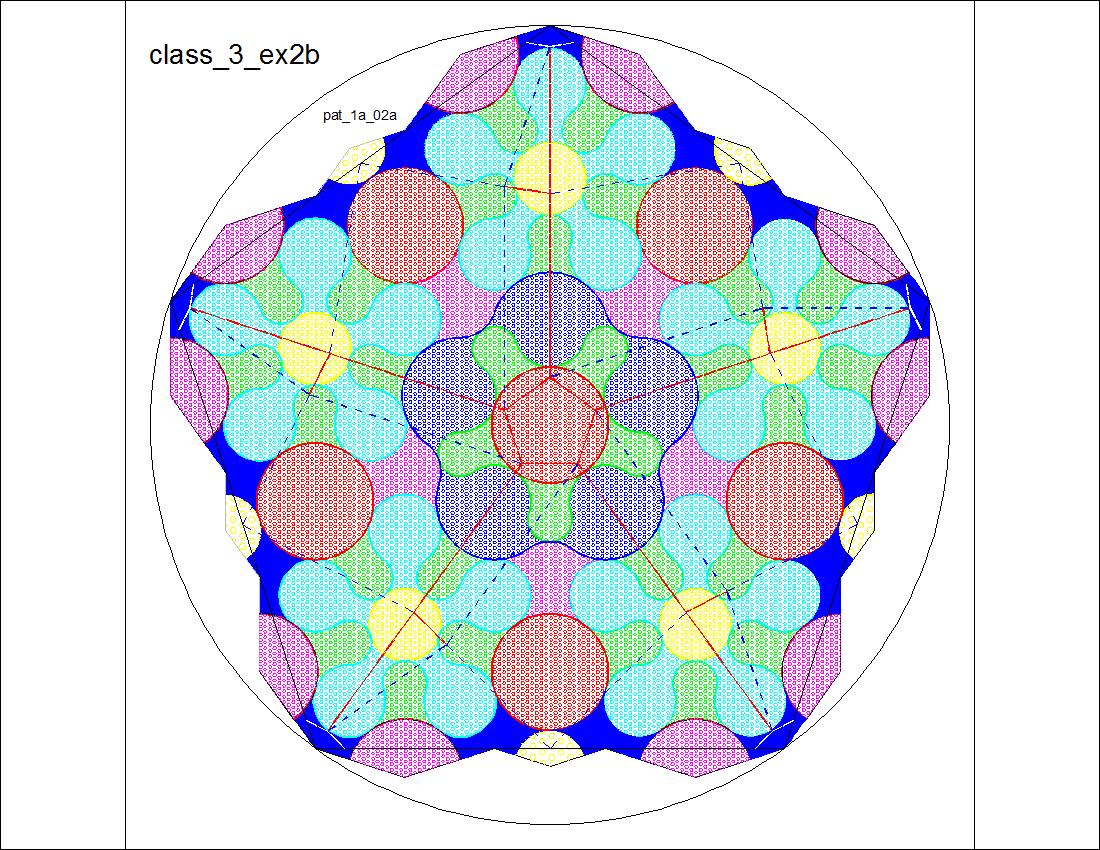

Fig. 3-11B Pattern Diagram - Back
click here to enlarge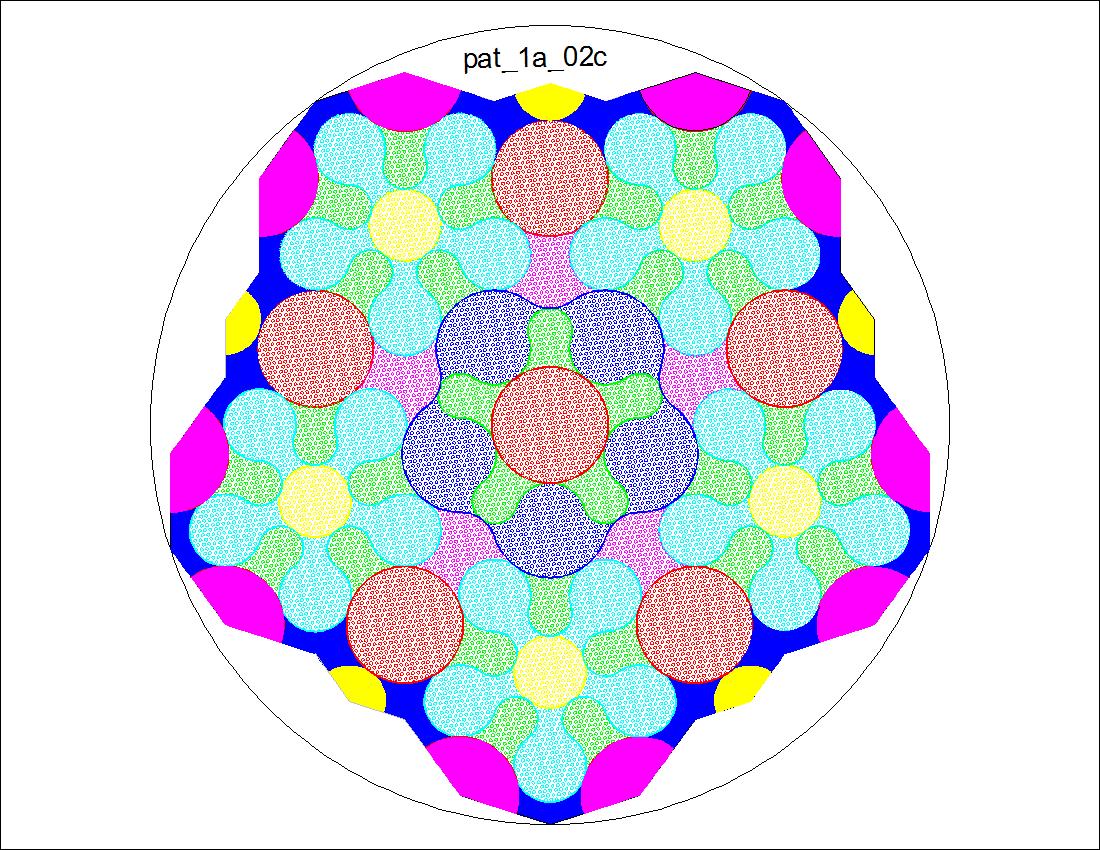

References

Montroll, John.: Galaxy of Origami Stars,ISBN-10:1480103047,John Montroll , 2012 .
Project F.: Origami - Nejiri Ori (in Japanese). Seibundo-Shinkosha,Tokyo,ISBN978-4-416-31200-1,2012 .
Note: Project F: group of three persons-Satoko Saito, Taiko Niwa, Tomoko Fuse