Go back to   Polygonal string

Tape Weaving - Rings of regular polygons using "Quilling Tape"

  The author has shown in  "Polygonal string" that rings of regular polygons
 can be created by folding a strip of paper with constant width. These tapes  are
 marked with crease lines which are drawn drawn manually or automatically by printer.
  The advantage of this approach is that it is possible to control the pattern
 of the final work, but as the number of the sides increases, it get more and more
 difficult to create the corresponding strip pattern.
 One of the difficulties is preparing the constant width paper tape.
 Then the authothe author came up with the idea of using Paper Tapes used in Quilling,
 and was awarded with surpringly pleasing results. 
 The following is a brief summary of the efforts so far.

Description of the procedure - Pentagon as an example

Let us begin with the simplest example (pentagon).

Preparation Stage

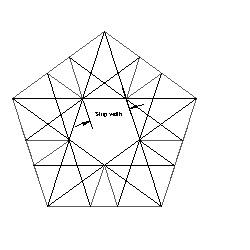
Step 1: Choose a paper strip size and print out a figure of pentagon for the selected
     paper width. Or it can be drawn on a piece of paper with compass and ruler. Unless  
     you cut out paper strips by yourself, many sizes of Quilling paper are available.  
     Quilling supply stores offer the sizes raging from 1/8 up to 1 inch,  but the  
     author thinks 1/8 is too small to handle. The author thinks that the sizes ranging
     from 3/8 to one inch are good choices. 
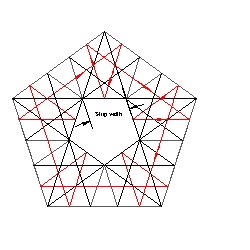
     The left figure below shows the basic folding patterns and the right figure shows
     the direction of the folding process by red arrows.

Pentagon Template          click here to enlarge

Folding direction          click here to enlarge

Step 2: Paste the paper onto a thicker piece of paper with weight index of more than 
       50 lbs.
   Note: most of the printer paper's weight index is 20 lbs (or 75 gram/mm2) in metric)
   If you have a direct paper feeding type printer (like Epson 1400), it is possible 
   to print out directly using paper up to 100 lbs index value.

Step 3: Begin laying a tape along the reference lines on the template sheet. 
       There are two methods to proceed.
       The first approach is suited for quilling paper, and the second ,
       for general cases like any adhesive tape, masking tape and any tape in general 
       including even fabric tapes.

Folding Stage

The First Method
     In the example of the first approach  the paper width is 3/4 inch.
     The length of tape required to go around the pentagon is approximately 23 inches.
     The length of the quilling tape prepared is 24 inches , so one tape is enough to   
     complete the job. Special attention must be paid during steps between "start" and    
     "step 1", also between "step 2" and "step3". The tape is returned between the tape  
     and the template sheet (not the back side of the template sheet).
     When the tape reaches the starting location, cut the tape and insert the endpoint 
     under the tape.
     If done correctly, the front and back look like the pictures shown. 
     Otherwise there must be some errors during the folding process.

Template    click here to enlarge	Start    click here to enlarge	Step 1    click here to enlarge	Step 2    click here to enlarge
Step 3     click here to enlarge	Completed (front view)     click here to enlarge	Rear View     click here to enlarge

The Second Method
For this case , the paper width selected is 3/8 inch.
Comparing the pictures of step 2, the readers can see the difference between the two methods.
Instead of going between tape and template sheet, the tape goes along the back of the template sheet.
As a result, an uncovered area of pentagon shape (see step 3 fiure below) remains.
And when the tape reaches the starting point, two uncovered areas are left in the front.
Situation is the same for the rear view.(see "End of 1-st cycle" figures)
In order to cover these blank space, one more cycle is required.
So this method requires exactly two times of tape length.
But this method gives exactly the same pattern on both sides of the sheet.

Step 2    click here to enlarge	Step 3    click here to enlarge	End of 1-st cycle(front)    click here to enlarge
End of 1-st cycle(back)    click here to enlarge	Complete (front)    click here to enlarge	Complete (back)    click here to enlarge

The Modified second method

    In order to save this extra waste of tape, 4 blank areas (two each on front and back)
   as shown in figures above must be covered before the folding starts. This is shown in
   the following figures. It is interesting to note that in general
     this type of modification can be applied  to any odd numbered polygons.
 

Method 2 - modified    click here to enlarge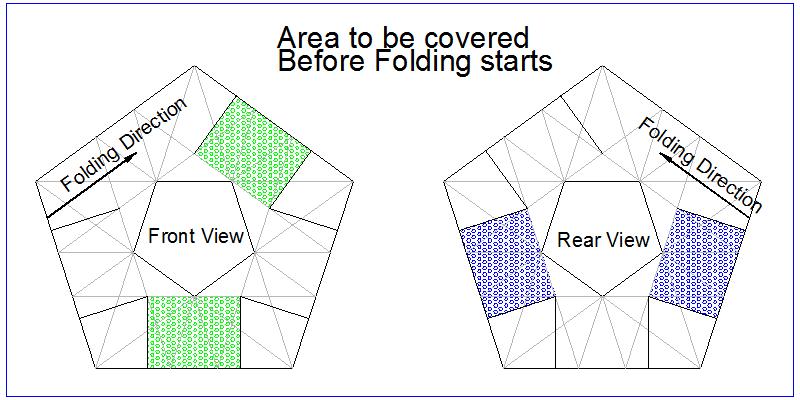

Go back to   Polygonal string