全ての曲線は多数の円で構成される - 縮閉線(Evolute)
ここでの主旨は、どの曲線も多数の真の円から作られるというこである。
（記：真直ぐな線分は無限長の半径を持つ円として解釈される。）
簡単な図面を見てみる：
***********************************curve_sample_1.dwg ***********************************
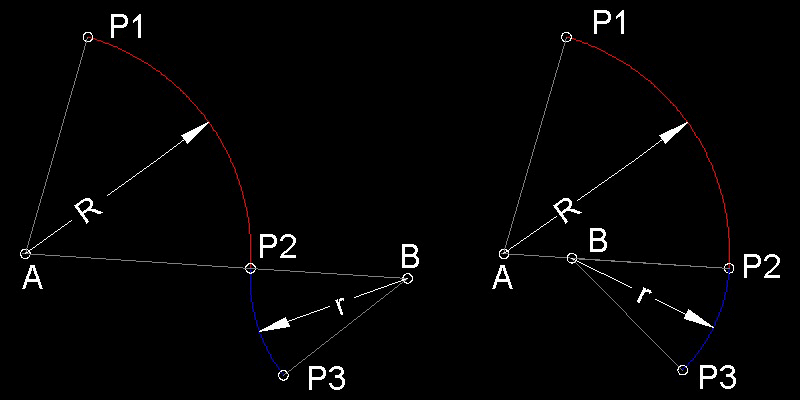
両曲線は半径 R の弧 A-P1-P2 と半径 r の弧 B-P2-P3 から構成される。
これら両曲線の違いは、二番目の弧の中心（点 B）の位置である。
半径が変わる点（点P2）と２つの弧の中心（点 A と点 B）は同一線上にあることに注目する。
このことが点P2 での傾き（または接線）の
連続性を保証する。複数の弧によって滑らかで連続な曲線を描くには、次のルールを適用する：
"半径が変わる点においては、新しい半径の中心は、その点と前の弧の中心とを結ぶ線上になければならない。"
この例では、最初の弧が半径 R から r に縮小する端点P2 にくる時、弧の中心は前の弧の中心"A" と点P2 とを結ぶ線に沿って点"B"へ移動し、
新しい弧がそこから始まる。このようにすることで、点P2 での傾斜、即ち両方の弧に共通な接線は連続となり、滑らかな曲線が保証される。
これを証明する簡単な図をもう一つここに示す。
***************************************ying_yang.dwg ***************************************
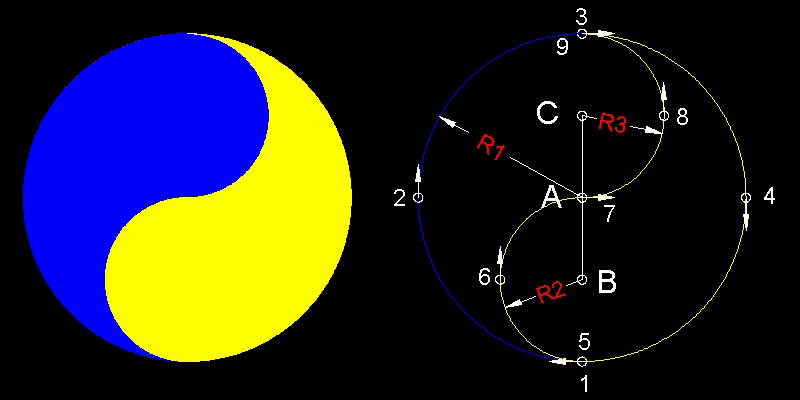
図中での番号は弧の移動順を表す。一番最初の弧の中心の変化は、弧が点"5"に到達する時に生じる。
この変化は "A" と "5" を結ぶ線沿いである。同様に、点"7"での中心の移動は、"B" と"7" を繋ぐ延長線上で発生する。
この図面とアニメーションの作成方法：
プログラム ying_yang.lsp を (load "ying_yang") でロードする。
コマンド ラインから ying_yang と実行命令をタイプする。
上の２つの例では、曲率の中心(= 円)は線分に沿って移動するが、一般に曲線が複雑であると（例えば卵の形のように）、
円の中心は曲線に沿って移動する。
この曲線を 縮閉線 (Evolute) という。
定義： 曲線の縮閉線は曲率中心の軌跡である。
縮閉線(Evolute)を使って楕円の近似形を描いてみよう。
ここでの最終目的は、実際の卵の形を幾つかの弧を使って描くことである。鶏卵の形に一番似ている解析曲線は楕円である。
その違いは一般に、鶏卵の形では上端の半径が下端より小さくて２つの異なる半径を持っていることである。
そこでまず最初に簡単な楕円を幾つかの弧を使って描くことを考えてみよう。
そしてその後で同じ方法を実際の卵の形を描く一般的な方法に拡張して行こう。
先ず縮閉線 (Evolute) の概念を使って楕円を描いてみよう。
ステップ 1: 楕円に関する縮閉線を定義する
楕円は次の式で定義される (x/a)2 + (y/b)2 = 1 , ( a > b とする)この楕円の縮閉線は[2, 3]によれば (x/A)2/3 + (y/B)2/3 = 1 ここで Aa = Bb = a2 - b2 最小半径(r) = b2/a(下の図でその中心を赤色で示す） 最大半径(R) = a2/b(下の図でその中心を黄色で示す）
２つの楕円に関する縮閉曲線を次に示す。 これらの楕円は X-軸 に関して対称であるから、上半分の縮閉線だけを考えることにする。
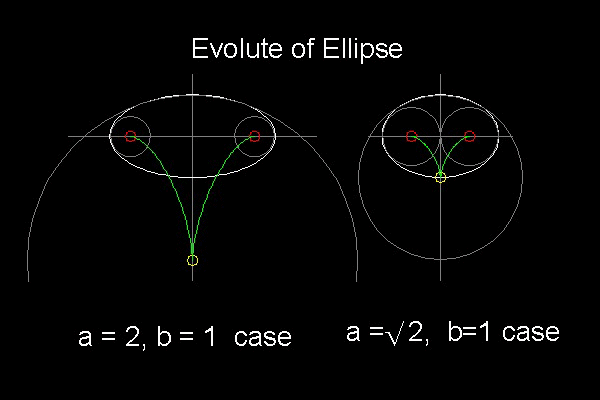
この図面の作成方法：
プログラム evolute.lsp を (load "evolute") でロードする。
コマンド ラインから draw_ellipse_evolute と実行命令をタイプする。
楕円の線を選ぶと 緑色の線で 縮閉線(Evolute curve) が描かれる。
一つの縮閉線を作ったら左へ移動して次を作る。
これらの図面を見ると楕円は大まかに大小二つの弧と、
これらをつなぐもう一つの弧で描けるのではないかと予想される。
問題はその "つないでいる" 弧をどのように見つけるかである。
"つないでいる" 弧を定義するために "根軸 (Radical Axis)"
の考えが使われる。
**********************ellipse_evolute_2.dwg **********************
ステップ 2: 根軸(Radial Axis): (a) 求め方
次の説明は一般にどの二つの円にも当てはまるが、ここでは楕円を取り扱っているので、円C1(= C ) は半径が b2/a の最小半径円で、
円C2(= C' ) は半径が a2/b の最大半径円であると考えることにする。
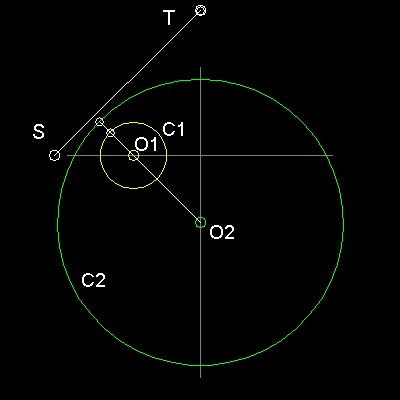
解析的に： 円 C : C (x,y) = x2+y2+ 2gx+ 2fy+c = 0 円 C': C'(x,y) = x2+y2+2g'x+2f'y+c'= 0 よって C(x,y) - C'(x,y) = 0 (1)これらを図中では点 S (X0, 0) と点 T (0, Y0) で示す。
は、円C と C' の"根軸"(Radical Axis)と呼ばれ、 線分の方程式は： 2(g - g')x + 2(f - f')y + c - c' = 0 または x/ Xo + y/Yo = 1 となる。 この線が X軸 及び Y軸 と 交差するの点の座標は Xo = -(1/2)(c-c')/(g-g') Yo = -(1/2)(c-c')/(f-f') となる。
線分ST は (1)式 を満たす点の軌跡で、
その線上のどの点からでも両円への接点までの距離は同じ！！
************radical_axis_1.dwg ************
2つの円の点S と点T を求める：
プログラム evolute.lsp を (load "evolute") でロードする。
コマンド ラインから radical_axis と実行命令をタイプし 2つの円を選択する。
このコマンドは図中の線分ST を描く。
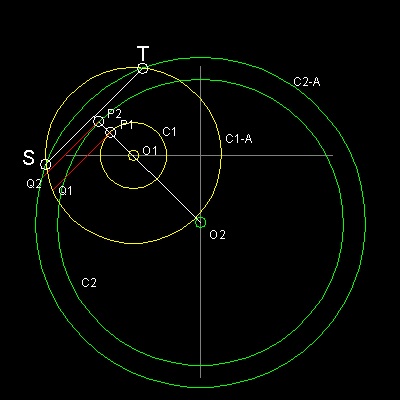グラフィックで：
これらの点で線分O1O2 に垂直である。 中心が O1 で半径が O1Q1 の円 C1-A を描く。
同様に、中心が O2 で半径が O2Q2 の円 C2-A を描く。 これら２つの円の交差する点は S と T である。
線分ST は、円C1 と C2 の 根軸 (radical axis) である。
************radical_axis_2.dwg ************
ステップ 3: 根軸: (b) 求め方
"根軸"の重要な特性：1. 線分ST は線分O1O2 に垂直である。
2. 線分ST 上のある一点から引いた接線の長さは、円C1 と C2に関して同じである。
この最後の特性は、円C1とC2間のギャップを埋めるため、縮閉線とそれに関連した円を求めるのに用いることができる。
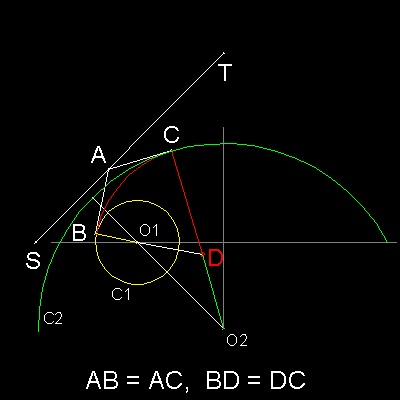左の図では、A は線分ST 上の点である。
B, C はA から円C1 とC2 に引いた接線の端点である。
点C と O2 を結ぶ。
線分CO2 とBO1 の延長線が交わる点が D。
ST は根軸なので、AB = AC、
両方の角 ABD と ACD は90度で、 BD = CD である。
よって、O1 と O2 の間で点D が縮閉線として選択されると、
３つの弧からなる連続した滑らかな曲線が得られる。
第一の弧: O1 が中心, x-軸からスタートし点B へ
第二の弧: D が中心, B からスタートし C で終わる
第三の弧: O2 が中心, C からスタートしY-軸に関して点Cと対称なる点へ
************radical_axis_3.dwg ************
５つの円を用いて楕円を描く方法
E.H.Lockwood は、楕円がコンパスと定規で描けることを示した。[3, 4]
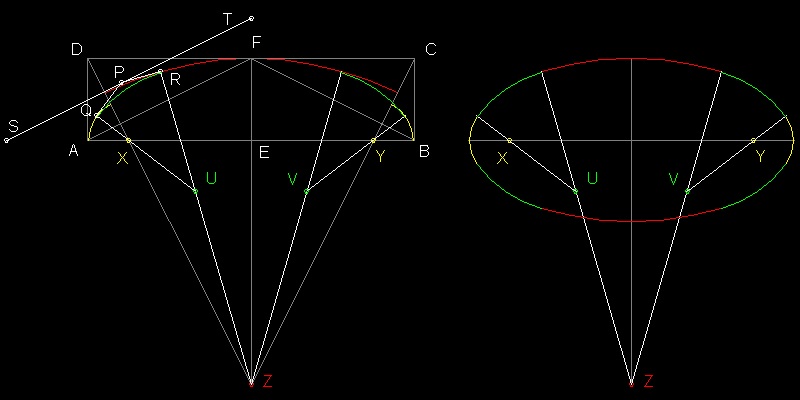
************************************ellipse_Lock_01.dwg ************************************
５つの円を用いて楕円を描く方法
- AB = 2a, BC = AD = EF = b の長方形を描く
- 点D から線分AF に垂直な線を引く。それが線分AB と X で交差し、線分EF と Z で交差する。
右側も同じようにし、その交点を"Y"とする。 - 中心がX で半径AX の弧を"A"から始めて線分XDまで描く(黄色)。
同様に点Y にも行う。
半径AXは、点 "A" での最小半径 (b2/a)に等しい。
その理由--三角形ADX と EAF は相似である、故に(AD/AX) = (AE/EF) つまり b/AX = a/b - 中心が"Z" で半径FZ の弧を線分DZから始めて線分CZまで描く(赤色)。
半径FZは、点"F" での最大半径( a2/b) に等しい。
その理由--三角形DFZ と FEA は相似、故に(DF/FZ) = (FE/EA) つまり a/FZ = b/a - 上記の方法の一つを使って"根軸" (線分ST)を引く。その線上に点P を指定し、
２つの円に接線を引き、その端点を P と Q とする。
更に QX を延長し線分RZ との交点U を求める。同様の操作を右側にも行って点V を求める。" これら５つの点 X,U,Z,V,Y は近似曲線を作る縮閉線である。"