Doubling the Cube
Go to   Fun_Math Content Table   Three Famous Problems   Delian Problem

Doubling the cube by Greek Mathematicians

Archytas- 3D solids intersection solution

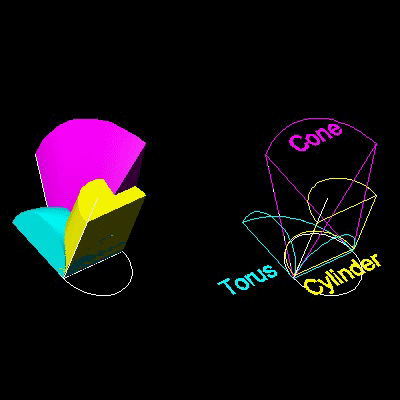
The first solution was given by Archytas of Tarentum (circa 428 BC-350 BC) .
The remarkable thing about this fact is his solution is the intersection of three surfaces of revolution,when most of his contemporary mathematicians were dealing only with the 2D , plane geometry.
In historical perspective, he lived long before Euclid of Alexandria (circa 325 BC-265 BC) wrote his famous book "The Elements".
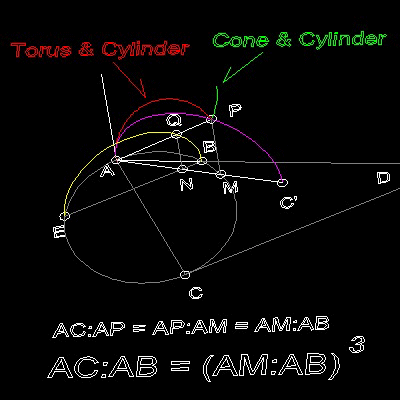
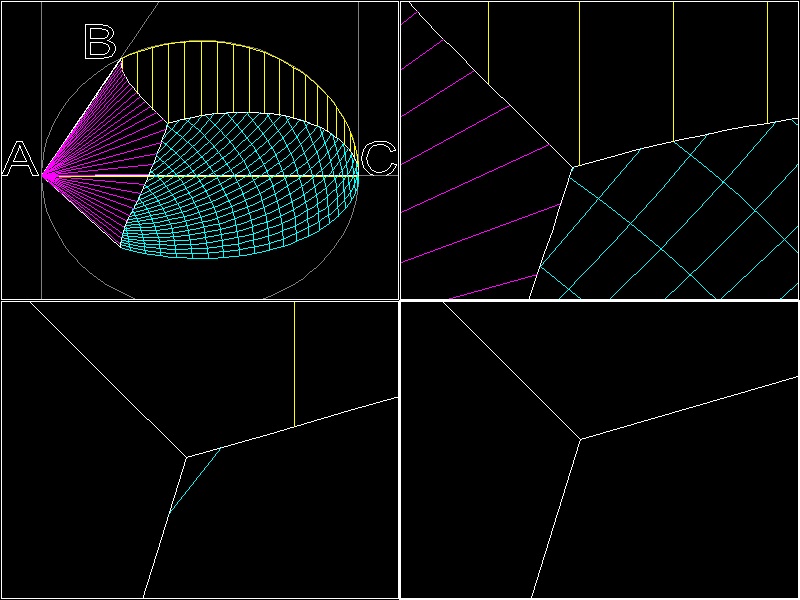
In the drawing below, the objective is to find length (AC/AB)1/3 for given lengths of AB & AC.

These are the steps to find such line.
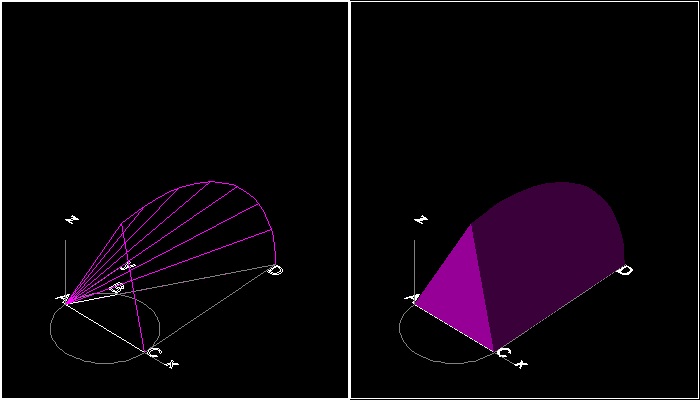
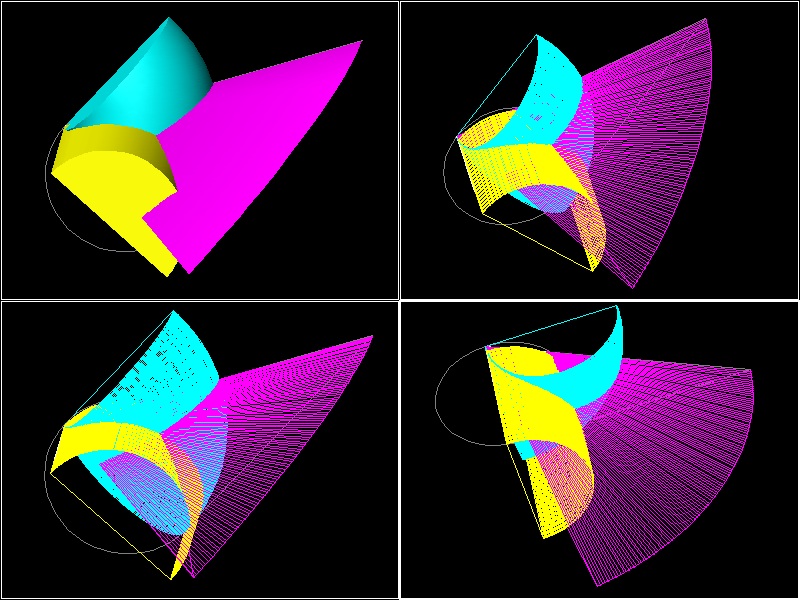
(1) Three surfaces of revolution meets at point P.
(2) Draw a line PM perpendicular to plane ABC.
(3) Point M will be on the circle ABC.
(4) Then AC/AP = AP/AM = AM/AB
(5) Therefore AC/AB = (AM/AB)3
if AB = 1, and AC = 2, then AM = (2)1/3

For the geometrical arguments regarding statements (3) & (4),refer to the ref.1 by Heath,
Here let us use analytical geometry to derive this.
Analytically three surfaces of revolution can be written as follows:
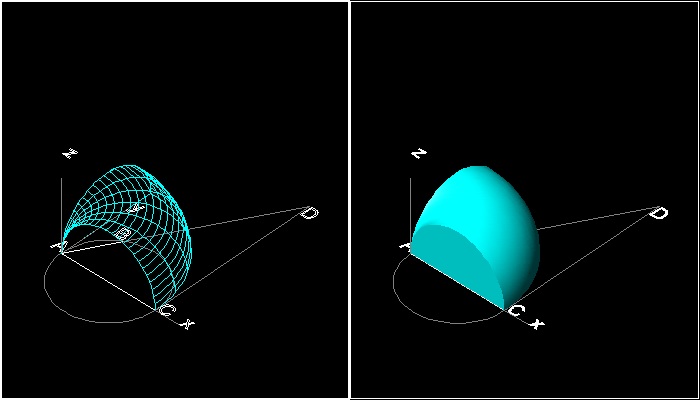
(1) the right cone :  x2 + y2 + z2 = (a/b)2x2
(2) the cylinder :     x2 + y2 = a x
(3) the torus :         x2 + y2 + z2 = a {x2 + y2}1/2
Combining (1) & (2), we have   x2 + y2 + z2 = {x2 + y2}2 / b2
From this and (3), we obtain
                a / {x2 + y2 + z2}1/2 = {x2 + y2 + z2}1/2 / {x2 + y2}1/2 = {x2 + y2}1/2 / b

or,         AC / AP = AP / AM = AM / AB


********* Archytas_Delian_model.dwg ********* ******** Archytas_Delian_result.dwg ********
To create this drawing :
   Load Archytas_Delian.lsp    (load "Archytas_Delian")
  Then from command line, type Archytas_delian_model for the left
  Similarly from command line, type Archytas_delian for the right.

Numerical Check of the result
Let us check the numerical value of line length AM,which is {x2 + y2}1/2.
Substituting (2) into (3), we obtain
                                                x2 + y2 + z2 = a ( a x )1/2                             ------------------------- (4)
Equating the right hand side of (1) and (4), x can now be determined as    x = {b4/ a }1/3 ---------- (5)
Substituting (5) into the right hand side of (2), we obtain
            x2 + y2 = a x = {a2 b4}1/3
Therefore, AM = {x2 + y2}1/2 = {ab2}1/3
The value for y & z can also be computed from the following result.
                                     y2 = {a2 b4}1/3 - {b8 / a2}1/3
                                     z2 = {a4 b2}1/3 - {a2 b4}1/3
If we let a = AC = 2, and b = AB = 1, then
AM = (2)1/3 and AP = (4)1/3
and x = (1/2)1/3 ; y2 = (4)1/3 - (1/4)1/3 ; z2 = (16)1/3 - (4)1/3
or, x = 0.7937005 , y = 0.9784889 , z = 0.9656298 , which is the 3-D coordinate value of the point "P".

Cylinder

A semi circle ABC is extruded in the z-direction (i.e,normal to plane ABC)
the equation for this cylinder:  x2 + y2 = a x

****************************** half_cylinder.dwg ******************************
To create this drawing :
   Load Archytas_Delian.lsp    (load "Archytas_Delian")
  Then from command line, type cylinder_2views

Torus

Rotate a semi circle ABC 90 degrees around the x-axis
The resulting semicircle is vertical to ABC plane. Rotate this semi-circle around z-axis 90 degrees.
The result is a quarter of a torus with zero inner diameter.
the equation for this torus:  x2 + y2 + z2 = a {x2 + y2}1/2

****************************** torus_90_deg.dwg ******************************
To create this drawing :
   Load Archytas_Delian.lsp    (load "Archytas_Delian")
  Then from command line, type torus_2views

Cone

Rotate AD around line AC (x-axis) 90 degrees.
This will create a quarter of a cone.
the equation for this cone:  x2 + y2 + z2 = (a/b)2x2
.
****************************** cone_90_deg.dwg ******************************
To create this drawing :
   Load Archytas_Delian.lsp    (load "Archytas_Delian")
  Then from command line, type cone_2views

More on intersections of three surfaces

Sometimes it is easier to see the intersecting boundaries if surfaces are displayed in 3D mesh . The following drawing is such a case where system varaibles ISOLINES are set to 400.
****************************** Archytas_3_surfaces.dwg ******************************
To create this drawing :
   Load Archytas_Delian.lsp    (load "Archytas_Delian")
  Then from command line, type draw_cone , draw_cylinder & draw_torus
Then split viewports into 4, using VPORT command. Change view point in each view port

More on intersections of three surfaces


****************************** intersection_3_surfaces.dwg ******************************
To create this drawing :
   Load Archytas_Delian.lsp    (load "Archytas_Delian")
  Then from command line, type draw_cone , draw_cylinder & draw_torus
Then use INTERSECT command to modify surfaces.
Split into 4 viewports, and change view directions.

How to locate point "P"

Start with the drawing intersection_3_surfaces.dwg. Zoom in to the point of intersection. Three view ports.
********************************* find_point_p.dwg *********************************

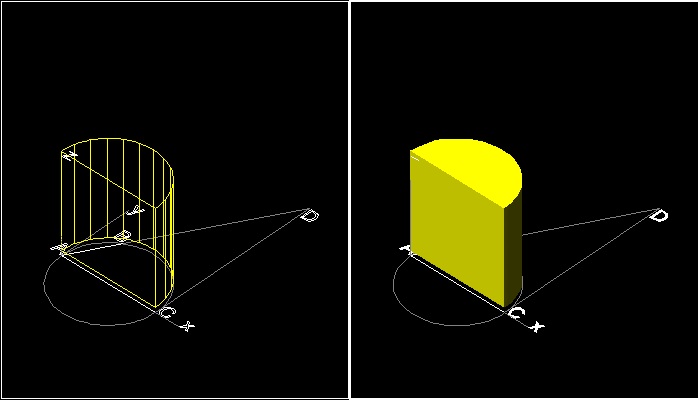
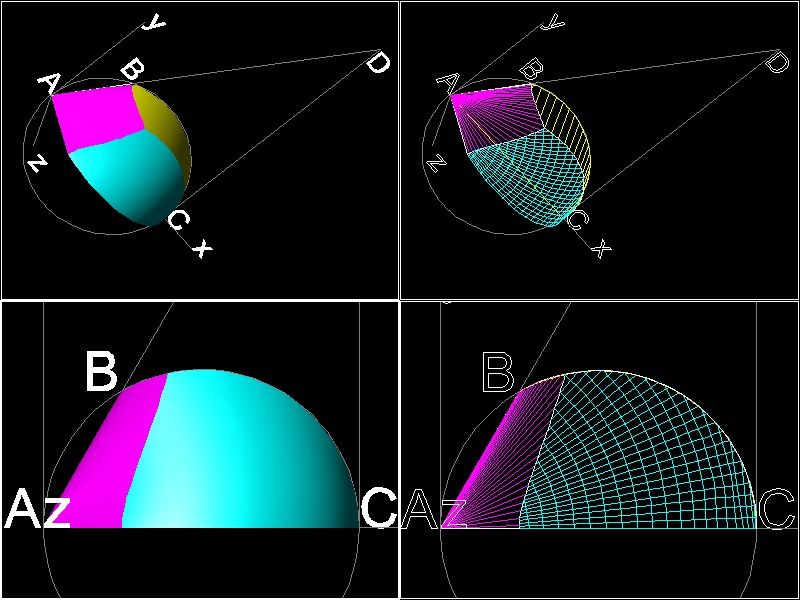
Explode the surface objects. Then the boundary lines become independent lines. Locate the point "P" using "END" osnap command.
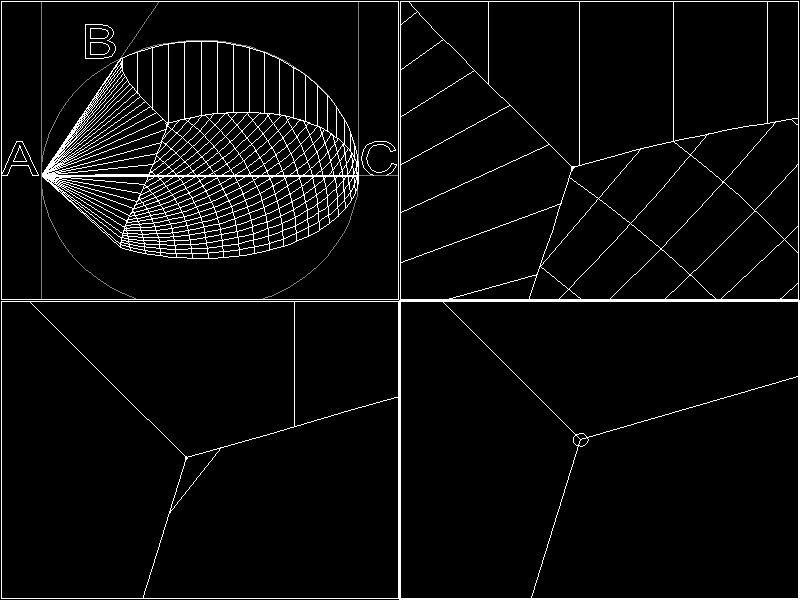
********************************* explode_find_point_p.dwg *********************************

Using LIST command, the following value will be displayed on the TEXT screen.
POINT Layer: "0"
Space: Model space
Handle = 663
at point, X=0.79370053 Y=0.97848890 Z=0.96562987
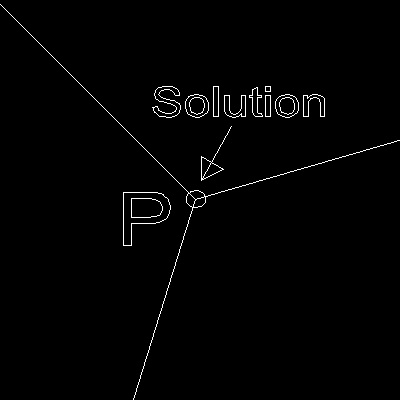
********** point_of_intersection.dwg **********

References

1. Heath, Sir L. Thomas:"A History of Greek Mathematics", VOL. 1, From Thales to Euclid., Dover.

Go to   Fun_Math Content Table   Three Famous Problems   Delian Problem

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved. .