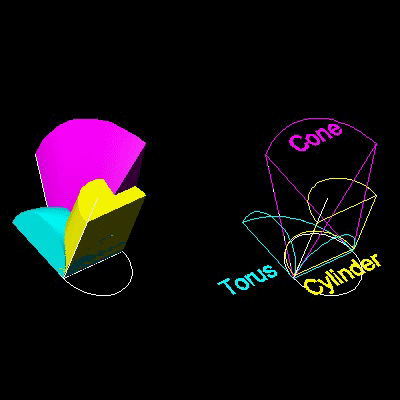
Archytas of Tarentum (circa 428 BC-350 BC)
discovered that a solution is finding the intersection of three surfaces of revolution.
The three surfaces of revolution used are
(1) the right cone : x2 + y2 + z2 = (a/b)2x2
(2) the cylinder : x2 + y2 = a x
(3) the torus : x2 + y2 + z2 = a {x2 + y2}1/2
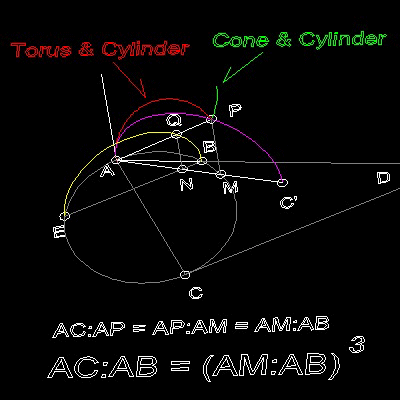
where AC = a, and AB = b
Then in the drawing, AC/AP = AP/AM = AM/AB.
This gives AC/AB = (AM/AB)3 and AM is the solution.
For detail, go to the section Archytas - 3D solids intersection solution.
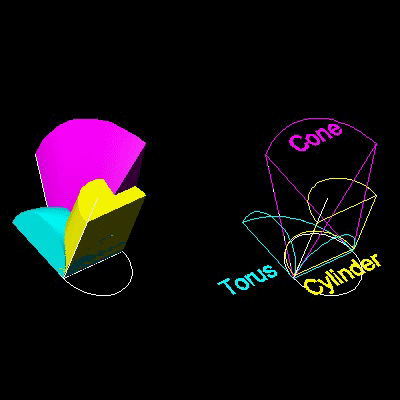
********* Archytas_Delian_model.dwg *********
******** Archytas_Delian_result.dwg ********
Eudoxus of Cnidus (408 BC - 355 BC) was a student of Archytas. He solved the problem by projecting the intersection of the cone and torus onto xy plane. The solution is the the point where such a curve crosses the circle ABC.
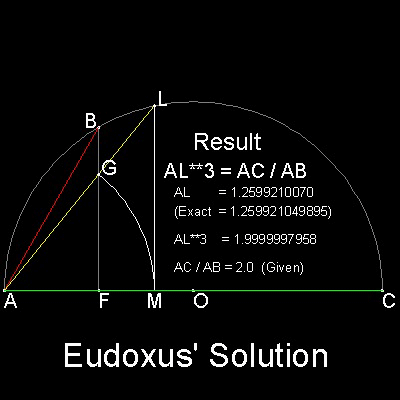
AB, and AC is the line segment between which two mean proportionals have to be found.
The steps go as follows:
1. Drop a line BF perpendiculat to AC.
2. Take any point G on BF, and with A as center and AG as radius, draw an arc cutting AC at M.
3. Erect a line normal to AC at M. This line intersects line AG at L.
4. When L is on the circle, then AL is the solution.
You can see the process in animation.
********** Eudoxus_Delian_desc.dwg *********
For detail, go to the section Eudoxus_Delian.
Menaechmus (circa 380 BC - 320 BC),
who is said to have discovered the conic sections, is also famous by his answer to Alexander the great.
"In geometry there is no royal road .".
He used parabolas and rectangular hyperbola to solve the Delian problem.
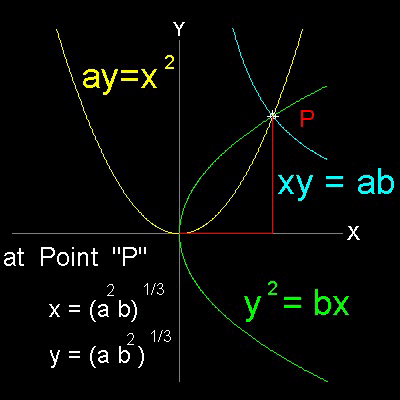
If x, y are two mean proportional between straight lines a, b, a / x = x / y = y / b then x2 = ay, y2 = bx , and xy = ab Therefore any two pair of these three curves, will give the solution to Delian problem. |
Animation to be added here.
******** Menaechmus_Delian_desc.dwg *******
For detail, go to the section Menaechmus_Delian.
Many historians agree that this solution is wrongly attributed to
Plato (427 BC - 347 BC) .
Generally accepted conclusion is that the solution was invented in the Plato's Academy by
someone contemporary with or later than Menaechmus .
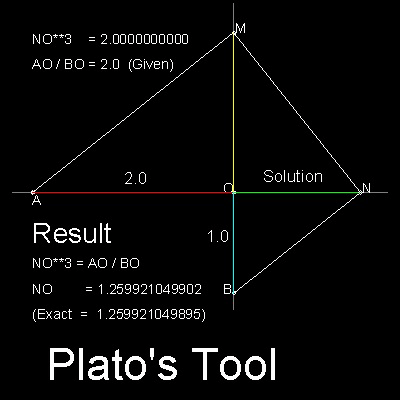
The basic concept is to find points M & N
on y and x -axis ,respectively
while keeping angle AMN and MNB
being equal to 90 degrees.
Then, 3 triangles AOM, MON, and NOB are similar.
Therefore, AO:OM = OM:ON = ON:BO
and ON3 = AO.BO2
*********** Plato_Delian_desc.dwg ***********
For detail, go to the section Plato_Delian.
Eratosthenes of Cyrene (276 BC - 194 BC) is also famous for estimating the size of the Earth.
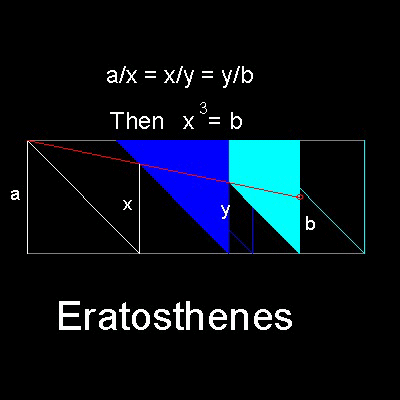
You can see the process in animation.
******** Eratosthenes_Delian_desc.dwg *******
For detail, go to the section Eratosthenes_Delian
Nicomedes (circa 280 BC - 210 BC) ,the inventor of Conchoid curve, used his own invention to solve Delian problem.
The length of AB and BC are given.
D , E are the bisectors of AB , BC ,respectively.
CG = AB, CF = AD, and GF is parallel to CZ.
Objective is to find length equal to: {AB.BC2}1/3 and {AB2.BC}1/3
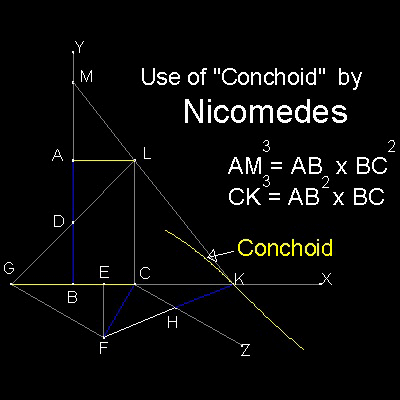
Result : AB / AM = AM / CK = CK / BC
Key : To find point K such that CF = HK
Conchoid is used F as "pole", CZ as "ruler",
and "distance" equal to CF(= AD).
You can see the process in animation.
********* Nicomedes_Delian_desc.dwg ********
For detail, go to the section Nicomedes_Delian
Philon of Byzantine (circa 280 BC - 220 BC) solved the "Delian"problem as follows:
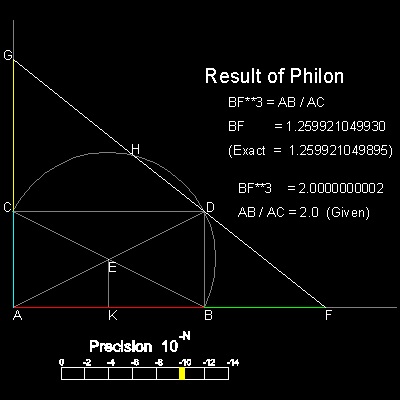
AB and AC are the two given straight lines.
draw a rectangle ABDC
point E is the intersection of diagonals,AD and BC.
draw a semi-circle BDC with diameter,BC .
from D ,draw a line.This intersects AB and AC at F and G, respectively.
This line also cuts the semi-circle at H.
When this line is chosen such that GH = DF,
Then, BF and CG are the solutions.
Note: Precision bar shows the value of |GH - DF| .
You can see the process in animation.
************ Philon_Delian_desc.dwg **********
For detail, go to the section Philon_Delian
The solution by Apollonius of Perga (circa 262 BC - 190 BC) is very similar to that of Philon.
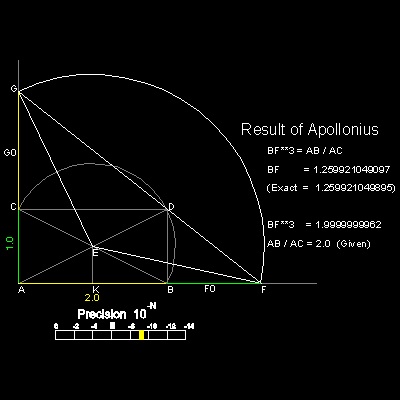
Again AB and AC are given straight lines,and semi-circle BDC is also drawn.
Draw a circle with center E, cutting the extended lines of AC & AB
at F and G, respectively.
Connect FD and DG.
When 3 points F,D, and G are colinear, CG & BF are solutions.
You can see the process in animation.
********** Apollonius_Delian_desc.dwg *********
For detail, go to the section Apollonius_Delian
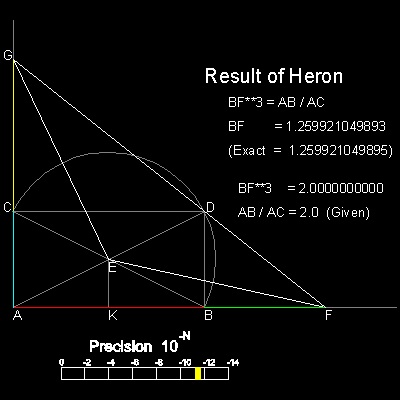
The Delian solution by
Heron of Alexandria (circa 10 AD - 75 AD)
is also very similar to that of Philon.
The difference is that a line passing through D is chosen
such that EF = EG
Then, CG and BF are the solutions.
You can see the process in animation.
*********** Heron_Delian_desc.dwg ***********
For detail, go to the section Heron_Delian
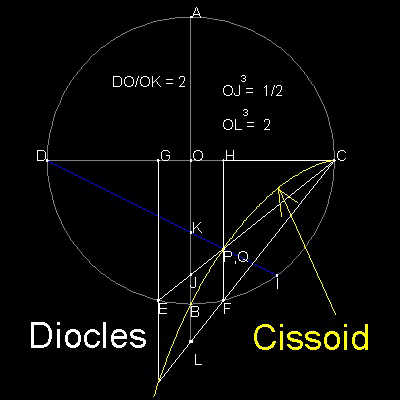
Diocles (circa 240 BC - 180 BC) invented Cissoid, and used this curve for Delian soultion.
*********** Diocles_Delian_desc.dwg **********
You can see the process in animation
For detail, go to the section Diocles_Delian
In his book , Pappus of Alexandria (circa 290 AD - 350 AD) described this method by some unknown person with criticism.
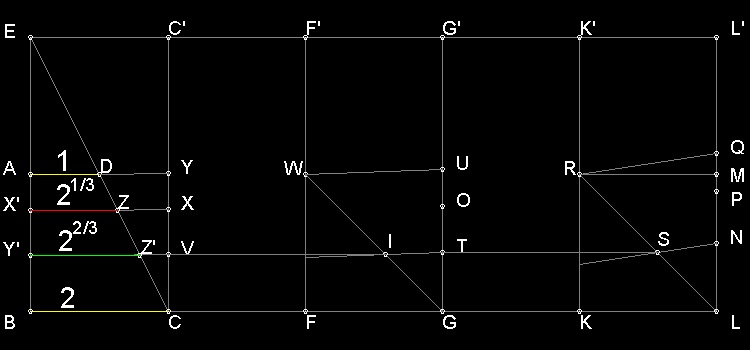
*************************** approximation_Delian_desc.dwg **************************
You can see the process in animation.
For detail, go to the section Approximation_Delian
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.