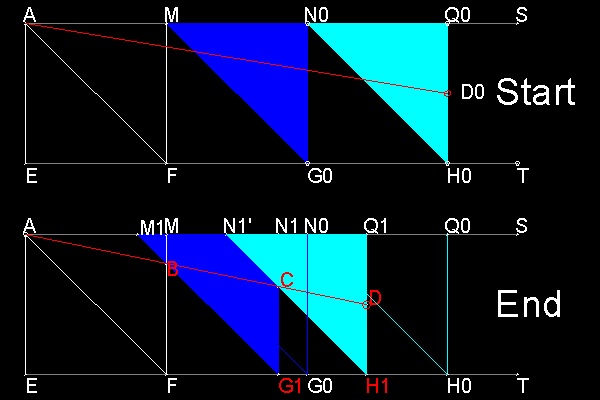
How the Delian tool invented by Eratosthenes works is illustrated below:
The tool is made up of two parallel horizontal bars (AS & ET),
two movable triangle plates( (NGM, QHN)
,and fixed trianlge AMF.
Two movable triangles slide along AS and ET.
The process to find cubic root is done as follows:
(1) Select a point "D" on line QH.
Let AE = a, and DH = b
(2) Move triangle NQH (cyan color) to the left, and draw a line AD.
(3) Move triangle MNG (blue color) to the left so that line MG comes to the
point of intersection between AD and MF.
(4) Check the distance between intersection of MG and AD, and
intersection of NH and AD.
(5) Repeat step (2) until the distance calculated in (4) becomes less than
a specified small number.
At the final stage ,
3 triangles ABF, BCG1,and CDH1 are similar.
Then BF /CG1 = CG1 / DH1 (1)
And 3 triangles AEF, BFG1, and CG1H1 are similar.
Then AE / BF = BF / CG1 (2)
Then,combining (1) and (2),
AE / BF = BF / CG1 = CG1 / DH1
Or, a / BF = BF / CG1 = CG1 / b (3)
Therefore, BF = {a2b}1/3 and CG1 = {ab2}1/3
For example, when a = 2, and b = 1,
BF = 41/3 and CG1 = 2 1/3
|

********** Eratosthenes_Delian_process.dwg *********
You can see the process in animation.
To create this drawing :
Load Eratosthenes.lsp (load "Eratosthenes")
Then from command line, type Eratosthenes
To create animation:
After executing "Eratosthenes" above, clear the screen by refresh_all command
Then (jpg_setup "test_file") to name jpg files.
After (setq jpg_yes 1), execute create_jpg from command line.

********** Eratosthenes_tool_run.dwg *********
To create this drawing and animation:
Load Eratosthenes.lsp (load "Eratosthenes")
Then from command line, type Eratosthenes
This drawing is the result of aborting the run by hitting ESC key.
Then add texts for explanation.
To be added in the future.
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.