Doubling the Cube
Go to   Fun_Math Content Table   Three Famous Problems   Delian Problem

Doubling the cube by Greek Mathematicians

Solution by Eudoxus

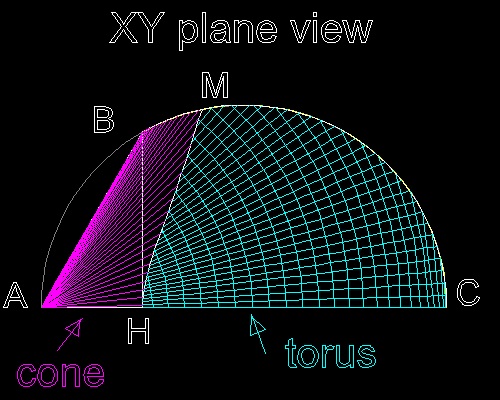
Eudoxus of Cnidus (408 BC - 355 BC) was a student of Archytas. He solved the problem by projecting the intersection of the cone and torus onto xy plane. The solution is the point where such a curve crosses the circle ABC.
Curved line between H and M is the line of intersection between cone and torus.
Arc BMC is the surface of cylinder intersecting cone (BM) and torus (MC).


********** Archytas_projection_on_xy.dwg *********

Curve used by Eudoxus

Erasing all generator lines in surfaces, the above drawing now looks like the one shown below.
The curve shown in magenta color is the boundary 3D double curvature line between cone and torus, which is projected down to xy plane.
Eudoxus found a way to draw this curve on xy plane.


********** Eudoxus_desc.dwg ********* 

 
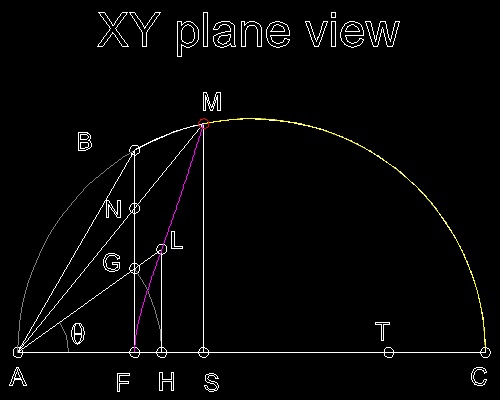
     In the drawing, AB = b and AC = b
Since BF is perpendicular to AC, BF2 = AF x FC.
Then     AB2 = AF2 + BF2 = AF2 + AF x FC = AF (AF + FC) = AF x AC 
or       AF = AB2/ AC = b2 / a
Then if angle GAF = q,  AG = AF /cos(q) = AF sec q = AH

And    AL = AH sec(q) = AG sec(q) = AF sec2q
If we express the location L in polar coordinate, 
using r as radius and angle q,
		r = (b2/a) sec2q					  (1)
Now  back to the surface equations for Cone and Torus. 
 the right cone : x2 + y2 + z2 = (a/b)2x2			  (2)

 the torus      :  x2 + y2 + z2 = a {x2 + y2}1/2		  (3)
Equating the right hand sides of (2) and (3), we obtain,

		x2 = (b2/a) {x2 + y2}1/2
Multiplying both sides by {x2 + y2}1/2, and using the relations
		r = {x2 + y2}1/2
		sec(q) = {x2 + y2}1/2 / x
Final result is 
		r = (b2/a) sec2q
which is exactly the same as (1).

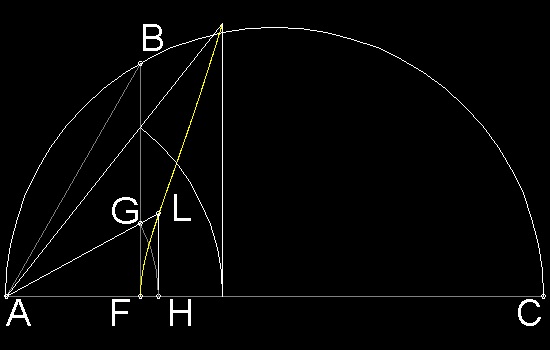
Therefore the curve given by (1) is the projection of the intersection 
between cone and torus onto plane ABC.

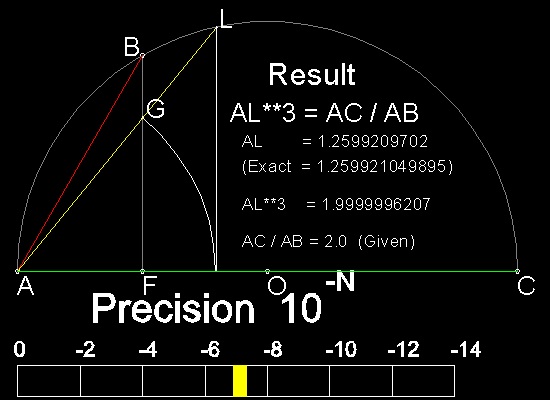
It is also  interesting to note that (AC/AB) times the length of AS (= AT ) is
equal to the length of AP in Archytas's solution.
	AM2 = AS2 + MS2 =  AS2 + AS x SC = AS (AS + SC) = AS x AC
So	AC x AS = AM2 = AB x AP
Therefore	AP = (AC/AB) x AS 
When AB = 1, and AC = 2, AP = 2xAS = AT

Drawing Eudoxus curve

In the days of Eudoxus, trigonometry has not been developed yet, so the curve was drawn in the following way.
1. Drop a line BF perpendiculat to AC.
2. Take any point G on BF, and with A as center and AG as radius, draw an arc cutting AC at H.
3. Erect a line normal to AC at H. This line intersects line AG at L.
4. Curve will be generated by connecting these point L.


********************* Eudoxus_curve.dwg *********************

You can see the process in animation .

To create this drawing and animation:
   Load Eudoxus.lsp    (load "Eudoxus")
  Then from command line, type draw_Eudoxus_curve
To see how to draw the curve, try test_1 & test_2.

Find the solution by repetitive zooming

In order to find the point of intersection, repetitive zooming is required.


***************** Eudoxus_Delian_result.dwg ******************

You can see the process in animation .

To create this drawing and animation:
   Load Eudoxus.lsp    (load "Eudoxus")
  Then from command line, type Eudoxus_Delian

References

  1. Heath,Thomas L. :"History of Greek Mathematics Vol. I From Thales to Euclid" Dover 1981
Go to   Fun_Math Content Table   Three Famous Problems   Delian Problem

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved. .