Doubling the Cube
Go to   Fun_Math Content Table   Three Famous Problems   Delian Problem

Doubling the cube by Greek Mathematicians

Plato's Cube doubling Tool

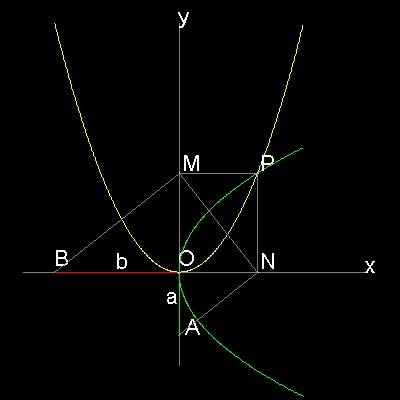
The basic concept of Menaechmus's method is to rotate three similar right triangles around one point "O" clockwise starting from BO.(See the #3 case of Menaechmus below).

There are multiple ways to accomplish this motion by mechanical constructions.

One way is as follows:
ANM is a rigid bar with angle ANM set to 90 degrees.
Bar BM moves in such a way that it always stays perpendicular to MN.
Restrictions: BM passes through point B, and AN passes through point A.

********** Menaechmus_Delian_3.dwg *********

A sample is shown in the next figure.



********** Plato_Delian_tool.dwg *********

A (Japanese) carpenter's square is used as a rigid 90 degrees tool, and a drafting triangle is used to slide along this square.
For reference, exact solutions are
ON = (2)1/3 = 1.2599.. , and OM = (2)2/3 = 1.5874..
In the figure, ON =1.25, and OM = 1.55 ~ 1.6

Plato's Delian Solution



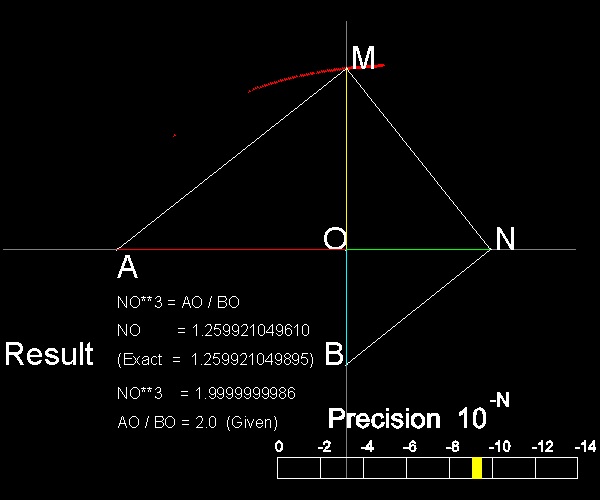
********** Plato_Delian_result.dwg *********

You can see the process in animation

To create this drawing and animation:
   Load Plato.lsp    (load "Plato")
  Then from command line, type Plato_Delian

Curve of the point M

The graphical soution above also plots point "M" in red color. The process continues until the point comes closer within the pre-specified criteria of convergence(1.e - 9).
Let us find out what kind of curve these points lie on.



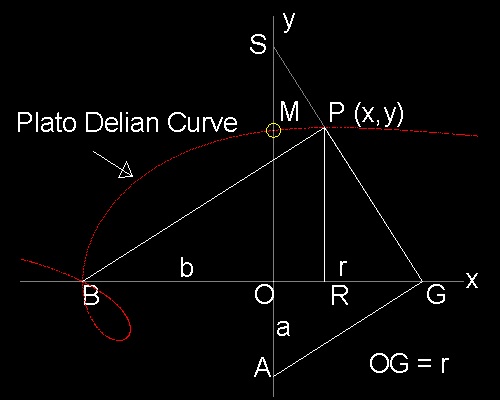
********** Plato_Delian_curve.dwg ********* 

 
 BPGA is the Plato's apparatus. G is on x-axis, but P is not on y-axis.
 PR is drawn perpendicular to x-axis, and extend GP to meet y-axis at S.
 	
 In the drawing, AO = a, BO = b, PR = y, OR = x, and OG = r

 In the right trianlge BGP,
	BR.RG = PR2
or	(b+x)(r-x) = y2                         (1)

 Since trianlgle SOG and PRG are similar,
	PR:RG = SO:OG = OG:OA
or	y/(r-x) = r /a					   (2)
 Eliminating r from (1) & (2),
 we obtain,as the locus of point P (x,y), the following equation of curve.

	a(b+x)2 = y(x2 + y2 + bx)  (3)

This is a curve of cubic terms in y, and shown in red dot in the drawing.
A very interesting shape !
 
 The solution point (M) is the intersection of this curve and y-axis.
 It is given by letting x = 0.
 Therefore 
	y3 = OM3 = ab2

Note here that if we choose line BPG as a rigid frame and try to find point G 
,then the equation will be obtained by changing a to b, x to y in (3) .
        b(a+y)2 = x(x2 + y2 + ay)

The intersection is obtained by letting y = 0.
or 	ba2 = x3 = ON3

To create this drawing :
   Load Plato.lsp    (load "Plato")
  Then from command line, type test_2 for plotting red points.

Go to   Fun_Math Content Table   Three Famous Problems   Delian Problem

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved. .