 Dinostratus (about 390 BC- about 320 BC),
a brother of Menaechmus (about 380 BC - about 320 BC),
gave a proof for the following proposition using
"reductio ad absurdum".
Dinostratus (about 390 BC- about 320 BC),
a brother of Menaechmus (about 380 BC - about 320 BC),
gave a proof for the following proposition using
"reductio ad absurdum".
 Dinostratus (about 390 BC- about 320 BC),
a brother of Menaechmus (about 380 BC - about 320 BC),
gave a proof for the following proposition using
"reductio ad absurdum".
Dinostratus (about 390 BC- about 320 BC),
a brother of Menaechmus (about 380 BC - about 320 BC),
gave a proof for the following proposition using
"reductio ad absurdum".
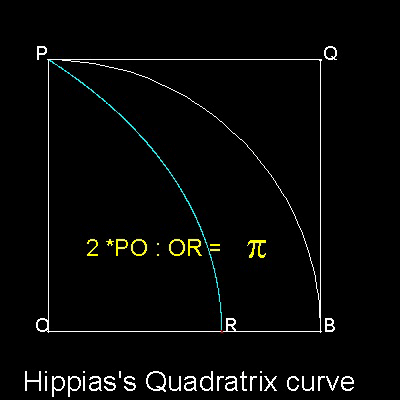
(arc PB) : PO = PO : OR
Or OR = (2/p) PO
For detail of the proof, see ref.1.
The modern derivation of this relation is given in the next section .
******* Hippias_circle_squarer_desc.dwg *******
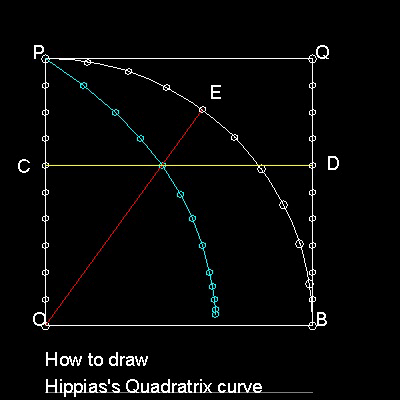 OBQP is a square.
OBQP is a square.
Divide both OP and BQ in equal parts N.
Divide a quarter circle BP into the same number N. Point C,D & E arer such points.
Horizontal line CD(yellow) and polar line OE(red) intersect .
The locus of such points(cyan color) is the "Quadratrix".
You can see the process in animation.
*********** quadratrix_curve_10_div.dwg ***********
To create this drawing and animation:
Load qd_trix.lsp (load "qd_trix")
Then from command line, type quadratrix_2 for drawing quadratrix for 1000 division.
test_1 & test_2 for drawing manually.
If OP & OB are x & y axis respectively, the curve is expressed as y = x tan(p*y/2)
Using identity tan(a) = sin(a)/cos(a), and replacing (p/2)y = h
x = (2/p)*cos(h)*(h/sin(h))
As h approaches zero, both cos(h) and (h/sin(h)) approach 1.
So the x-coordinate of the point R,where the Quadratrix intersect X-axis is (2/p).
This means that length OR is used to get p value, and we now have succeeded in "Squaring the Circle".
This is the reason why this curve is named "Quadratrix", i.e. curve for circle quadrature.
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Jan 22, 2007
Copyright 2006 Takaya Iwamoto All rights reserved.