Squaring the Circle

Go to Fun_Math Content Table Three Famous Problems

Greek Circle Squarers

1. Quadratrix-Hippias

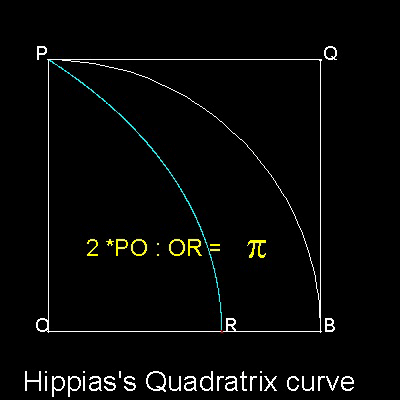
Hippias's(about 460BC-about 400BC) invented a curve now called "Quadratrix", because it can be used for rectifying a circle.
But Hippias invented this curve for Angle Trisection, and called it "Trisectrix".
It is not clear whether Hippias himself knew that this curve can be used to solve "Squaring Circle".

******* Hippias_circle_squarer_desc.dwg ******

For detail, go to the section Hippias-Quadratrix.

2. Archimedes--"On the Measurement of the Circle"

Archimedes (287BC - 212 BC) was the first to give a method of calculating p to any desired degree of accuracy.

His method is based on the fact that the perimeters of the polygons inscribed in a circle and circumscribed about the same circle give lower and upper bound values,respectively, for the circle's circumference.

Examples for hexagon and dodecagon are shown below.

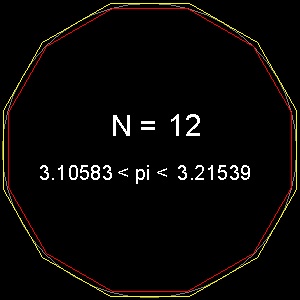
********* pi_hexagon.dwg ********* ********** pi_12gon.dwg *********

In these drawings, the diameter is set to 10. So after opening the drawings, look at the values of perimeter.
(Use either "LIST" command or "Properties" option.)
One tenth (1/10) of the perimeter is the approximation for p .

In modern notation

His idea in modern notation is
n(2)^ksin(q/2^k) < p < n (2)^k tan(q/2^k)
where n is the number of sides in polygon, and q is the angle p/n.
k is the number of times "n" is doubled.e.g. k = 2 means number of sides in polygon is n x 4.
Archimedes chose n = 6 for a starting polygon.
So this can be rewritten as
6(2)^ksin((q/6)/2^k) < p < 6 (2)^k tan((q/6)/2^k)

He increased the number of sides for the polygon up to 96(k = 4), and obtained the following result.
3 (10/71) < p < 3 (1/7)
or in decimal,
3.14084 <p < 3.142858
This is an amazing feat considering that computation was done using ratio's(for example square root 3 was replaced by 265/153, etc) and trigonometry was invented 1000 years after his time.

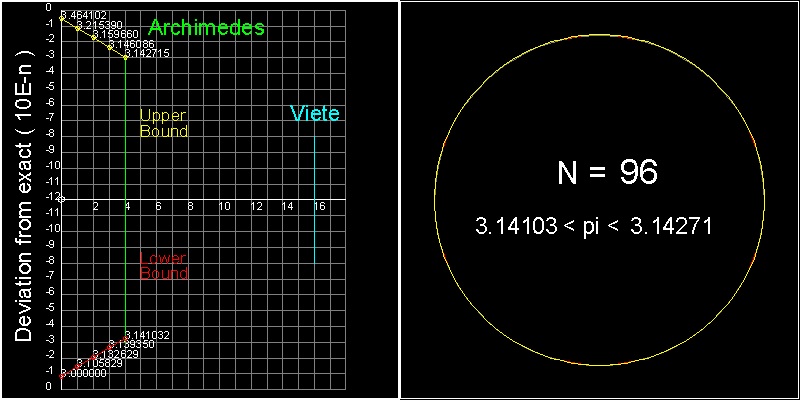
******************************** Archimedes_96_gon.dwg ********************************

You can see the process in animation.

Further improvement by Fibonacci,Viète,Roomen and Ludolph

Almost 18 centuries after Archimedes, mathematicians revisited the Archimedean concept for pi approximation and by using trigonometry, computed the lower and upper bounds with more accuracy.

For detail, go to the section Archimedes_Polygon Approximation.

3. Archimedes--"On Spirals"

Archimedes (287BC - 212 BC) ,in his book "On Spirals", used a spiral to get the length of pi.

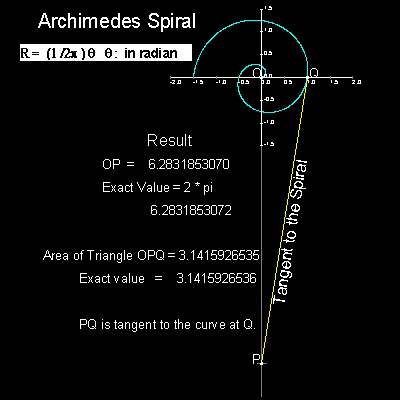
You can see the process in animation.

For detail, go to the section Archimedes Spiral.

References

Heath,Thomas L. :"History of Greek Mathematics Vol. I From Thales to Euclid" Dover 1981

Go to Fun_Math Content Table Three Famous Problems

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006