Squaring the Circle
Go to   Fun_Math Content Table   Three Famous Problems   Greek Circle Squarer

Greek Circle Squarers

Archimedes--Used Spiral

Conon of Samos (about 280BC - about 220 BC) invented a spiral,the polar equation of which is written as r = a q.
This curve was used by Archimedes (287BC - 212 BC) for squaring the circle.
Nowadays this curve is called Archimedean Spiral. 

 
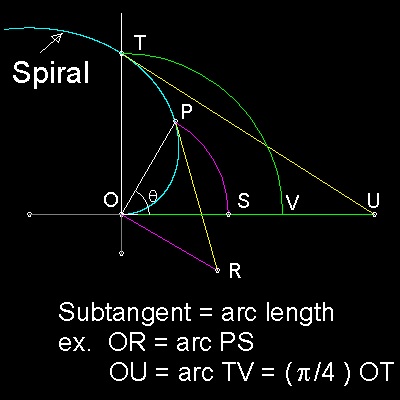
 In his book "On Spiral" Archimedes proves that 
if r is the radius vector to the point P,


OR = r2/a = (a q) (q) = r q = arc length of PS


Point R is a intersection of tangent line at P, 
    and a line drawn at O ,perpendicular to OP.


Line OR is called "subtangent".

If this result is applied to the tangent line at T,
we have   OU = arc length TV = (p/4) OT

This means that the subtangent after one turn(q = 2p)
will be 2p times the radius.

*********** spiral_subtangent.dwg ************

To create this drawing :
   Load sqr_circle.lsp    (load "sqr_circle")
  Then from command line, type spiral_a
This will create a Archimedean spiral with incremental angle of 0.001 radian.
Explode the polyline into many small segements, and
extend these small line segements to draw tangent lines at point P and T.
Open spiral_subtangent.dwg and find out the lenghts of OR,OU, and arc length using LIST command.

How to get a line segment with length of p

From the argument above, it is now possible to get a line segment with length p.
These are the steps to follow:
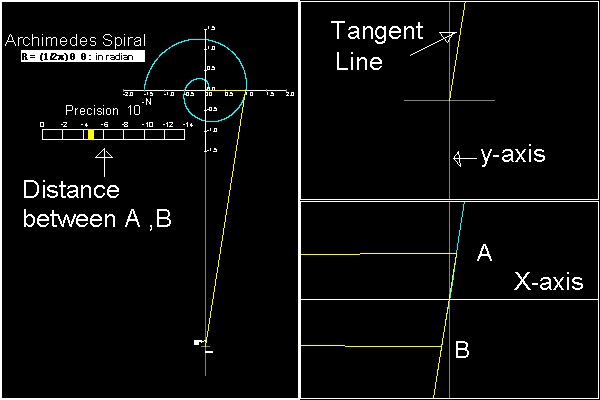
(1) Draw an Archimedean spiral,starting from point O (at x = y = 0).
Note:for convenience, choose constant "a" such that x-value will be 1.0 when x = 2p
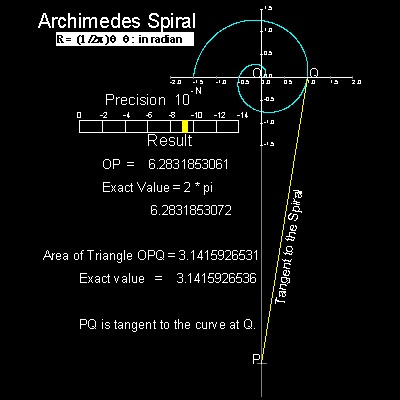
(2) After one turn, the curve cuts x-axsi at point Q.(OQ = 1)
(3) At point Q, draw a tangent line.
(4) This tangent line intersects y-axis at point P.
Length of OP is p
This is equal to the perimeter of a circle with radius OQ.

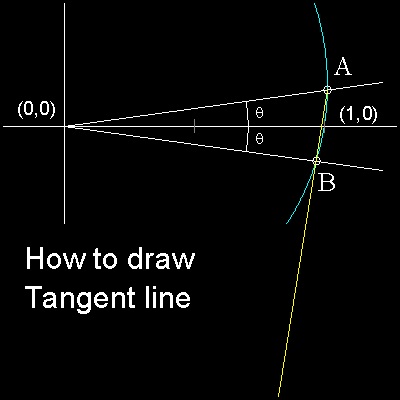
Drawing a tangent line needs some explanation.
Theorectically speaking, tangent line is defined as a limit of angle q approaching zero.
In computer programming, this is accomplished by zooming to the point (1,0),
and making the angle q smaller and smaller.
************** tangnet_line.dwg ***************

3 View ports are used


************** Archimedes_circle_squaring_desc.dwg ***************

Result display

You can see the process in animation.

To create this drawing and animation:
   Load sqr_circle.lsp    (load "sqr_circle")
  Then from command line, type sqr_circle
To create jpg files for animation,type make_anim_jpg
*** Archimedes_circle_squaring_result.dwg ****

References

  1. Heath,Thomas L. :"History of Greek Mathematics Vol. I From Thales to Euclid" Dover 1981

  2. Heath,Thomas L. :"A Manual of Greek Mathematics" Dover 1963 original 1931

  3. Heath,Thomas L. :"A History of Greek Mathematics Vol. II" Dover 1981 original in 1921

  4. Heath,Thomas L. :"The Works of Archimedes Dover" 2002 original in 1912

  5. Knorr,Wilber Richard :"The Ancient Tradition of Geometric Problems" Dover 1993

  6. Knorr,Wilber Richard :"The Textual Studies in Ancient and Medieval Geometry",Birkhauser, 1989
Go to   Fun_Math Content Table   Three Famous Problems   Greek Circle Squarer

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved. .