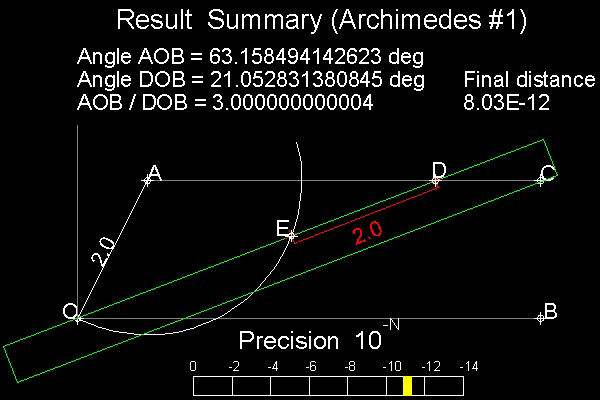
Archimedes' Solution is shown in the figure shown below.

Angle AOB is to be trisected. Draw a line AC parallel to B
Draw a circle with radius = OA with center at A.
Bring a straight-edge marked with ED = OA
Move this ruler such that it passes through point O, "E" on the circle , and "D" on the line AC.
When it is done, angle DOB is 1/3 of angle AOB
Why ?
Hint: AO = AE = ED---> Trangles AOE & AED are isosceles.
************************* trisect_Archimedes_1.dwg *****************
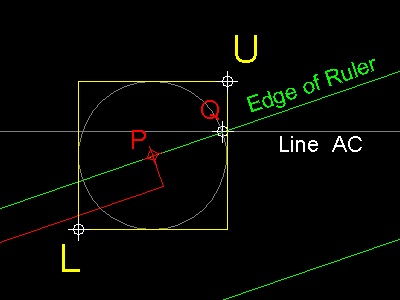
1. It passes through point "O"
2. Point "E" is always on the circle
Then the problem is reduced to make the point "D" as close as possible to the line AC
This is done by checking the distance from point "D" to line AC and keep zooming to point "D".
Without zooming the best human eyes can do is about one hundredth of line length OA.
By continuous zooming centered on the point "D" , the distance, shown in the precision bar in yellow
can be pushed to 10e-12(10 raised to the power of -12) which is close to the limit of program's precision.
*************** auto_zoom.dwg **************
You can see the process in animation.
To create this drawing and animation:
Load neusis.lsp (load "neusis")
Then from command line, type neusis_1
Pappus' Solution is shown in the figure shown below.
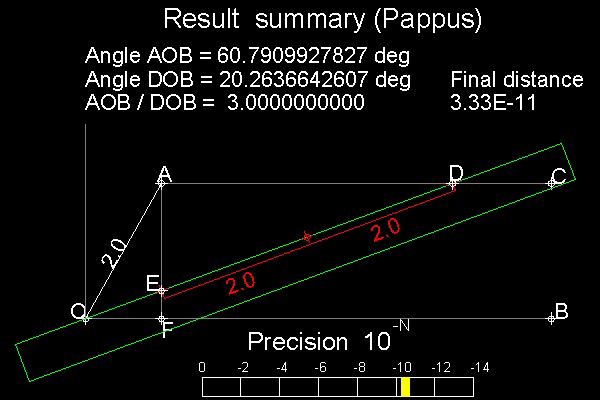
Angle AOB is to be trisected. Draw a line AC parallel to B
Draw a line AF perpendicular to OB, F on the line OB.
Bring a straight-edge marked with ED = 2 * OA
Move this ruler such that it passes through point O, "E" on the line AF , and "D" on the line AC.
When it is done, angle DOB is 1/3 of angle AOB
Why ? Hint: Since angle EAD is 90 degrees, 3 points A,D, E is on the circle with diamter ED.
So the center of the circle and these 3 points make 2 isosceles triangles.
************************* trisect_Pappus_1.dwg *******************
1. It passes through point "O"
2. Point "E" is always on the line AF
Then the problem is reduced to make the point "D" as close as possible to the line AC
This is done by checking the distance from point "D" to line AC and keep zooming to point "D". Without zooming the best human eyes can do is about one hundredth of line length OA. By continuous zooming centered on the point "D" , the distance, shown in the precision bar in yellow can be pushed to 10e-12(10 raised to the power of -12) which is close to the limit of program's precision.
You can see the process in animation.animation
To create this drawing and animation:
Load neusis.lsp (load "neusis")
Then from command line, type neusis_2
Archimedes' Solution is shown in the figure shown below.
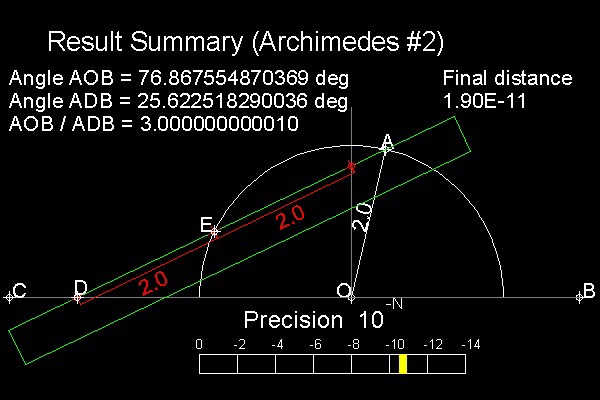
Angle AOB is to be trisected. Draw a line AC parallel to B
Draw a circle with radius = OA with center at O. Additionmal marker beyond "E" is for reference purpose.
Bring a straight-edge marked with ED = OA
Move this ruler such that it passes through point O, "E" on the circle , and "D" on the line AC.
When it is done, angle DOB is 1/3 of angle AOB
Why ? Hint: AO = EO = ED---> Trangles OAE & EDO are isosceles.
Compare this with the above 2 methods. You will see the similarity.
************************* trisect_Archimedes_2.dwg *******************
1. It passes through point "A"
2. Point "E" is always on the circle
Then the problem is reduced to make the point "D" as close as possible to the line BC
This is done by checking the distance from point "D" to line BC and keep zooming to point "D". Without zooming the best human eyes can do is about one hundredth of line length OA. By continuous zooming centered on the point "D" , the distance, shown in the precision bar in yellow can be pushed to 10e-12(10 raised to the power of -12) which is close to the limit of program's precision.
You can see the process in animation.animation
To create this drawing and animation:
Load neusis.lsp (load "neusis")
Then from command line, type neusis_3
1. Yates,Robert Carl : "The Trisection problem"
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.