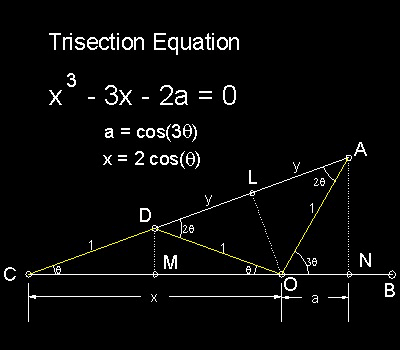
Archimedes' Solution is shown in the figure shown below.

Since three triangles CDM, COL and CAN are similar. CM/CD = CL/CO = CN/CA.
So x/2 = (1 + y)/x = (x + a)/(1 + 2y)
which gives ---> x2 = 2 + 2y and 1 + 2y = 2(x + a)/x
Eliminating y from these two equations, we obtain x 2 - 1 = 2(x + a)/x or
x 3 - 3x - 2a = 0
where x = 2cos(q) and a = cos(3q)
Using the trigonometric identities, cos(a+b) = cos(a)cos(b) - sin(a)sin(b) and sin(2a) = 2*sin(a)cos(a)
cos(3q) = 4cos3 (q) - 3 cos (q)
Using the relations (Refer to the figure); x = 2cos(q) and a = cos(3q)
This equation can now be written as
x 3 - 3x - 2a = 0
Therefore a + x = (1 + 2y)*cos(q) , and y = DO *cos(2q)
From these relations, the same trisection equation can be derived.
1. Yates,Robert Carl : "The Trisection problem"
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.