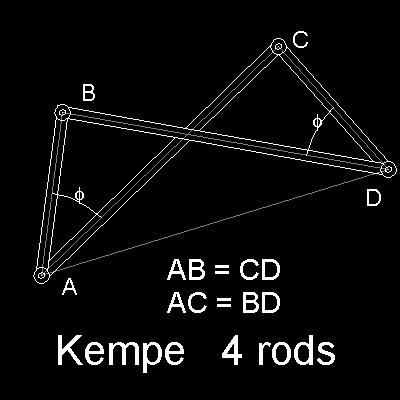
Kempe's Link is shown in the figure shown below.

In this simple link, the length of 4 rods are set such that
AB = CD and AC = BD.
Then, when D moves with point A as a pivot,
angle BAC is always equal to angle BDC.
You can see the process in animation
****** Kempe_4_rods_desc.dwg ******
To create this drawing and animation:
Load Kempe_4_rods.lsp (load "Kempe_4_rods")
Then from command line, type 4_rods
Animation file creation:animation_4_rods
Kempe's Link is shown in the figure shown below.
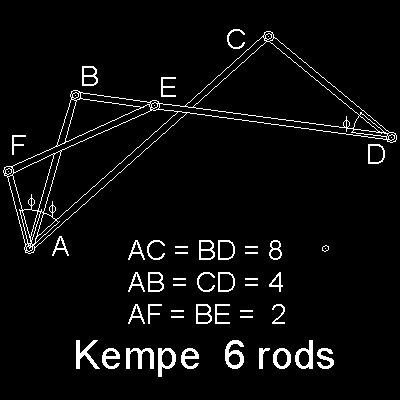
Two more rods (AF & FE) are added such that
trapezoid ABCD and AFBE are similar.
When this link is moved around pivot point at A
angle FAb = angle BAC = angle BDC.
Link AB is a angle bisector of angle FAC.
You can see the process in animation
****** Kempe_6_rods_desc.dwg ******
To create this drawing and animation:
Load Kempe_6_rods.lsp (load "Kempe_6_rods")
Then from command line, type 6_rods
Animation file creation:animation_6_rods
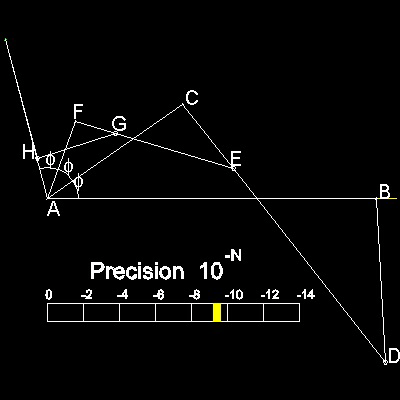
Kempe's Link is shown in the figure shown below.
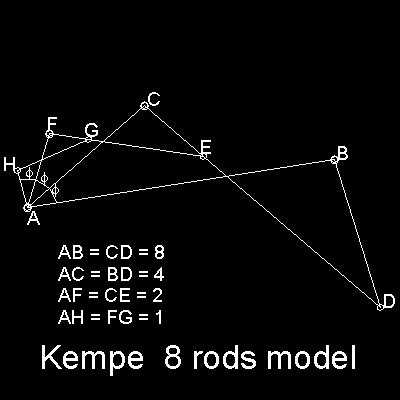
2 more rods are added to the linkage.
Now there are 3 similar trapezoids,AHFG, AFCE and ACBD.
When this linkage is moved around the pivot A
angle HAF = angle FAC = angle CAB = (1/3) angle HAB
i.e., angle HAB is trisected by this linkage.
You can see the process in animation
****** Kempe_8_rods_desc.dwg ******
To create this drawing and animation:
Load Kempe_8_rods.lsp (load "Kempe_8_rods")
Then from command line, type 8_rods
Animation file creation:animation_8_rods
Kempe's Link is shown in the figure shown below.
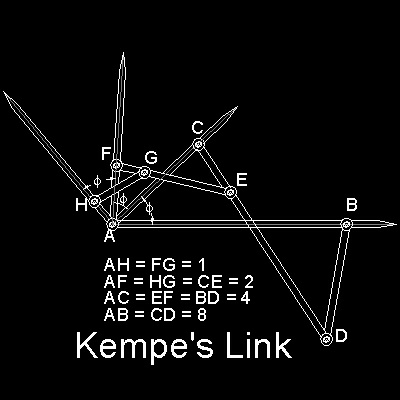
You can see the process in animation.animation
****** link_Kempe_desc.dwg ******
To create this drawing and animation:
Load link_Kempe.lsp (load "link_Kempe")
Then from command line, type link_Kempe
For a quick look to see how the mechanism works, type test_Kempe
Animation file creation:animation_Kempe
---->input @4<105. -->105 degrees case
****** Kempe_trisection_105_deg.dwg ******
1. Robert C.Yates:"The Trisection problem",p 39 - 41
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.