Trisection using mechanical links

1. Ceva's Pantograph

Tomasso Ceva (1648 - 1737) published trisecting tool named "Ceva's Pantograph" in 1695.
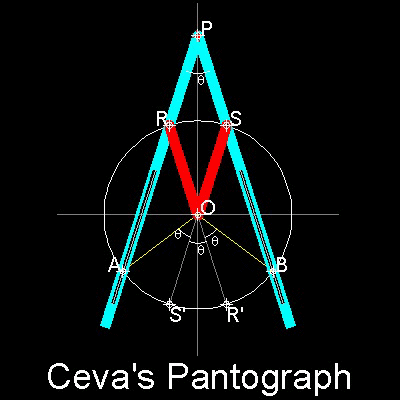
Ceva's Pantograph is shown in the figure shown below.

Angle to be trisected is AOB.

Point O is a fixed point,and point P moves along the line PO.

PR = PS = RO = SO. Points R & S moves along the circle.

Trisection of the angle AOB is done when the line extending PR passes through

the point "A".

You can see the process in animation.

For detail, go to the section Ceva's Pantograph.
*********** pantograph_desc.dwg ***********

2. Amadori's Link

Amadori's Link is shown in the figure shown below.

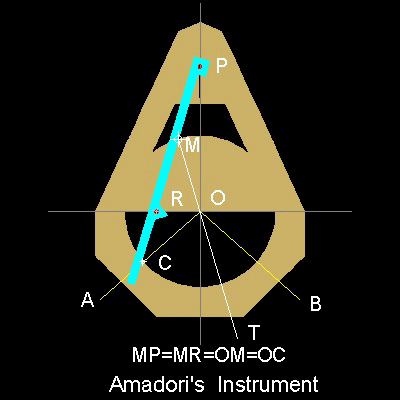
The principle used for Amadori's Link is the same as the one applied for Ceva's Pantograph decribed above. The straight edge is attached to a base plate which has a cutout circle. The point P of the stright edge moves along the bisector of the angle AOB while point R moves along the diameter of the circle. The trisection is accomplished when the line PR passes through point C.

You can see the process in animation.

For detail, go to the section Amadori's Link.
*********** Amadori_desc.dwg ***********

3. Laisant's Links

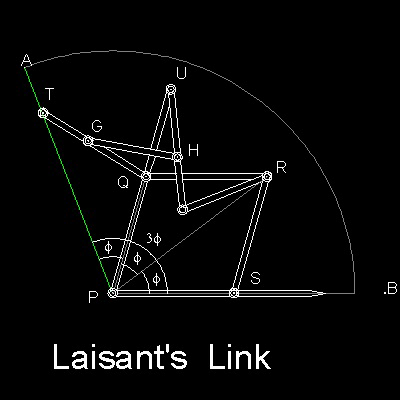
One of the Laisant's Link is shown in the figure shown below.

You can see the process in animation.

For detail, go to the section Laisant's Links.
*********** Laisant_desc.dwg ***********

4. Kempe's Links

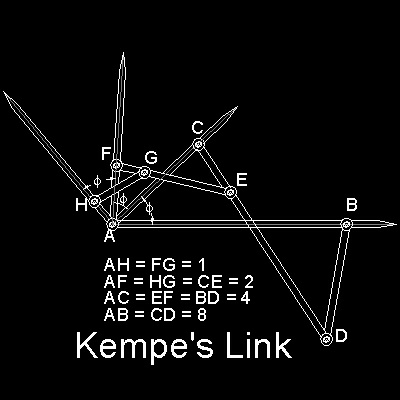
Kempe, Alfred Bray (1849 - 1922) published a very unique linkage used for angle trisection in 1875.
Kempe's Link is shown in the figure shown below.

You can see the process in animation.

For detail, go to the section Kempe's Links.
*********** link_Kempe_desc.dwg ***********

5. Sylvester's Link_Fan

Sylvester,James Joseph (1814 - 1897) announced a linkage trisector,which he named "A Lady's Fan" ,in 1875.
Sylvester's Link is shown in the figure shown below.

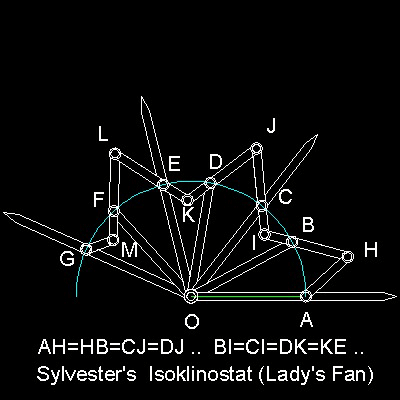
You can see the process in animation.

For detail, go to the section Sylvester's Isoklinostat.
*********** link_fan_desc.dwg ***********

6. Line Motion Trisector

Line Motion Trisector is shown in the figure shown below.

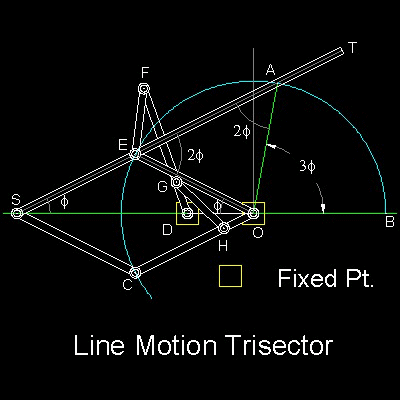
You can see the process in animation.

For detail, go to the section Line Motion Trisector.
*********** link_motion_desc.dwg ***********

References

1. Yates,Robert Carl: "The Trisection problem",pp.31-46

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved. .