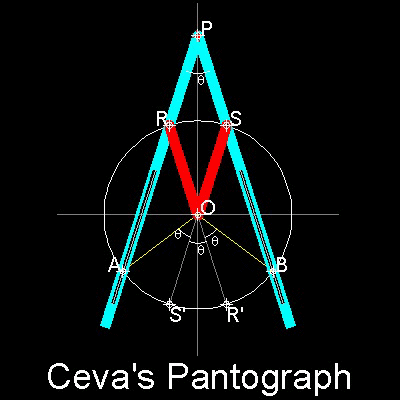
Ceva's Pantograph is shown in the figure shown below.
Tommaso Ceva (1648-1737)
was an Italian Jesuit who worked in geometry,gravity and arithmetic.
His brother Giovanni Ceva (1647-1734)
is well known for his Ceva's Theorem and rediscovery & publishing of Menelaus' Theorem.

Angle to be trisected is AOB.
Point O is a fixed point,and point P moves along the line PO.
PR = PS = RO = SO. Points R & S moves along the circle.
Trisection of the angle AOB is done when the line extending PR passes through
the point "A".
You can see the process in animation.
*********** pantograph_desc.dwg ***********
To create this drawing and animation:
Load pantograph.lsp (load "pantograph")
Then from command line, type pantograph
For a quick look to see how the mechanism works, type test_pantograph
During the program execution, three viewports like shown will appear. Program will detect cursor move in the view port ,centered at the top (point P) .
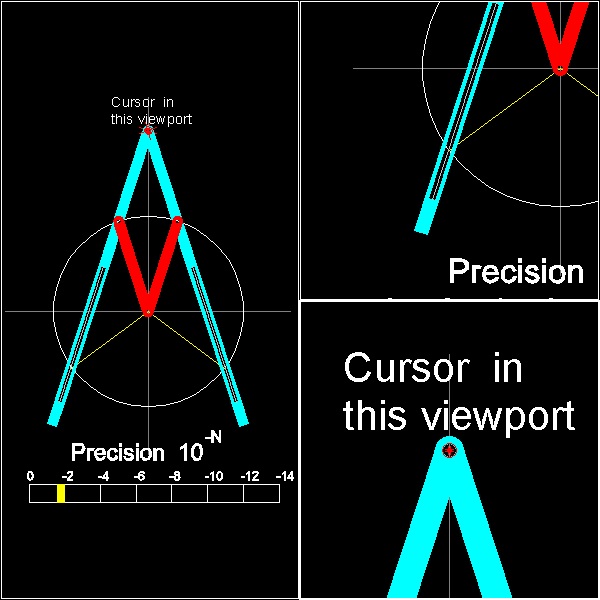
*********** pantograph_note.dwg ***********
The idea of Ceva's Pantograph is coming from a simple three bar link as shown below ,which is also credited to Ceva.
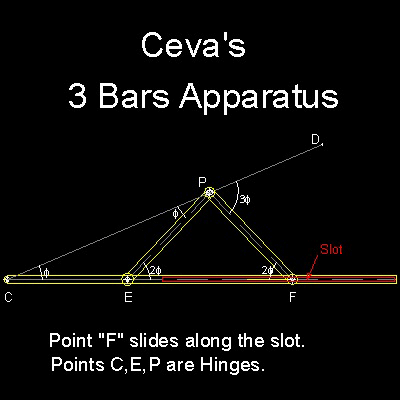
Length of bars EP and FP are equal to the distance CE.
Bar CF has a groove so that point "F" moves freely along the line CF.
Comparing this figure with the Insertion methods by Archimedes, it is easy to see angle PCF is always 1/3 of angle DPF.
You can see the process in animation.
*********** 3bars_apparatus.dwg ***********
To create this drawing and animation:
Load link_Ceva1.lsp (load "link_Ceva1")
Then from command line, type link_Ceva1
For a quick look to se how the mechanism works, type test_Ceva1
Animation file creation:animation_link_ceva1
When the above mentioned Ceva's 3 Bars Apparatus is placed upside down(as shown below), and the point O is fixed at the center of a circle , then this also can be used as an Angle Trisection tool.
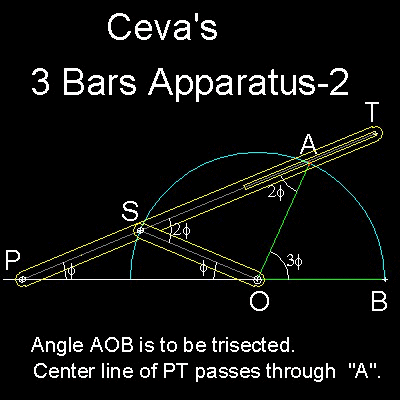
Length of PS, SO and OA are all equal.
The trisection of the given angle AOB is done when the center line of bar PT passes through the point A marked on the circle,the radius of which is equal to PS and SO.
You can see the process in animation.
*********** 3bars_apparatus_2.dwg ***********
To create this drawing and animation:
Load link_Ceva2.lsp (load "link_Ceva2")
Then from command line, type link_Ceva2
For a quick look to se how the mechanism works, type test_Ceva2
1. Yates,Robert Carl:"The Trisection Problem", pp 34-35.
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.