Tomasso Ceva (1648 - 1737) applied "Insertion method" by Archimedes to Angle trisection using a special curve called "Cycloidum anomalarum", or "The Cycloid of Ceva".
The idea is shown in the figure shown below.

An equation of the curve in polar coordinate is:
r = 1 + 2 cos(q),
and in rectangular coordinate:
(x2 + y2)3 = (3x2 - y2)2
See how the curve is drawn by animation.
******** cycloid_of_Ceva.dwg ********
To create this drawing and animation:
Load cycloid_Ceva.lsp (load "cycloid_Ceva")
Then from command line, type draw_cycloid_Ceva_only

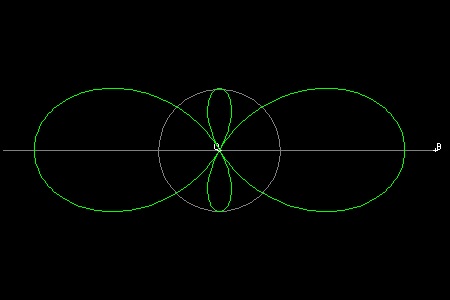
The link CQPD are made up of 3 links CP, QD and DP. P slides along line connecting CQ, and D slides along line CD(x-axis).When Q moves along a unit circle with its center at C, the locus of point P makes a 4-leaves curve as shown. This is called "The Cycloid of Ceva".
See how the curve is drawn by animation.
Trisection Procedure:
Angle AOB is to be trisected.
Draw a line through D parallel to line AO.
It intersects the curve at point P.
Line PC trisects the angle AOB.
******** cycloid_of_Ceva_tri_desc.dwg ********
This curve is of the sixth degree, and for a given value of y, it generally has 6 x-values as noticed in the figure for trisection.
To create this drawing and animation:
Load cycloid_Ceva.lsp (load "cycloid_Ceva")
Then from command line, type Ceva_trisection
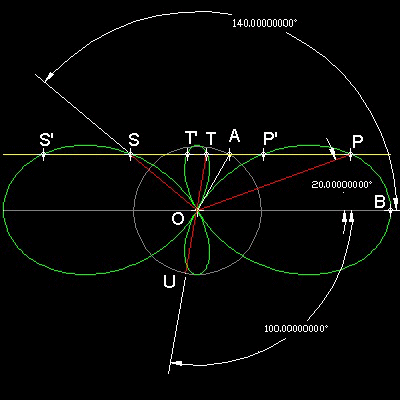
In order to explain the interpretation of 6 intersecting points (P, S, T and P',S', T') the case of 60 degrees is shown in the figure. The 3 solutions for Trisecting angle 3q = 60 degrees are:
POB = q = 20 degrees
SOB = (1/3)(360 + 3q) = 120 + q = 140 degrees
BOU(clockwise) = (1/3)(720 + 3q) = 240 + q = 260 degrees,or, 100 degrees clockwise,where U is the point where the extension of line TO meets a unit circle.
Similarly P',S' and T' are for the case 3q = 180 - 60 = 120 degrees.
*** cycloid_Ceva_trisection_60_deg.dwg ***
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.