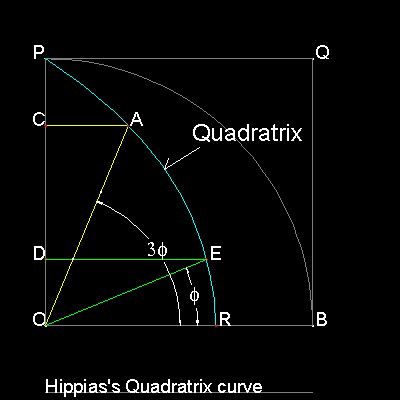
Hippias's(about 460BC-about 400BC) Trisection method is shown in the figure shown below.
The procedure for Trisection is:
Step 1:Draw the quadratrix , then select a point "A" on this curve to define angle AOB
Step 2:Draw a line from "A" parallel to AB and the intersection with line PO is point "C".
Step 3:Find a point "D" on line CO such that OD = CO/3
Step 4:Draw a line from "D" parallet to OB, and find a point "E" ,intersecting this curve.
Angle EOB trisects angle AOB.
*********** quadratrix_tri_desc.dwg ***********
You can see the process in animation. For detail, go to the section Quadratrix - Hippias.
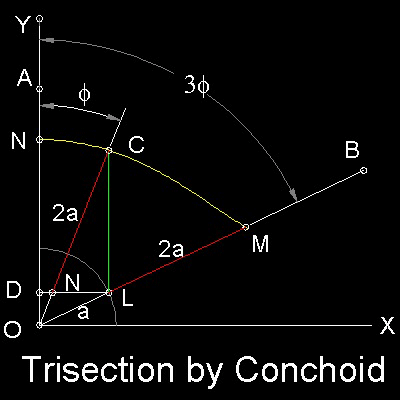The Trisection procedure is:
Step 1: Draw a rectangular coordinate Axis O-XY, and locate Point "A" on OY. Draw a line OB to define angle AOB. Angle AOB is to be trisected.
Step 2: Draw a unit radiuds(a) circle at "o", and "L" is the intersection of this circle and line OB. Draw a line from "L" parallel to OB and it intersects Y axis at point "D".
Step 3:Draw a "Conchoid" with "O" as a pole, line "DL" as "ruler" and fixed length = 2a.The resulting curve is NCM.
Step 4:Draw a line form "L" parallel to Y axis and it intersects this Conchoid at point "C". Line OC trisects angle AOB.
******** conchoid_trisection_desc.dwg ********
You can see the process in animation. For detail, go to the section Conchoid - Nicomedes.
Archimedes(287 BC - 212 BC) used Spiral (called Archimedes' Sprial) for Trisection. His idea is shown in the figure shown below.
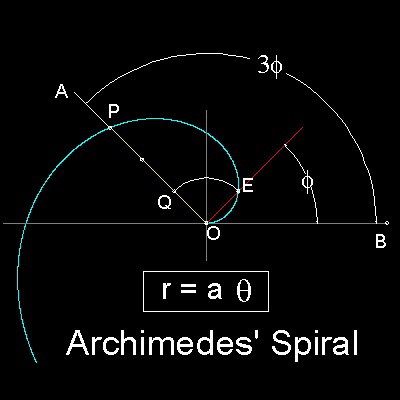
You can see the process in animation. For detail, go to the section Spiral - Archimedes.
Pappus(280 - 350) showed that "Huyperbola" can be used for Angle Trisection. His idea is shown in the figure shown below.
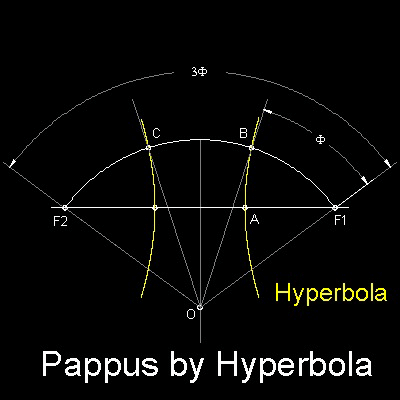
The trisection of angle F1-O-F2 is equivalent to dividing arc F1-F2 into 3 equal arc length.
This is accomplished by using the hyperbola with eccentricity equal to 2.
It measn that for all the points on the hyperbola the distance from the F1(called Focus) is two times the normal distance to
Y-axis(called Directrix). Because of symmetry the intersecting points B & C divides arc F1-O-F2
into 3 equal length arcs.
******** Pappus_hyperbola_tri_desc.dwg ********
You can see the process in animation. For detail, go to the section Hyperbola - Pappus.
Limaçon was invented by Blaise Pascal (1623 - 1662) about 1650, and used by Isaac Newton (1643 - 1727) for Angle Trisection. The idea is shown in the figure shown below.
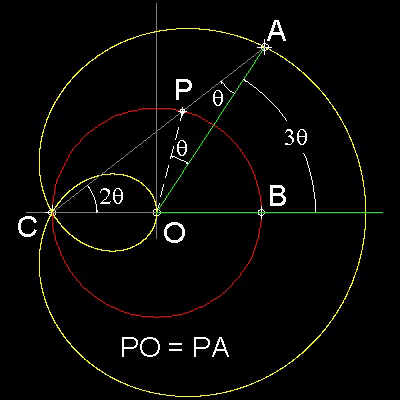
Point "P" moves along a circle of unit radius CO. Let b be a fixed length. Extend CP and produce point "A" such that PA = b. Then the loucs of "A" is a Limaçon. The type of Limaçon used for Trisection is b = 1 case. The yellow colored curve is the Limason Pascal used to Trisection.
Draw a unit circle with its center at "O". Draw a Limaçon with fixed length b = 1.
Select a point "A" on the Limaçon to define an angle AOB to be trisected.
Draw a line CA. Angle CAO is the angle trisected.
******** limason_tri_desc.dwg ********
You can see the process in animation. For detail, go to the section Limaçon - Pascal.
Rene Descartes(1596 - 1650) ,who is called the founder of the "Analytic Geometry",published the famous treatise "La Geometrie" in 1637. In this book he showed that Angle Trisection can be done by using Parabola. His idea is shown in the figure shown below.
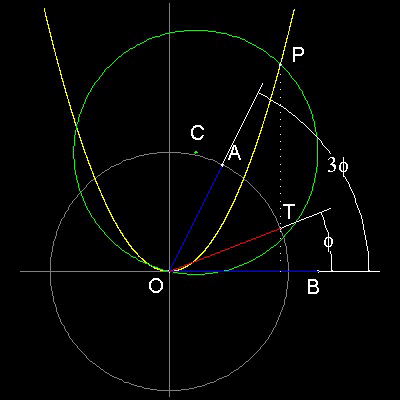
2. Drop the perpendicular from A to OB. Let the length be 2a (in Trisection equation)
3. Draw a parabola y = x2. Draw a circle with its center at point C (a, 2)
4. Get intersecting point "P", and drop the perpendicular to OB. This will cut the circle drawn at step 3 at point "T"
5. The line OT is a trisector of angle AOB.
******** parabola_tri_desc.dwg ********
You can see the process in animation. For detail, go to the section Parabola - Rene Descartes.
The idea of using Parabola can be easily extended to "Cubic parabola". The idea is shown in the figure shown below.
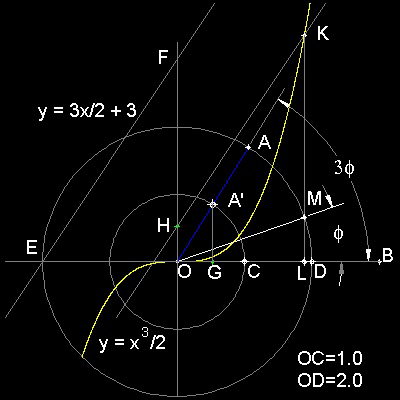
2. Pick a point "A" on the outer circle to define angle AOB for trisection. OA intersects the inner circle at A'. Drop a line from A'perpendicular to OB. Intersection is G. Note here that length OG is "a" in Trisection Equation.
3. Get a point H on Y-axis, such that OH = OG. Draw a line through point H parallel to line EF.
. 4. This line will cut the cubic parabola at point K. Drop a line perpendicular to OB. This intersects the inner circle at point M. Line MO is the trisector of angle AOB.
******** cubic_parabola_tri_desc.dwg ********
You can see the process in animation. For detail, go to the section Cubic Parabola.
Tomasso Ceva(1648 - 1737) ,brother of Giovanni Ceva(1647 - 1734) ,who is known for Ceva's theorem, applied "Insertion method" by Archimedes to Angle trisection using a special curve called "Cycloidum anomalarun", or "The Cycloid of Ceva".
The idea is shown in the figure shown below.
2. Define angle AOB
3. get unit length OE on line OA, and draw a parallel line to OB through point E.
4. This line cuts "Cycloid of Ceva" at 6 places. P,S and T are for trisectiong angles 3q , 360 deg + 3q , and 720 deg + 3q , respectively.
The remaining 3 points P', S' and T' are for 180 - 3q,
******** cycloid_of_Ceva_tri_desc.dwg ********
You can see the process in animation. For detail, go to the section Cycloidum Anomalarum - Ceva.
Colin Maclaurin (1698-1746),who is known for Maclaurin Series, used a curve called "Trisectrix" to accomplish Angle Trisection.
His idea is shown in the figure shown below.
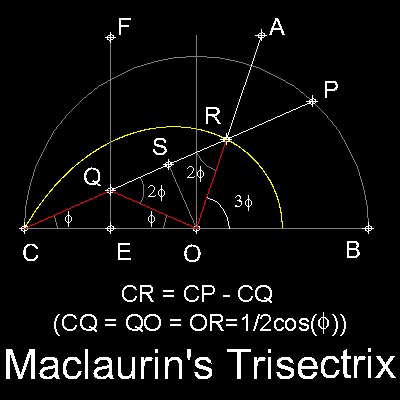
2. Pick a point Q on EF, and P is the intersection of CQ and the semi_circle.
3. Locate a point R such that CR = CP - CQ is satisfied.
4. Locus of R as point Q moves along the line EF is the curve called "Maclaurin's Trisectrix".
Note: This process is also interpreted as a "imaginary" link CQ-QO-OR as Q moves along EF. It is "imaginary" because the length of the link is variable, and in reality, it does not exist.
******** Maclaurin_tri_desc.dwg ********
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.
