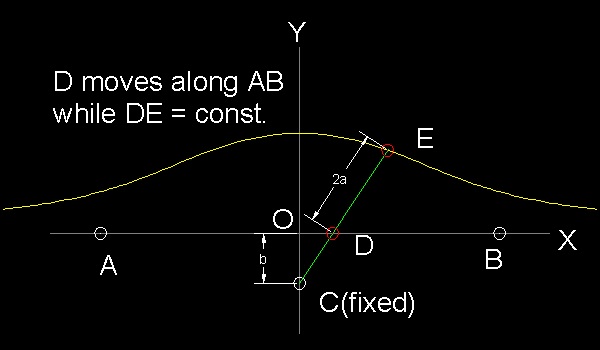
point D moves along the line AB(called "ruler") around the pivot C (called "pole")
The length of DE is constant. The locus of E is called Conchoid.
*********************** conchoid_curve.dwg ***********************
This curve was first called "Cochloid", then later named "Conchoid". It was invented by Nicomedes to solve the "Delian Problem", but later Pappus found out that it can be used for Angle Trisection.

point D moves along the line AB(called "ruler") around the pivot C (called "pole")
The length of DE is constant. The locus of E is called Conchoid.
*********************** conchoid_curve.dwg ***********************
To draw a conchoid by selecting "Pole" and two end points of "Ruler":
Load utility_curves.lsp
(load "utility_curves")
Then from command line, type test_conchoid
Trisection using Conchoid is shown in the figure shown below.
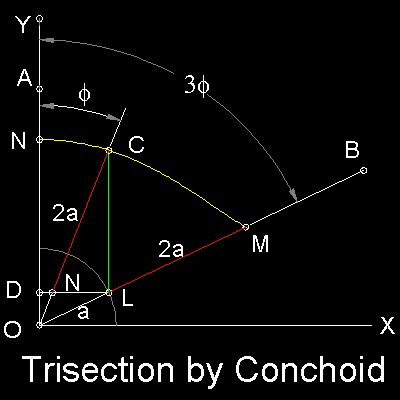
The Trisection procedure is:
Step 1: Draw a rectangular coordinate Axis O-XY, and locate Point "A" on OY. Draw a line OB to define angle AOB.
Angle AOB is to be trisected.
Step 2: Draw a unit radius(a) circle at "O", and "L" is the intersection of this circle and line OB. Draw a line from "L" parallel to OB and it intersects Y axis at point "D".
Step 3:Draw a "Conchoid" with "O" as a pole, line "DL" as "ruler" and fixed length = 2a.The resulting curve is NCM.
Step 4:Draw a line form "L" parallel to Y axis and it intersects this Conchoid at point "C". Line OC trisects angle AOB.
This is the animation.
******** conchoid_trisection_desc.dwg ********
In general , if we let OD=b, the polar equation for conchoid is r = b/cosf + 2a
The rectangular equation is (x2 + y2)(y - b)2 = 4a2y2
To create this drawing and animation:
Load nicomedes.lsp and utility_curves.lsp
(load "nicomedes") and (load "utility_curves")
Then from command line, type conchoid_trisection .
This will excute a step by step trisection process.
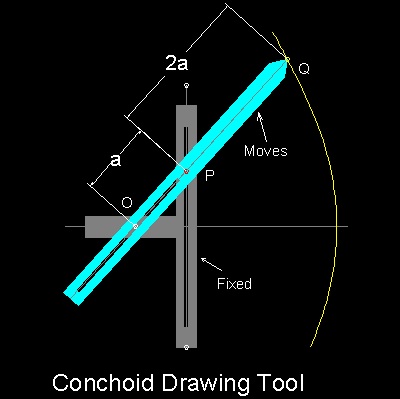
The tool to draw "Conchoid" was also invented. As shown , it has one fixed , and one moving part. There are two pegs at O and P, and O (which is called "Pole") allows the moving part move freely along the slot in the moving part, and P,which is fixed in the moving part can move freely along the slot in the fixed "ruler".In this example length PQ is set to trisect the angle made by OQ and x-axis.(See figure above)
Trisection is complete when the tip of the moving part (Q) comes on the horizontal line passing through point P.
******** conchoid_drawing_tool.dwg ********
As we know already , placing cursor exactly on the line is not easy without zooming operation. The two processes are shown here in animation.
The first case is without ZOOM ,the second with Zoom.
Click the text to see animations.
The first case animation
The second case animation
To create this drawing and animation:
Load nicomedes.lsp and utility_curves.lsp
(load "nicomedes") and (load "utility_curves")
Then from command line, type test_1 and test_2 for two cases.
test_1: Frist case:---Plain trisection without zooming
test_2: Second case:---Refined trisection with zooming
1. Yates,Robert C.:"The Trisection problem",first published in 1942.
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.