Special Curves

Go to Fun_Math Content Table Trisecting an Angle Special Curves

Trisection using Special Curves

The Cubic Parabola

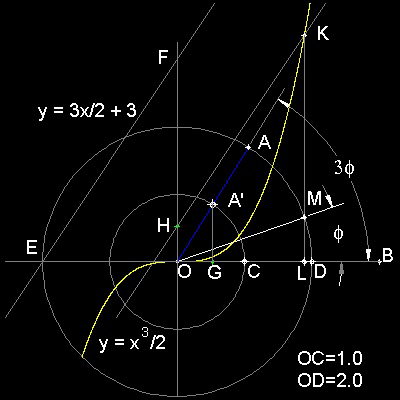
The idea of using Parabola can be easily extended to "Cubic parabola". The idea is shown in the figure shown below.

Formulation of Cubic Parabola

Expanding the idea of the previous method using Parabola, Cubic Parabola can also be used for angle trisection.

Dividing all 3 terms of the Trisection Equation by 2, the result will be

(1/2)x³ = (3/2)x + a

This suggests that the roots of the trisection equation are the x-values of the intersection of cubic parabola and a line cutting y-axis at y = a with its slope = 3/2.
******** cubic_parabola_tri_desc.dwg ********

You can see the process in animation.animation

To create this drawing and animation:
   Load cubic_parabola.lsp    (load "cubic_parabola")
  Then from command line, type cubic_trisection

Example: AOB = 60 degrees case

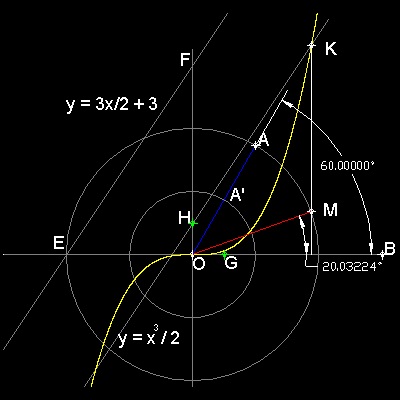
1. Input 2<60. to specify point A
2. Line AO(blue) will cut inner circle at A'.
3. Drop a line from A' perpendiculr to x-axs, and locate point G(green).
4. Find a point H on y-axis such that OG = OH
5. Draw a line through H parallel to a line EF
  ( y = 3x/2 + 3).
6. This line intersects cubic parabola at point K.
7. Drop a line from point K perpendicular to x-axis.
8. This line intersects the outer circle at point M.
9. angle MOB trisects angle AOB.

Question: How about the other two intersecting points ?
** cubic_parabola_trisection_60_deg.dwg **

References

Go to Fun_Math Content Table Trisecting an Angle Special Curves

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006