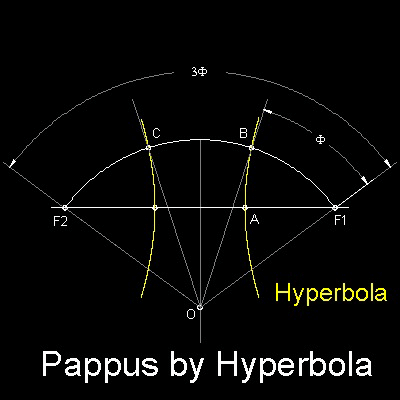
Pappus (280 - 350) showed that "Hyperbola" can be used for Angle Trisection. His idea is shown in the figure shown below.

The general formula for this hyperbola is given by
y2 + (1-e2)x2-2kx + k2 = 0
where k = distance of F1 to directrix (X-coordinate value of point F1) =half the distance between B & C.
and e = eccentricity = 2 in this case.
In general, e> 1 for hyperbola
You can see the process in animation.
For detail, go to the section on Conics.
****** Pappus_hyperbola_tri_desc.dwg ******
To create this drawing and animation:
Load Pappus_hyperbola.lsp (load "Pappus_hyperbola")
Then from command line, type pappus_1
Proof of the trisection is straight forward :
Since the hyperbola is drawn such that half of BC is equal to BF1(= CF2),
these 3 arcs have the same length. Therefore angle F2OC = COB = BOF1 = (1/3)angle F1OF2.
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.