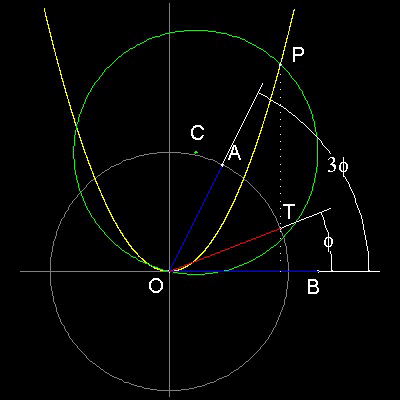
Rene Descartes (1596 - 1650) showed that Angle Trisection can be done by using Parabola. His idea is shown in the figure shown below.
You can see the process in animation.

He showed that both Delian and Trisection problems are equivalent to solving the cubic equations, and its solution are obtained by using conics( parabola is one of them. )
In the case of trisection, the roots of the trisection equation: x3 - 3x -2a = 0 , where a = cos(3q) are represented by the x-coordinate values of intersection of (1) parabola and (2) a circle with its center at point (a, 2).Thus,
(1) y = x2
(2) x2 + y2 - 2ax - 4y = 0
By substituting (1) into (2) ,y is eliminated and the resulting equation only for x is
x ( x3 - 3x -2a ) = 0 , or x3 - 3x -2a = 0
To create this drawing and animation:
Load parabola_trisection.lsp (load "parabola_trisection")
Then from command line, type parabola_trisection
This will let users define angle to be trisected, draw parabola and circle. The rest of the
operaration will be done manually.
Example: AOB = 60 degrees case
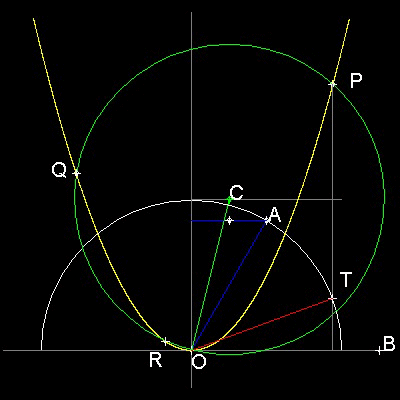
1. Input 2<60. to specify point A
2. Drop a line (blue) perpendicular to y-axis. mark the mid point.
3. Find point C on the line y=1 drawing a line parallel line through the mid point.
4. With the center at C, draw a circle (green) with radius CO.
5. Intersection points between green circle and yellow parabola are P, Q & R.
6. Drop a line from point P perpendicular to x-axis.
7. This line intersects the unit circle at point T.
8. angle TOB trisects angle AOB.
Question: How about points Q & R ?
** parabola_trisection_60_deg_case.dwg **
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.