Special Curves

Limaçon was used by Blaise Pascal (1623 - 1662) for Angle Trisection.
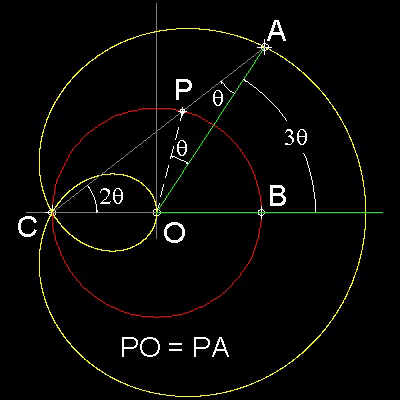
His idea is shown in the figure shown below.

In polar corrdinate: r = 2cos q + b

In rectangular coordinate: (x² + y² - 2x)² = b²(x² + y²)

Since Triangles COP and POA are isosceles,

Ð POA = Ð PAO and Ð OCP = Ð OPC = 2 x Ð PAO

Ð AOB = Ð PCO + Ð PAO = 3 x Ð PAO

Therefore Ð AOB is trisected.

******** limason_tri_desc.dwg ********

You can see the process in animation.

To create this drawing and animation:
Load Pascal.lsp (load "Pascal")
Then from command line, type pascal_5

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006