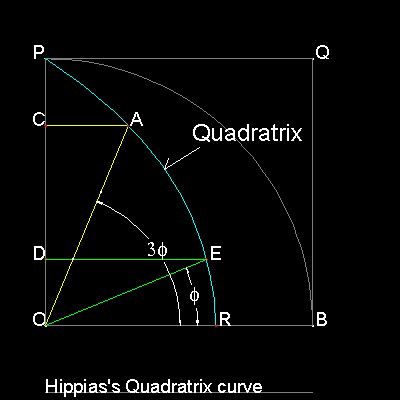
Hippias's(about 460BC-about 400BC) Trisection method is shown in the figure shown below.
The procedure for Trisection is:
Step 1:Draw the quadratrix , then select a point "A" on this curve to define angle AOB
Step 2:Draw a line from "A" parallel to AB and the intersection with line PO is point "C".
Step 3:Find a point "D" on line CO such that OD = CO/3
Step 4:Draw a line from "D" parallet to OB, and find a point "E" ,intersecting this curve.
Angle EOB trisects angle AOB.
You can see the process in animation.
*********** quadratrix_tri_desc.dwg ***********
To create this drawing and animation:
Load qd_trix.lsp (load "qd_trix")
Then from command line, type quadratrix_3
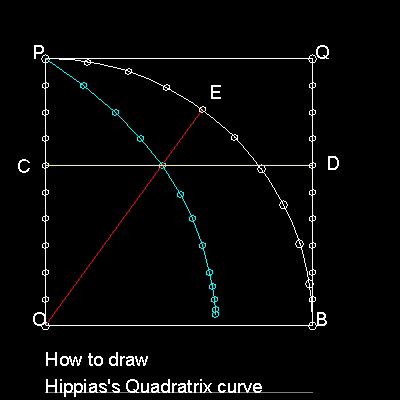OBQP is a square.
Divide both OP and BQ in equal parts N.
Divide a quarter circle BP into the same number N. Point C,D & E arer such points.
Horizontal line CD(yellow) and polar line OE(red) intersect .
The locus of such points(cyan color) is the "Quadratrix".
You can see the process in animation.
*********** quadratrix_curve_10_div.dwg ***********
To create this drawing and animation:
Load qd_trix.lsp (load "qd_trix")
Then from command line, type quadratrix_2 for drawing quadratrix for 1000 division.
test_1 & test_2 for drawing manually.
If OP & OB are x & y axis respectively, the curve is expressed as y = x tan(p*y/2)
Using identity tan(a) = sin(a)/cos(a), and replacing (p/2)y = h
x = (2/p)*cos(h)*(h/sin(h))
As h approaches zero, both cos(h) and (h/sin(h)) approach 1.
So the x-coordinate of the point R,where the Quadratrix intersect X-axis is (2/p).
This means that length OR is used to get p value, and we now have succeeded in "Squaring the Circle". This is the reason why this curve is named "Quadratrix", i.e. curve for circle quadrature.
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.
