Special Curves

Go to Fun_Math Content Table Trisecting an Angle Special Curves

Trisection using Special Curves -Archimedian-Spiral Curves

Archimedian Spiral

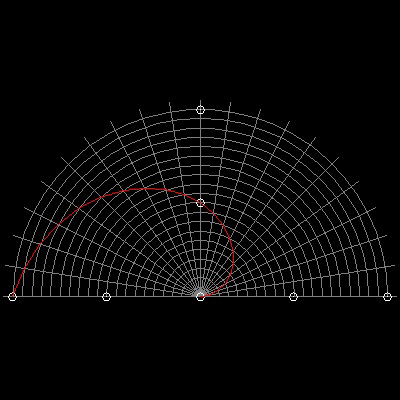
Archimedes (287 BC - 212 BC) used Spiral (called Archimedian Spiral) for Trisection. His idea is shown in the figure shown below.

How to draw Archimedian Spiral manually

Formula for Archimedean Spiral in polar coordinate is
r = a q
where "a" is an constant. Here it is set to be (2/p) . Then the radii of this curve where it cuts X-Y axis is 1, 2, 3 ,4 etc as it goes around anti-clockwise.

The curve is drawn by connecting the intersecting points between concentric circles and lines passing through the center of those circles.

You can see the process in animation.

***** draw_Archimedian_spiral_base.dwg *****

There is a similarity between this curve and Quadratrix. In the case of Quadratrix ,Y-axis length changes linearly, whereas in Spiral case, length of radius changes linearly with angle value.

To create this drawing and animation :
Load utility_curves.lsp (load "utility_curves")
Then from command line, type (concentric_circles) & (multiple_rays)

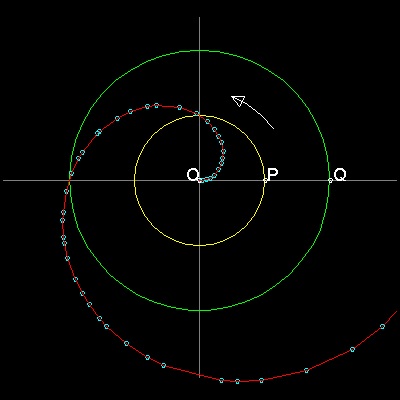
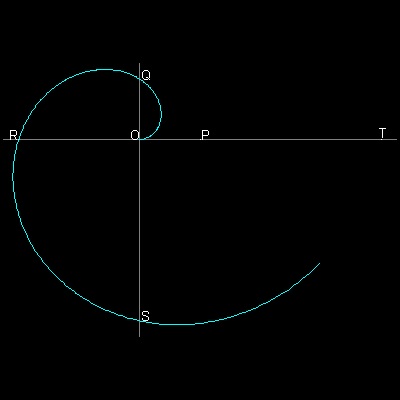
How to draw Archimedian Spiral semi_automatically

*************** spiral_a_1.dwg *************** *************** spiral_a_2.dwg ***************

To create these drawings :
Load spiral_a.lsp (load "spiral_a")
Then from command line, type test_1 & test_2

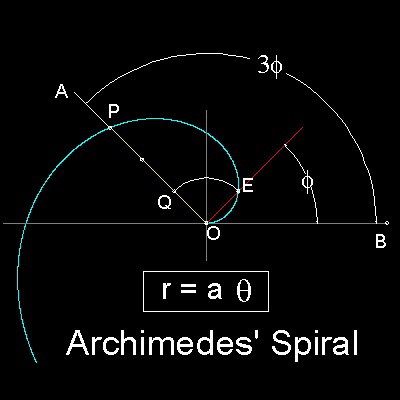
Angle Trisection by Archimedian Spiral

Similarity of Spiral to Quadratrix suggests that this curve can also be used for angle trisection.

The reason it can be used for angle trisection is that since the change in angle is proportional to the change in its radius, division of angle is equivalent to the division of length, which will be an easy process.

You can see the process in animation.

************* spiral_tri_desc.dwg *************

To create this drawing and animation :
Load spiral_a.lsp (load "spiral_a")
Then from command line, type spiral_4

Samples of Archimedes' Spiral

3 Archimedian Spirals after 1 rotation , 6 rotations, and 128 rotations are shown here. As the distance between curves gets closer and closer, Moire fringe-like pattern developes.

************* spiral_2_pi.dwg **************** ************* spiral_12_pi.dwg *************** ************* spiral_128_pi.dwg *************

To create these drawings :
Load spiral_a.lsp (load "spiral_a")
Then from command line, type spiral_3
In response to the prompt message "How many rounds (def = 2 ) ?" Type in 1, 6 & 64 to get these pictures.

Go to Fun_Math Content Table Trisecting an Angle Special Curves

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006