Special Curves

Go to Fun_Math Content Table Trisecting an Angle Special Curves

Trisection using Special Curves

Trisectrix by Maclaurin

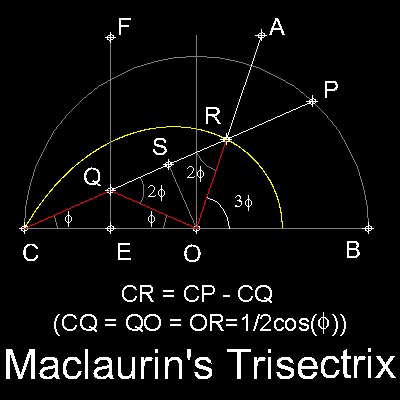
Colin Maclaurin (1698-1746) used a curve called "Trisectrix" to accomplish Angle Trisection.

His idea is shown in the figure shown below.

Equation of Trisectrix

In polar coordinate: r = CP - CQ = 2cos(q) - 1/2cos(q)

=(2cos2q)/(2cosq) + 1/(2cosq) = 2QS + CQ = CR.

Therefore QS = SR, and OQ = OR.

******** Maclaurin_tri_desc.dwg ********
In rectangular coordinate:

Assuming temporalily that point C is the origin of X-Y axis

by replacing r by sqrt(x² + y²) and cosq by y/sqrt(x² + y²)

y² = x²(3 - 2x) /(1 + 2x)

Now shifting the X-coordinate orign from C to O (distance of 1) (replacing x by x+1)

Trisectrix equation is :y² = (x + 1)²(2x - 1) /(3 + 2x)

Characteristics of of Trisectrix

This curve intersects Y -axis at x = -1 and 1/2, and as angle QCO approaches 90 degree, point R approaches line x = -3/2,both up and down.

Why this curve can be used for trisecting angle becomes clear when this figure is compared with the following drawing used in deriving Trisection equation.

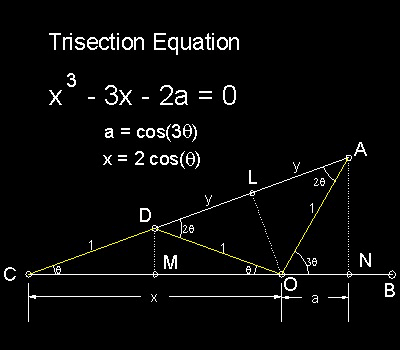
******** trisection_equation_desc.dwg ********

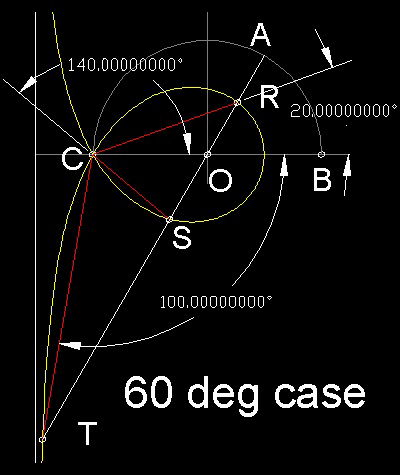
Example of Trisection-60 degree case

Angle AOB is to be trisected.

There are 3 trisection solutions.

They are one third of

given angle q (= 60) --->RCO = 20 deg

360 + q --->180 - OCS = 140 deg

2x360 + q --->RCT = 260 deg (shown as -100 deg).

You can see the process in animation.

******** Maclaurin_60_deg.dwg ********

To create this drawing and animation:
Load Maclaurin.lsp (load "Maclaurin")
Then from command line, type DRAW_MACLAURIN_ONLY for drawing Trisectrix curve

Trisection:

After drawing Trisectrix,define an anlge AOB to be trisected.

References

1. Dudley,Underwood :"The Trisectors" The Mathematical Association of America,1994.p 12-13

Go to Fun_Math Content Table Trisecting an Angle Special Curves

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006