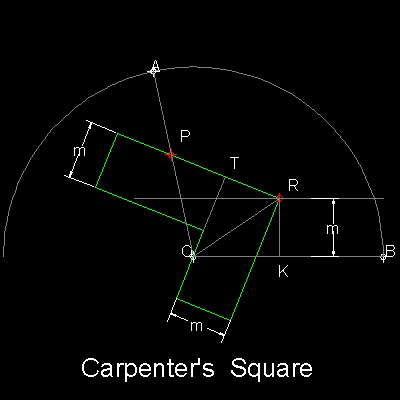
Carpenter's Square is shown in the figure shown below.

Angle to be trisected is AOB.
The width of the Carpenter's Square is m for both arms. While keeping the inside edge and the outside corner "R" passing through Point "o" and the line with distance m apart from line OB respectively, the trisection of angle AOB is done when a point "P" on the outside edge 2m from the point "R" passes through line AO.
Three triangles OPT, ORT and ORK are congruent.
You can see the process in animation.
******** carpenter's_square_desc.dwg ********
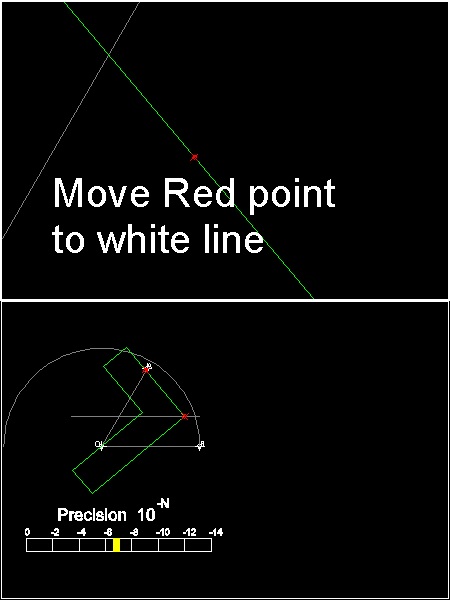
Top viewport: Cursor must be on this viewport. This viewport is zoomed up for moving cursor closer to the line angle is defined.
Bottom viewport: the global view with precision bar
********** carpenter_square_viewport.dwg **********
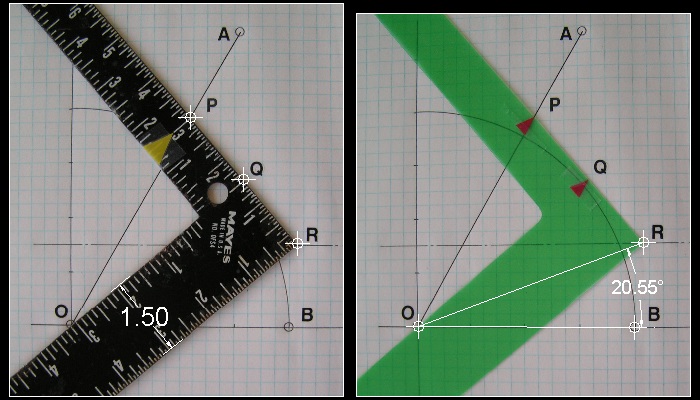
The Carpenter's Square in the author's garage was used in the actual test for trisecting 60 degrees angle. (shown in the left of the following picture.)
This ruler has different width for two legs, 1.0 and 1.5 inch.
Shown in the right is a copy of this ruler made of a transparent,film-like vinyl sheet used as separater in the binder.
*********************** carpenter's_square_model_12.dwg ***********************
To create this drawing and animation:
Load carp_square.lsp (load "carp_square")
Then from command line, type carpenter_square
For a quick look , type test & detail_test
Animation file creation: animation_carpsqr
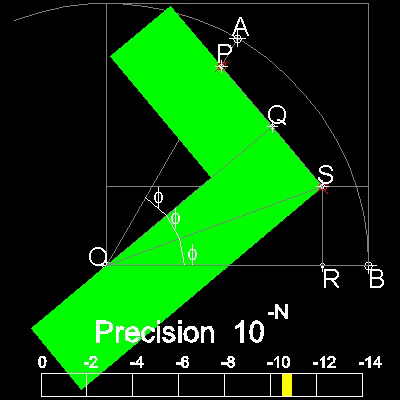
Input @6<60. for 60 degrees input
** carpenter's_square_60_deg_case.dwg **
1. Yates, Robert Carl : "The Trisection problem", p 36-37
2. Scudder, H.T. : How to trisect an Angle with a Carpenter's Square,American Mathematical Monthly,1928,pp.250-251
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.