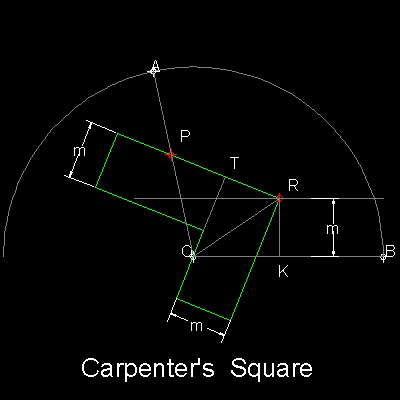
Carpenter's Square is shown in the figure shown below.

Angle to be trisected is AOB.
The width of the Carpenter's Square is m for both arms. While keeping the inside edge and the outside corner "R" passing through Point "O" and the line with distance m apart from line OB respectively, the trisection of angle AOB is done when a point "P" on the outside edge 2m from the point "R" passes through line AO.
Three triangles OPT, ORT and ORK are congruent.
You can see the process in animation.
For detail, go to the section Carpenter's Square.
****** carpenter's_square_desc.dwg ******
"Tomahawk" is shown in the figure shown below.
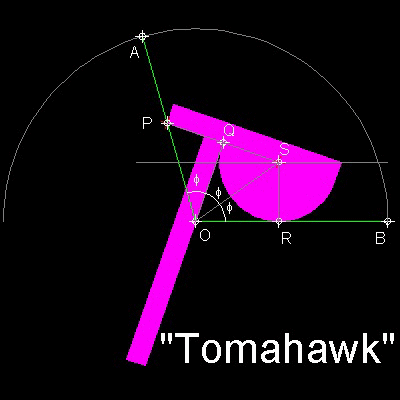
Tomahawk is made up of straight edge OQ, a semicircle SQR, and a sharp corner point "P" at a distance of the same radius from point "Q". The angle to be trisected is AOB.
The trisection is done when the point "P" passes through line AO while the inside edge OQ of the Tomahawk's handle being kept on the point "O". Just as in the case of Carpenter's Square, the following relation holds.
PQ = QS = SR
You can see the process in animation.
For detail, go to the section Tomahawk.
************** tomahawk_desc.dwg **************
Drafter's Triangles is shown in the figure shown below.
Two trangles CDE & LMN are the commonly used ones in drafting.
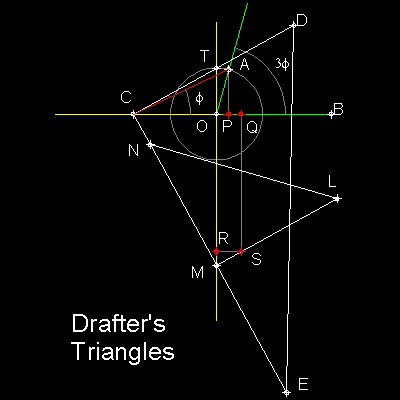
Draw a unit circle with center "O".
Define an angle to be trisected AOB,
with point "A" on this unit circle.
Angle AOP is 90 degrees
and length OP = cos(AOB)=a .
Point "Q" is (2a, 0)
Define a point "R" on y-axis such that
OR = 3 times radius of unit circle.
Define a point "S" such that RS = OQ = 2a
For detail, go to the section Drafter's Triangles.
********* drafter's_triangles_desc.dwg *********
Trisection procedure.
"C" stays on X-axis,and CD passes through the point "T"
The bases of the triangles CE and MN are on the same line.
The line LM passes through point "S"
Then when the corner point M comes on the y-axis, the trisection is done.
You can see the process in animation.
1. Robert C.Yates:"The Trisection problem"
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.