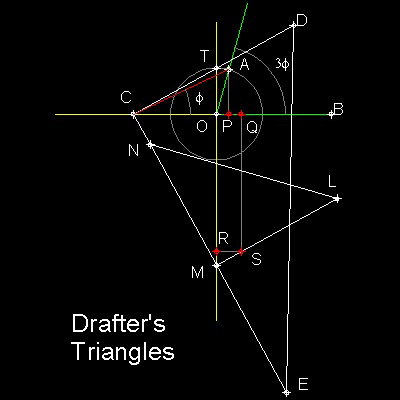
Drafter's Triangles is shown in the figure shown below.

Two trangles CDE & LMN are the commonly used ones in drafting.
Draw a unit circle with center "O".
Define an angle to be trisected AOB, with point "A" on this unit circle.
Angle AOP is 90 degrees and length OP = cos(AOB)=a .
Point "Q" is (2a, 0)
Define a point "R" on y-axis such that OR = 3 times radius of unit circle.
Define a point "S" such that RS = OQ = 2a
******** drafter's_triangles_desc.dwg ********
Trisection procedure.
"C" stays on X-axis,and CD passes through the point "T"
The bases of the triangles CE and MN are on the same line.
The line LM passes through point "S"
Then when the corner point M comes on the y-axis, the trisection is done.
You can see the process in animation
This is a picture of the actual operation. The radius of the circle is 2 inches, and the angle to be trisected is 60 degrees.
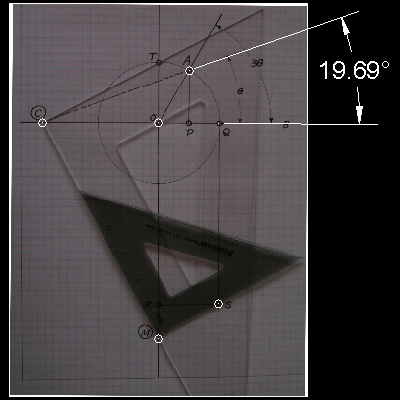
The author used a digital camera ,which stores image in JPG file(the file size is around 800 KB). The steps taken are:
1. Take a photo of the final position of triangles.
2. Transfer the file to my PC.
3. Open the file using "Insert"-> "Raster Image" option in AutoCAD.
4. Create points on the photo, and measure the resulting angle using "Dimension" -> "Angular" option.
5. In Command line window, type JPGOUT to save the result in JPG file.
******** triangles_example_60_deg.dwg ********
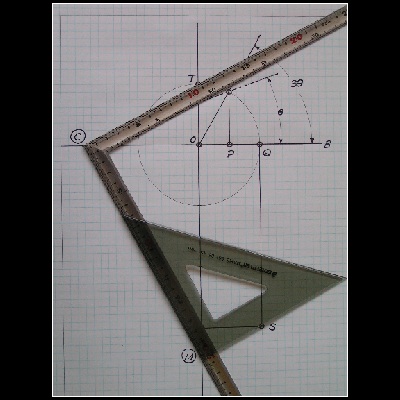
A 30-60 deg drafting triangle can be replaced by any right angled ruler.The author used a typical Japanese Carpenter's Square (Its width is about 1/2 inch).
******** triangles_example_60_deg_2.dwg ********
To create this drawing and animation:
Load triangle.lsp (load "triangle")
Then from command line, type triangle
For a quick look , type test_triangle
Animation file creation: animation_triangle
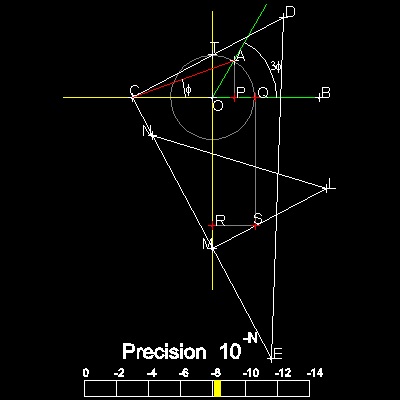
******** triangles_trisection_60_deg.dwg ********
1. Yates, Robert Carl : "The Trisection problem",pp. 43 - 44.
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.