包絡線 についての話題
このページにあるアニメーションのリスト（ハイパーテキストをクリックするとアニメーションがみられます。）
ここにもどるにはブラウザーの"Back" ボタンを使う。
1. 直線によって出来る包絡線としての円錐曲線
直線によって出来る包絡線としての円錐曲線
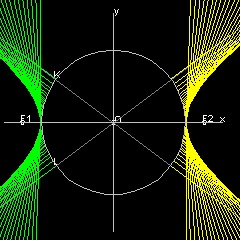
楕円 を描くアニメーション 放物線 を描くアニメーション 双曲線 を描くアニメーション
製図用直角三角定規で作る円錐曲線
楕円 を描くアニメーション 放物線 を描くアニメーション 双曲線 を描くアニメーション
折り紙で作る円錐曲線
楕円 を描くアニメーション 放物線 を描くアニメーション 双曲線 を描くアニメーション
詳細については, それぞれ 楕円 (Ellipse) , 放物線 (Parabola) , 双曲線 (Hyperbola) の項を参照されたい。
2. 直線によって出来る包絡線としてのサイクロイド、エピサイクロイド、ハイポサイクロイド
サイクロイド
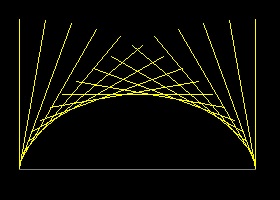
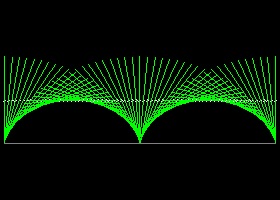
サイクロイド #0 アニメーション サイクロイド #1 アニメーション サイクロイド #2 アニメーション
詳細については, サイクロイド （Ｃｙｃｌｏｉｄ） を参照されたい。
エピサイクロイド
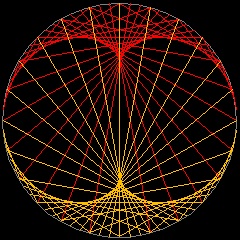
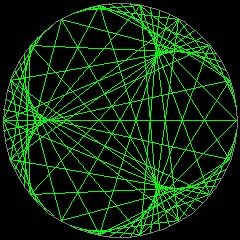
ハート形(Cardioid) のアニメーション ネフロイド(Nephroid) のアニメーション クレモナ(Cremona) のアニメーション
詳細については, エピサイクロイド(Epicycloid )を参照されたい。
ハイポサイクロイド
デルトイド(Deltoid) のアニメーション アストロイド(Astroid) のアニメーション 六角 ハイポサイクロイド のアニメーション
詳細については,
ハイポサイクロイド(Hypocycloid) を参照されたい。
内容の目次
- 1. 直線によって出来る包絡線としての円錐曲線
- 2. 直線によって出来る包絡線としてのサイクロイド、エピサイクロイド、ハイポサイクロイド
- 3. 直線によって出来る包絡線としての曲線
- 4. 円によって出来る包絡線としての曲線
- 5. 楕円によって出来る包絡線としての曲線
- 6. 放物線によって出来る包絡線としての曲線
- 7. 包絡線 および 垂足曲線 について
1. 直線によって出来る包絡線としての円錐曲線
円錐曲線(楕円、放物線、双曲線) は ギリシャの数学者 メナケムス(Menaechmus(about 380 BC - about 320 BC)) が ギリシャ三大問題の一つ "立方体の倍積問題" を 解くために考えだした二次曲線である。 彼はまたアレキサンダー大王の数学の教師でもあったことでも有名である。円錐曲線については 優れた 参考文献が 古来より数多く出版されているが、その中で 筆者が最近入手できたもの を参考文献の項に列挙した。 これ以外にも 多数あります。
1.1 楕円 (Ellipse)
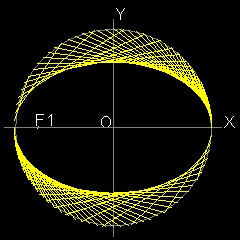
直線によって出来る包絡線
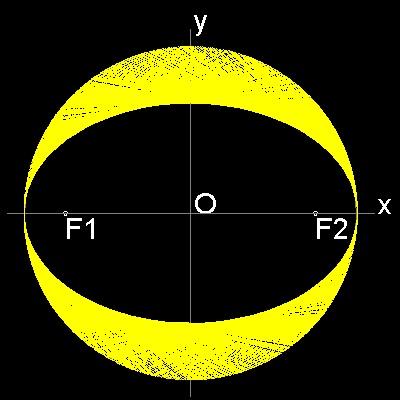
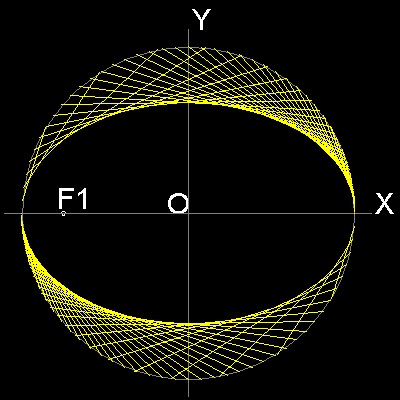
************* ellipse_manual_2.dwg *************
**************** ellipse_auto.dwg ****************
この図面とアニメーションの作成方法 :
プログラム conics_by_line.lsp をロードする。 (load "conics_by_line")
コマンド ラインから ellipse_auto と実行命令をタイプする。
ellipse_manual_2.dwg の図面を描くには, コマンド ラインから ellipse_manual_2 と 入力する。
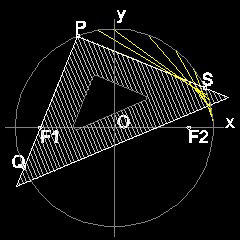
楕円の幾何学的特性
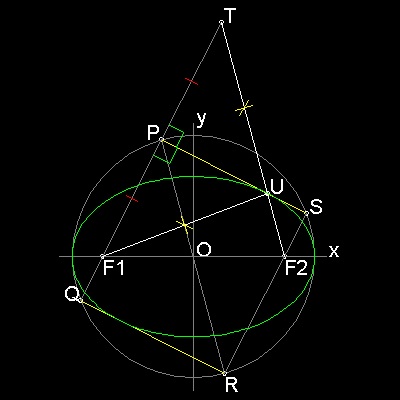
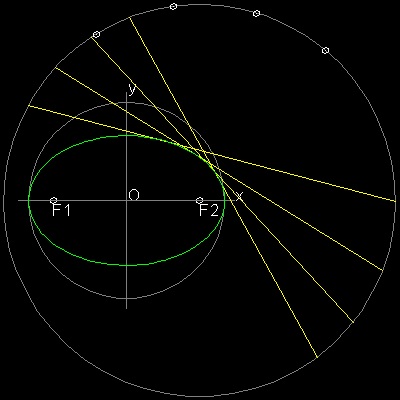
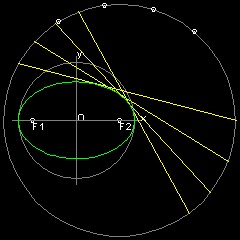
XY座標軸の原点 O を中心として半径 a の円を描く。 X軸上に点O から 距離c の点F1を選ぶ。 円上の点P からF1を通りもう一つの円上の点Qまで線を引く。 点PからPQに直角に直線PS を引く。 S は 円上の点である。 円上の４点を結び 長方形PQRS を作る。この時SR と Ｘ軸の交点をF2とする。 F1P を延長して F1P = PT となるように 点T を定める。 TF2 は PS と 点Uで交わる。 PQ は SR に平行であるから Δ OPF1 ≡ Δ ORF2 また Δ UPF1 ≡ Δ UPT であるから, F1U = UT そして ∠F1UP = ∠TUP = ∠SUF2 従って F2 = (c 0), そして UF1 + UF2 = UF2 + UT = PR = 2a (定数) つまり点U はF1, F2を焦点とする楕円上の点であるだけでなく ∠F1UP = ∠SUF2であるから この点で 楕円は線分PS と接している。 この様にして作られた線分(PS,QR)の集まりは 上の図のように 包絡線として 楕円を形成することがわかる。この図面の作成方法 :
プログラム conics_by_line.lsp をロードする。 (load "conics_by_line")
コマンド ラインから ellipse_model と実行命令をタイプする。
*************** ellipse_model.dwg ***************
製図用三角定規を使った作図
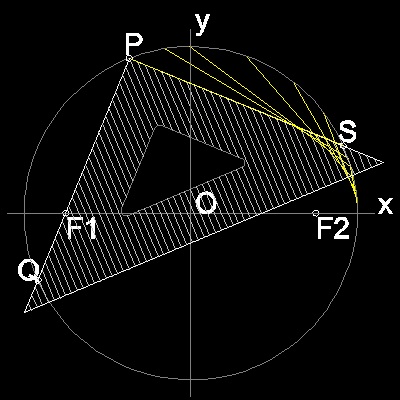上の図でP,Q,S は円周上の点であることから ∠SPQ は 直角である。
このことを利用すると 製図用三角定規を使って 包絡線を引くことが出来る。
直角の頂点を円周上に置き、直角を挟む一辺が焦点F1を通るようにする。
そのとき 直角を挟むもう一方の辺を使って線を引くとこれが 線分PS に相当する。
この図面とアニメーションの作成方法 :
プログラム conics_by_line.lsp をロードする。 (load "conics_by_line")
コマンド ラインから ellipse_by_triangle と実行命令をタイプする。
************ ellipse_by_triangle.dwg ************
折り紙による作図
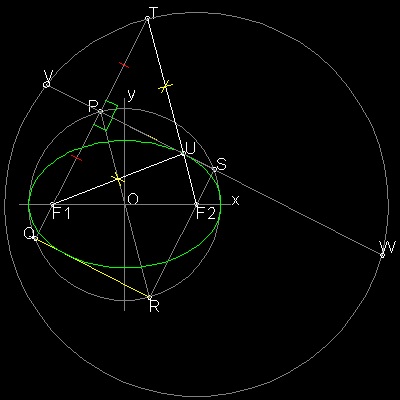点Tは焦点F2を中心にして半径が 2a の円周上にある。
PS を延長してこの外側の円との交点を V,W とすると VWは
F1T の垂直二等分線になっていることがわかる。
これを折り紙の言葉で表すと次のように言える。
この大きな円を円形の紙だと考える。円上の点 T を 焦点F1に
重なるように折るとその折り目がVWとなる。
つまり F2を中心として半径2a の円周上の点を F1に重なるように折ると
その折り目 VW の作る包絡線としてF1,F2を焦点とする楕円が得られる。
この図面の作成方法 :
プログラム conics_by_line.lsp をロードする。 (load "conics_by_line")
コマンド ラインから ellipse_model と実行命令をタイプする。
"Want to continue ?" と訊いてくるから "Yes" と答える。
************** ellipse_model_2.dwg **************
折り紙による作図の結果:
この図面とアニメーションの作成方法 :
プログラム conics_by_line.lsp をロードする。 (load "conics_by_line")
コマンド ラインから ellipse_by_folding と実行命令をタイプする。
************* ellipse_by_folding.dwg *************
1.2 放物線 (Parabola)
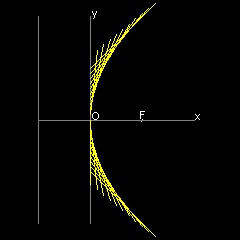
直線によって出来る包絡線
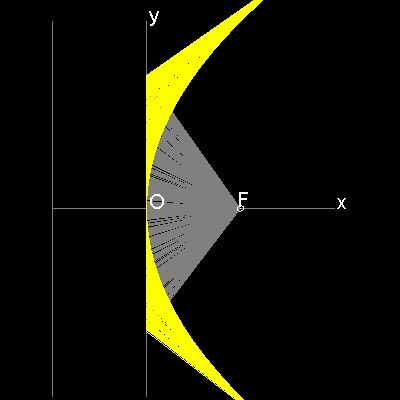
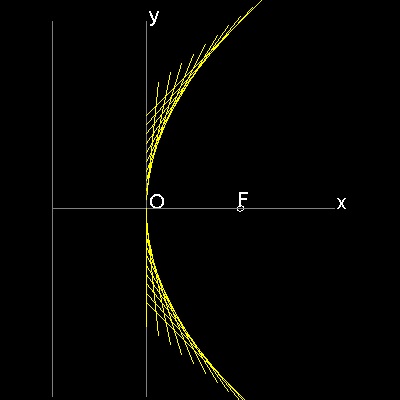
************* parabola_manual_2.dwg *************
**************** parabola_line.dwg ****************
この図面とアニメーションの作成方法 :
プログラム conics_by_line.lsp をロードする。 (load "conics_by_line")
コマンド ラインから parabola_auto と実行命令をタイプする。
ellipse_manual_2.dwg の図面をつくるには, コマンド ラインから ellipse_manual_2 と実行命令をタイプする。
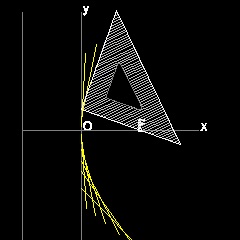
放物線の幾何学的特性
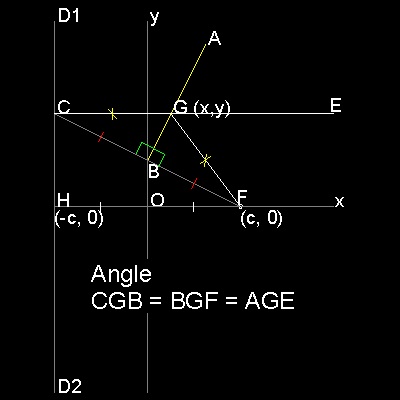
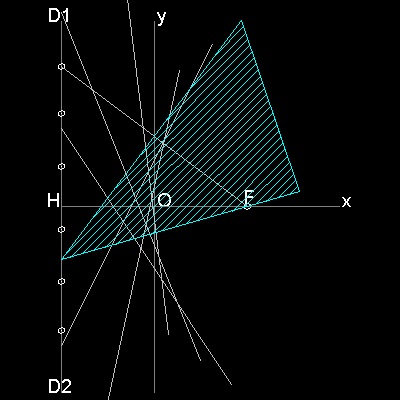
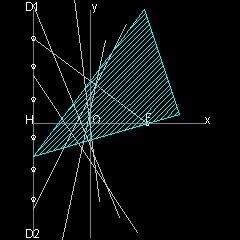
F は焦点 (c, 0), で Y 軸に平行で 原点から c の距離にある 直線 D1 D2は Directrix である。 Y 軸上の任意の点を B とする。FB は この directrix と C で交わる。 点B で FC に垂直にABを引く。 点C からX-軸に平行線を引くと AB と点Gで交わる。 すると GC = GF となる。 これは 放物線の定義である。 更に ∠CGB = ∠BGF = ∠AGE であるから ∠EGF の二等分線はABに垂直である。 従って 点Gは放物線上の点であるだけでなく AB はこの点で放物線に接している。 故に AB のような線分の包絡線は放物線を形成する。
この図面の作成方法 :
プログラム conics_by_line.lsp をロードする。 (load "conics_by_line")
コマンド ラインから parabola_model と実行命令をタイプする。
放物線の定義 GC = GF から 放物線の方程式を導く。
GC2 = GF2
であるから
GC = (x + c) ,GF = {(x-c)2 + y2}1/2
を代入して 項をまとめると
y2 = 4cx
が得られる。
*************** parabola_model.dwg ***************
製図用三角定規を使った作図
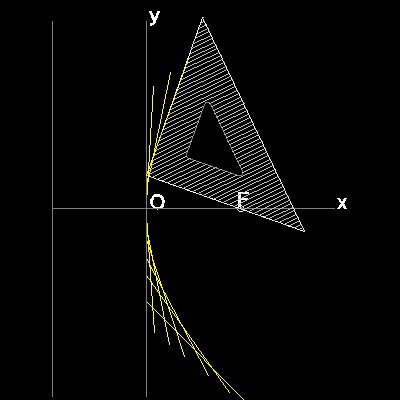上の説明図で 点A,B,Fを結ぶと ∠ABF は直角であるからこの三角形を
製図用三角定規で置き換えて考えることが出来る。
すなわち 直角を挟む一辺が 焦点を通るようにしながら
直角の頂点は Y-軸上を動くようにすると 直角を挟む
もう一つの辺が包絡線の一部となる。
この図面とアニメーションの作成方法 :
プログラム conics_by_line.lsp をロードする。 (load "conics_by_line")
コマンド ラインから parabola_by_triangle と実行命令をタイプする。
************ parabola_by_triangle.dwg ************
折り紙による作図
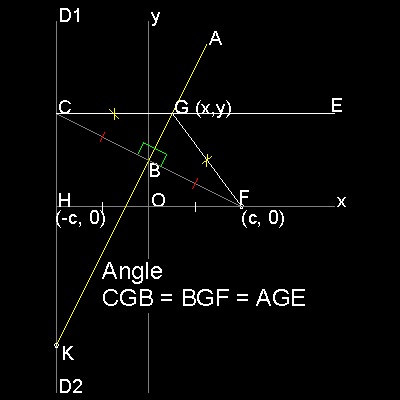左の図で点G はCFの垂直二等分線AK 上にある。
この図全体が一枚の紙であると考えると
AK は線分D1 D2上の点C が焦点F
に重なるように紙を折った時にできる折り目線であると考えられる。
注記: directrix D1 D2 はその中心が X-軸上の無限遠に位置する 円弧であると 考えられる。
この図面の作成方法 :
プログラム conics_by_line.lsp をロードする。 (load "conics_by_line")
コマンド ラインから parabola_model と実行命令をタイプする。
実行が終了してから 線分 BK を追加する。
************** parabola_model_2.dwg **************
折り紙による作図の結果:
この図面とアニメーションの作成方法 :
プログラム conics_by_line.lsp をロードする。 (load "conics_by_line")
コマンド ラインから parabola_by_folding と実行命令をタイプする。
************* parabola_by_folding.dwg *************
1.3 双曲線 (Hyperbola)
直線によって出来る包絡線
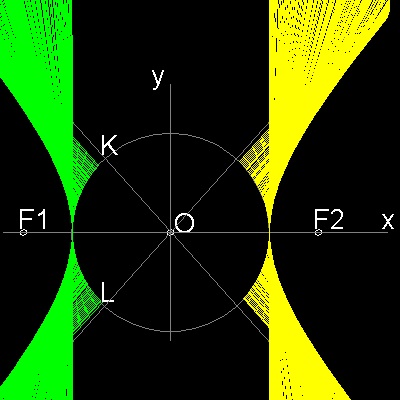
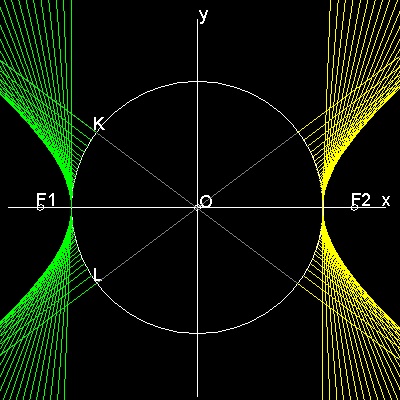
*********** hyperbola_manual_2.dwg ***********
************** hyperbola_auto.dwg **************
この図面とアニメーションの作成方法 :
プログラム conics_by_line.lsp をロードする。 (load "conics_by_line")
コマンド ラインから hyperbola_auto と実行命令をタイプする。
hyperbola_manual_2.dwg の図面をつくるには, コマンド ラインから hyperbola_manual_2 と実行命令をタイプする。
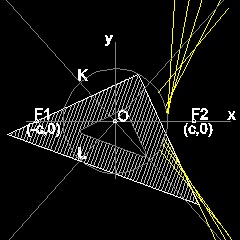
双曲線の幾何学的特性
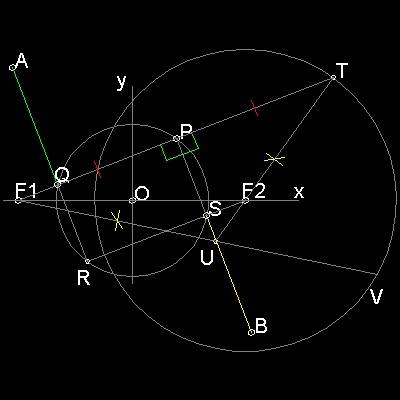
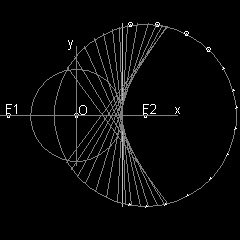
座標軸の原点を中心にして半径 a の円を描く。 X-軸上でこの円の外側こ、中心から c の距離に二つの点 F1,F2 を定める。(c > a) 円上の一点P をF1と直線で結び、円との交点をQとする。 二点P,Q で 線分PQに垂線を立てると その延長は 円と それぞれS,R で交わり PQRS は長方形になる。 また 対称性により RS は X-軸と点F2で交わる。 F1P をP の方向に延長して F1P = PT となるように 点T を決める。 TをF2と結ぶと、延長線が PS と 点 U で交わる。 Δ UPF1 ≡ Δ UPT であるから F1U = UT , UF1 - UF2 = UT - UF2 = F2T = PR = 2a (定数). 従って 点 U は F1,F2 を焦点とする 双曲線上にある。 更に ∠ PUF1 = ∠ PUT =∠ BUV であるから 線分 BP は 点 U でこの双曲線に接していることがわかる。
この図面の作成方法 :
プログラム conics_by_line.lsp をロードする。 (load "conics_by_line")
コマンド ラインから hyperbola_model と実行命令をタイプする。
************* hyperbola_model.dwg *************
製図用三角定規を使った作図
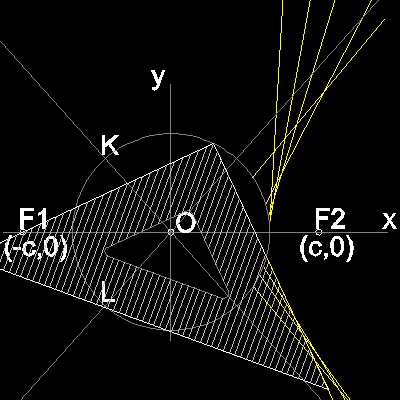四点 P,Q,R, S が中心の円周上にあり ∠SPQ は直角である。
この性質を利用すると、製図用三角定規を使って双曲線を
線分の包絡線としてつくることができる。
直角を挟む一辺が常にF1を通るように拘束しながら
直角の頂点を円周上で動かしたとき
直角を挟む他の辺が作る包絡線が 双曲線である。
この図面とアニメーションの作成方法 :
プログラム conics_by_line.lsp をロードする。 (load "conics_by_line")
コマンド ラインから hyperbola_by_triangle と実行命令をタイプする。
************ hyperbola_by_triangle.dwg ************
折り紙による作図
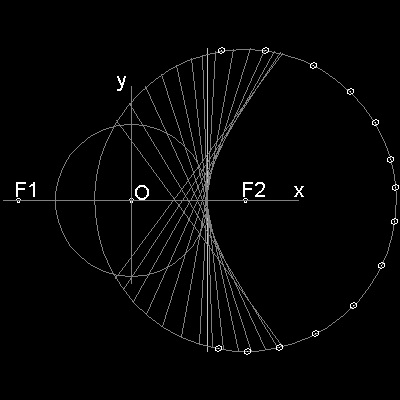焦点F2 を中心として半径 2a の円周上にある点Tと
もう一つの焦点F1は
包絡線を作る線分PBに関して
線対称の位置にある。
従って この図全体が一枚の紙であると考えたとき
T をつかんでF1に重なるように紙を折ると
折り目線として PBが残る。
それを円周上の幾つかの点に対して行うと
折り目の包絡線として 双曲線が得られる。
この図面とアニメーションの作成方法 :
プログラム conics_by_line.lsp をロードする。 (load "conics_by_line")
コマンド ラインから hyperbola_by_folding と実行命令をタイプする。
********** hyperbola_by_folding.dwg **********
2. 直線によって出来る包絡線としてのサイクロイド、エピサイクロイド、ハイポサイクロイド
サイクロイド(Cycloid)は 円が直線上を滑ることなく回転しながら動くとき、その円周上の点の軌跡である。ここで 直線を円で置き換えた場合を考える。
運動する円の周上の点の軌跡は 、回転運動する領域(内側か 外側か）によって
外側の場合: エピサイクロイド (Epi-cycloid)
内側の場合: ハイポサイクロイド (Hypo-cycloid)
と言う名前で呼ばれている。
2.1 サイクロイド (Cycloid)
直線によって出来る包絡線
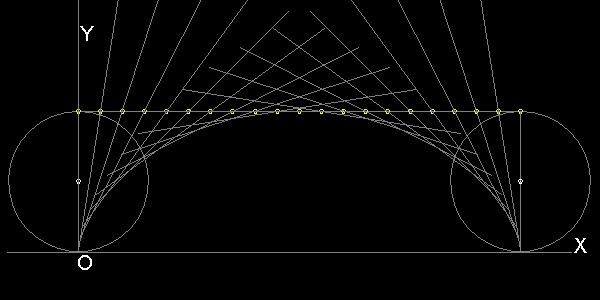(1) 円の直径 (2a)の 高さに
長さが2aπ の線分を引く。
(2) これを ｎ等分(ここでは n = 20)する。
(3) まず左端で X 軸に垂直な
線分を立てる。
(4) 右に一点進む度にこの垂直線分を
時計回転方向に
(2π/n) ラジアン 回転させる。
******************* cycloid_by_line_envelope.dwg ************************
(1) 直径 4a の円の直径が 点OでX 軸に
垂直になるように置く。
(2) この円を回転させて右に動かす時に、
直径の線分も一緒に動かすと
図のような包絡線が出来て、
これが サイクロイドになっている。
******************* cycloid_by_line_envelope_2.dwg *********************
この図面とアニメーションの作成方法 :
プログラム cycloid1.lsp をロードする。 (load "cycloid1")
コマンド ラインから draw_cycloid_by_line と実行命令をタイプする。
一番目の例: 分割の数 = 20
二番目の例: 分割の数 = 200, 名前 が layer2の画層 (黄色の点) は非表示に設定してある。
サイクロイド( Cycloid )の幾何学的特性
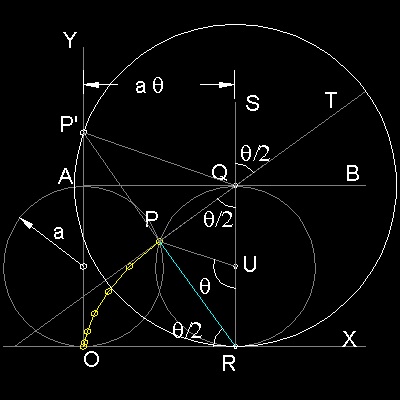
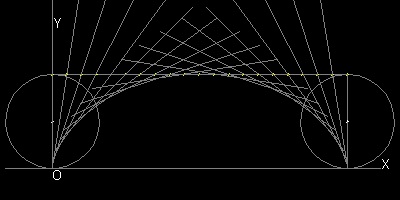
半径 "a" の円周上の一点P が最初はX-軸上の原点にあるとする。 この円が線分OX上を摩擦なしに角度 θ(ラジアン)回転して右に進んだとする。 その時点での円の頂点、中心、X-軸と接する点を それぞれQ,R,U とする。 ∠RPQ は直角で、点Rがこの時点での回転中心になっており、線分PQ(及び PT) は点Pの軌跡が作る曲線に接している。 更に ∠PUR = θ, ∠PRO = ∠PQR = ∠SQT = θ/2 であるから OR = a θ. 従って 点P(x,y) は θ をパラメターとして次の様に表せる。 x = a(θ - sin θ) y = 2a(1 - cosθ) "PT" のような線分は 上に示すようにサイクロイドの包絡線になる。 サイクロイドの包絡線の作り方： (1) X-軸に平行で 長さが2πa の線分AB を引き、それを n 等分する。 点AでABに垂直な長さが2aの線を引く 右側の次の点に行く度に角度を2π/n だけ時計回り方向に増加させながら 線を引いていく。 (2) 半径 が 2a の円 を描き、その直径が 原点で垂直になるようにする。 この大きな円をX軸上に転がすと その直径の作る包絡線が サイクロイドになる。 その理由は 大きな円が 点 R にきたとき, ∠RQP' = θ であり PT がその直径の一部になっている。
*************** cycloid_model.dwg ***************
この図面の作成方法 :
プログラム cycloid1.lsp をロードする。 (load "cycloid1")
コマンド ラインから draw_cycloid_model と実行命令をタイプする。
分割数を 20 に選び、７番目で 実行を中止した後、手作業で図面に修正を加える。
2.2 エピサイクロイド(Epicycloid)
エピサイクロイド の例
静止している円の半径 = a運動する円の半径 = b
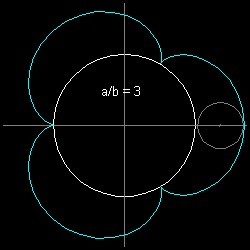
とすると a/b の比の値によって異なる形の図形が得られ a/b の比が 1,2 3 の時
その図形には特別な名前が付けられている。
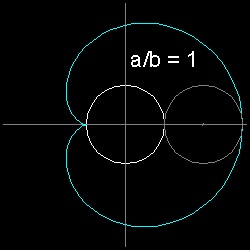
a/b = 1-----ハート形(Cardioid) 語源はギリシャ語で kerdia(心臓) + eidos(形、見かけ)--->心臓の形をした図形
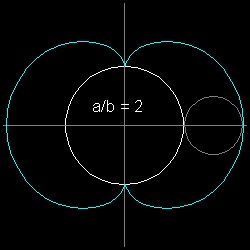
a/b = 2-----ネフロイド(Nephroid) 語源はギリシャ語で nephros(腎臓) + eidos(形、見かけ)--->腎臓の形をした図形
a/b = 3-----クレモナ(Cremona) イタリアの数学者 クレモナ（Luigi Cremona)(1830-1903)の名前に由来する。
**** epicycloid_cardioid.dwg
**** **** epicycloid_nephroid.dwg
**** **** epicycloid_cremona.dwg****
** ハート形のアニメーションを見る ** ネフロイドのアニメーションを見る ** クレモナのアニメーションを見る
この図面とアニメーションの作成方法 :
プログラム draw_epicycloid.lsp をロードする。 (load "draw_epicycloid")
コマンド ラインから draw_epicycloid_auto と実行命令をタイプする。
入力の既定値は a = 1, b = 1, 一周の分割数 = 72 に設定してあるから
ハート形の場合: 総て 既定値を使うので "Enter" キーを押すだけ。
ネフロイド(Nephroid)の場合: a = 2 であとは 既定値を使うので "Enter" キーを押すだけ。
クレモナ(Cremona)の場合: a = 3 であとは 既定値を使うので "Enter" キーを押すだけ。
エピサイクロイド の幾何学特性
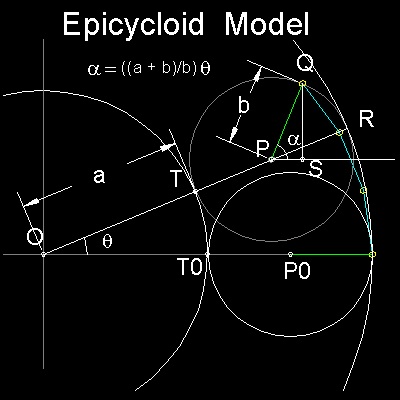
原点 Oを中心として半径a の円の周りを半径b の円
(中心Pの始点をPOとする)が動くときの
動円上の点の軌跡は次のようになる。
動円の中心がPにきた時 OP がX軸となす角をθ とすると
そこに来るまでに 動いた弧の距離は (a + b)θ であるから
動円が回転した角度を α とすると
b α = (a + b)θ
である。
従って α = {(a + b)/b} θ
その結果 エピサイクロイド 上の点Q(x,y)
は次のような式で書き表される。
x = (a + b)cosθ + b cos α
y = (a + b)sinθ + b sin α
ここで α = {(a + b)/b} θ
例(1):ハート形 (a = b)
x = a{2cosθ + cos2θ}
y = a{2sinθ + sin2θ}
例(2):ネフロイド (a = 2b)
x = b{3cosθ + cos3θ}
y = b{3sinθ + sin3θ}
************* epicycloid_model.dwg *************
この図面の作成方法 :
プログラム draw_epicycloid.lsp をロードする。 (load "draw_epicycloid")
コマンド ラインから epicycloid_model と実行命令をタイプする。
(入力データ) 内側の円の半径= 2, 外側の円の半径= 1, に設定して、 一周を 72 分割にする。
実行終了後、 図面に修正を加える。
ストリング アートとしてのエピサイクロイド (Curve Stitching)
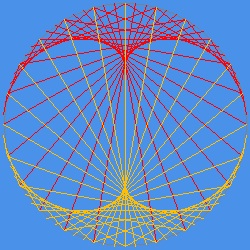
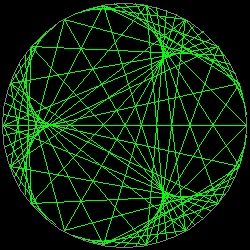
円周を何等分かして、その上の二点をある規則に従って次々と線で結ぶとその包絡線がエピサイクロイドになることが知られている。 この線を色のついた糸で置き換えたものが "Curve Stitching" と呼ばれる
ストリング アート である。 その例を下に示す。
円周の分割数、 糸 および 背景の色の組み合わせにより 思いもかけなかった、美しい結果が得られる。
(参考 3 )には "Curve Stitching" のテクニック、作品例、背景にある数理の説明についての解説 が掲載されている。
**** string_cardioid.dwg****
**** string_nephroid.dwg****
**** string_cremona.dwg****
** ハート形のアニメーションを見る ** ネフロイドのアニメーションを見る ** クレモナのアニメーションを見る
この図面とアニメーションの作成方法 :
プログラム string_epicycloid.lsp をロードする。 (load "string_epicycloid")
コマンド ラインから string_epicycloid と実行命令をタイプする。
入力の既定値は カスプの数 = 1, 一周の分割数 = 72 に設定してあるから
ハート形の場合: 総て 既定値を使うので "Enter" キーを押すだけ。
ネフロイド(Nephroid)の場合: a = 2 であとは 既定値を使うので "Enter" キーを押すだけ。
クレモナ(Cremona)の場合: a = 3 であとは 既定値を使うので "Enter" キーを押すだけ。
一本の線を引いて、次の線を引くまでの時間は 自動的に 7200 を 一周の分割数
で割り算した値に設定されている。 例えば 一周の分割数=72 のときは 100 ms(mil1i second)
7200/72 ms = 100 ms, つまり 100/1000 秒 = 1/10 秒 である。
エピサイクロイド を作る線の引き方
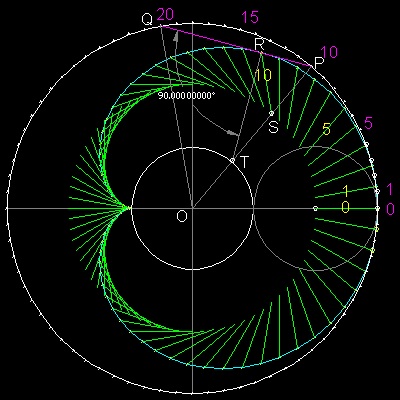
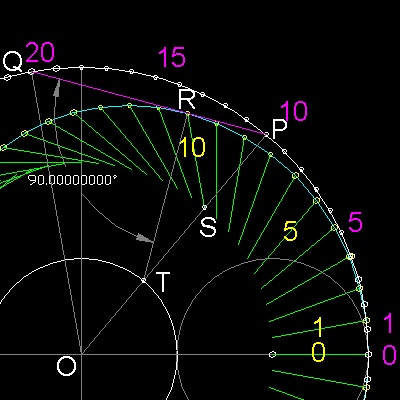
************ string_cardioid_model.dwg ************
******************* 部分拡大図 *******************
この図面の作成方法 :
プログラム draw_epicycloid.lsp をロードする。 (load "draw_epicycloid")
コマンド ラインから epicycloid_model と実行命令をタイプする。
(入力データ) 内側の円の半径= 1, 外側の円の半径= 1, に設定して、 一周を 72 分割にする。
実行終了後、 図面に修正を加える。
先ず包絡線を作る過程を説明して、その後それが確かに包絡線であることの証明をしよう。
例として ハート形を選ぶ。
1. 円周を N 等分して各点に図のように 0 から 順番に1,2,3,...(赤紫色で示す) と番号をつける。 ここでは N = 72
2. 始める点の番号を Mとする。
3. #M の点と #2M の点を結ぶ。 次に#2M の点と #4M の点を結ぶ。 次に#4M の点と #8M の点を結ぶ。 .....
(例)--- #1 の点から始める。 #1-- #2-- #4-- #8-- #16-- #32-- #64 と結ぶ。
次は #3-- #6-- #12-- #24-- #48-- と結ぶ。
次は #5-- #10-- #20-- #40-- と結ぶ。
次は #7-- #14-- #28-- #56-- と結ぶ。
ではこれが包絡線としてハート形になっていることを証明しよう。
上記の "" .... #10-- #20-- と結ぶ。" に 注目しよう。 #10, #20 の 点をそれぞれ P,Q とする。静止円の中心点 O と P を結ぶ直線は 静止円と T で交わり PT の中点 S は動円が T に接しているときの円の中心で あるから TS = SP である。 このときの動円上の点 R が 線分PQ 上にあり PR : RQ = 1 : 2 であり しかも ∠PRT が直角であることをしめす。 先ず OP が X 軸となす角を θ とする。 点 P, Q ,R の座標は次のようになる。 P: Px = 3a cos θ Py = 3s sin θ Q: Qx = 3a cos 2θ Qy = 3s sin 2θ R; Rx = a(2cos θ + cos 2θ) Rx = a(2sin θ + sin 2θ) 線分PQ を 1:2 に内分する点の座標を求めると x = (1/3)(Px + 2Qx)= Rx y = (1/3)(Py + 2Qy)= Ry となり この点は R に他ならないことがわかる。 また R は PT を直径とする円周上の点であるから ∠PRT は 直角である。
以上のことから R はハート形の曲線上にあり 、そのときの回転中心点 T に対し PQは
直角に動くからPQ はこの曲線にこの点で接線となっている。
故に 以上の規則に従う線分の集まりは ハート形の包絡線を形成することがわかる。
ネフロイドの場合 : ハート形との違いは次の部分である。
3. #M の点と #2M の点を結ぶ。 次に#2M の点と #4M の点を結ぶ。 次に#4M の点と #8M の点を結ぶ。 .....
これが
3. #M の点と #3M の点を結ぶ。 次に#3M の点と #9M の点を結ぶ。 .....
となる。
例えば 下の図で #5 と #15 を結ぶ。
それと PR : RQ = 1 : 2 が PR : RQ = 1 : 3 になる。
QO が RS と平行であることにも注目されたい。
ここまでくれば クレモナの場合に どうなるかは推測できるであろう。
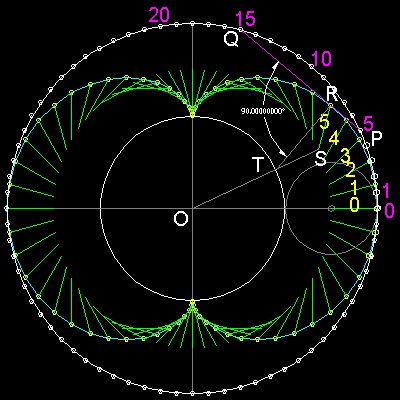
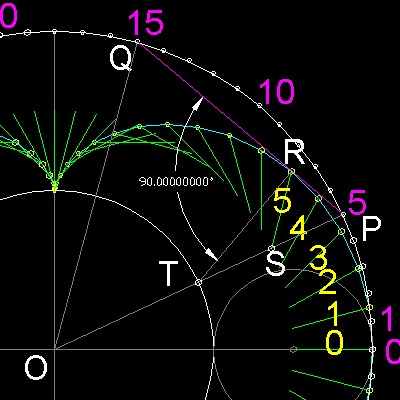
************ string_nephroid_model.dwg ************
******************* 部分拡大図 *******************
この図面の作成方法 :
プログラム draw_epicycloid.lsp をロードする。 (load "draw_epicycloid")
コマンド ラインから epicycloid_model と実行命令をタイプする。
(入力データ) 内側の円の半径= 2, 外側の円の半径= 1, に設定して、 一周を 72 分割にする。
実行終了後、 図面に修正を加える。
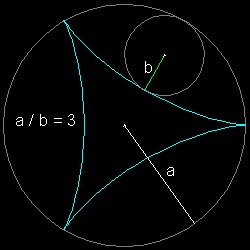
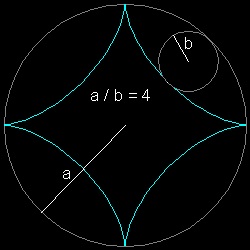
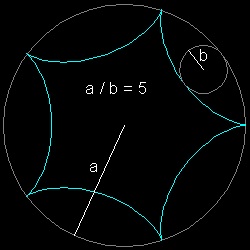
2.3 ハイポサイクロイド (Hypo-cycloid)
ハイポサイクロイド の例
静止している円の半径 = a運動する円の半径 = b
とすると a/b の比の値によって異なる形の図形が得られ a/b の比が 3,4 の時
その図形には特別な名前が付けられている。
a/b = 3-----デルタ形(Deltoid) 語源はギリシャ語のアルファベット Δ + eidos(形、見かけ)--->Δの形をした図形
a/b = 4-----星芒形(Atroid) 語源はギリシャ語で aster(星) + eidos(形、見かけ)--->星の形をした図形
******* deltoid_curve.dwg
******* ****** astroid_curve.dwg
****** ******* 5_cusp_curve.dwg*******
** デルタ形のアニメーションを見る ** 星芒形のアニメーションを見る ** ５カスプのアニメーションを見る
この図面とアニメーションの作成方法 :
プログラム draw_hypocycloid.lsp をロードする。 (load "draw_hypocycloid")
コマンド ラインから draw_hypocycloid_auto と実行命令をタイプする。
入力の既定値は a = 3, b = 1, 一周の分割数 = 72 に設定してあるから
デルタ形の場合: 総て 既定値を使うので "Enter" キーを押すだけ。
星芒形の場合: a = 4 であとは 既定値を使うので "Enter" キーを押すだけ。
５カスプの場合: a = 5 であとは 既定値を使うので "Enter" キーを押すだけ。
ハイポサイクロイド の幾何学特性
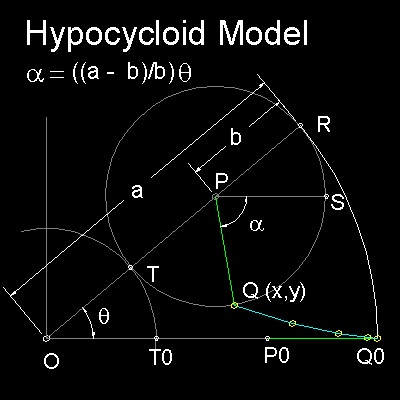
原点 Oを中心として半径a の円の内側に沿って 半径b の円
(中心Pの始点をPOとする)が動くときの
動円上の点の軌跡は次のようになる。
動円の中心がPにきた時 OP がX軸となす角をθ とすると
そこに来るまでに 動いた弧の距離は (a - b)θ であるから
動円が回転した角度を α とすると
b α = (a - b)θ
である。
従って α = {(a - b)/b} θ
その結果 ハイポサイクロイド 上の点Q(x,y)
は次のような式で書き表される。
x = (a - b)cosθ + b cos α
y = (a - b)sinθ - b sin α
ここで α = {(a - b)/b} θ
例(1):デルタ形 (a = 3b)
x = b{2cosθ + cos2θ}
y = b{2sinθ - sin2θ}
例(2):アストロイド (a = 4b)
x = b{3cosθ + cos3θ} = a(cosθ)3
y = b{3sinθ - sin3θ} = a(sinθ)3
(cosθ)2 + (sinθ)2 = 1 を使って θ を
取り除くと アストロイド が次のような式で表される。
X(2/3) + Y(2/3) = a(2/3)
************* hypocycloid_model.dwg *************
この図面の作成方法 :
プログラム draw_hypocycloid.lsp をロードする。 (load "draw_hypocycloid")
コマンド ラインから hypocycloid_model と実行命令をタイプする。
(入力データ) 外側の円の半径= 3, 内側の円の半径= 1, に設定して、 一周を 72 分割にする。
実行終了後、 図面に修正を加える。
ストリング アートとしてのハイポサイクロイド (Curve Stitching)(参考 3 )
円周を何等分かして、その上の二点をある規則に従って次々と線で結ぶとその包絡線がハイポサイクロイドになることが知られている。 この線を色のついた糸で置き換えたものが "Curve Stitching" と呼ばれる
ストリング アート である。 その例を下に示す。
****** string_deltoid.dwg
****** ***** string_astroid_1.dwg
***** *** string_hypocycloid_6.dwg ***
デルトイド-Deltoid のアニメーション アストロイド-Astroid のアニメーション 六角ハイポサイクロイドのアニメーション
この図面とアニメーションの作成方法 :
プログラム string_hypocycloid.lsp をロードする。 (load "string_hypocycloid")
コマンド ラインから string_hypocycloid と実行命令をタイプする。
入力の既定値は カスプの数 = 3, 一周の分割数 = 36 に設定してあるから
デルトイドの場合: 総て 既定値を使うので "Enter" キーを押すだけ。
アストロイドの場合: a = 4 であとは 既定値を使うので "Enter" キーを押すだけ。
六角 ハイポサイクロイド: a = 6 であとは 既定値を使うので "Enter" キーを押すだけ。
一本の線を引いて、次の線を引くまでの時間は 自動的に 7200 を 一周の分割数
で割り算した値に設定されている。 例えば 一周の分割数=72 のときは 100 ms(mil1i second)
7200/72 ms = 100 ms, つまり 100/1000 秒 = 1/10 秒 である。
ハイポサイクロイド を作る線の引き方
************* string_deltoid_model.dwg *************
********* string_deltoid_one_cusp.dwg *********
この図面の作成方法 :
プログラム string_hypocycloid.lsp をロードする。 (load "string_hypocycloid")
*** string_deltoid_model.dwg の場合：
コマンド ラインから string_hypocycloid_model と実行命令をタイプする。
(入力データ) 外側の円の半径= 3, 外側の円の半径= 1, に設定して、 一周を 36 分割にする。
実行終了後、 図面に修正を加える。
*** string_deltoid_one_cusp.dwg の場合:
コマンド ラインから string_one_cusp と実行命令をタイプする。
(入力データ) 外側の円の半径= 3, 外側の円の半径= 1, に設定して、 一周を 36 分割にする。
実行終了後、 図面に修正を加える。
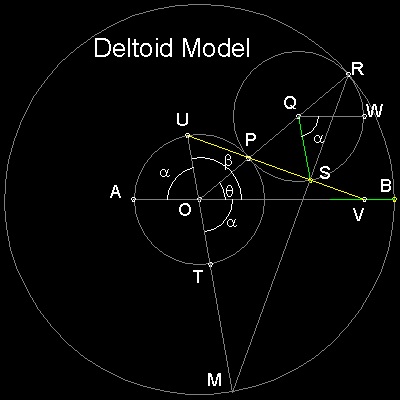
先ず包絡線を作る過程を説明して、その後それが確かに包絡線であることの証明をしよう。
例として デルトイドを選ぶ。
1. 中心が点 O で半径が (a-2b) の円を描く。
2. この円周上に X 軸から 角度 θ の点を P, AO から αの点を U とする。
3. UPの延長と OB の交点を V とする。 UV を結ぶ。
4. X 軸に対称な 下の円周にも同様な線を引く。
5. これを (θ + α) が 180° になるまで繰り返す。
6. これで 一個のカスプが 出来上がったので これを 点O のまわりに 回転 コピーすると
デルトイド が出来る。
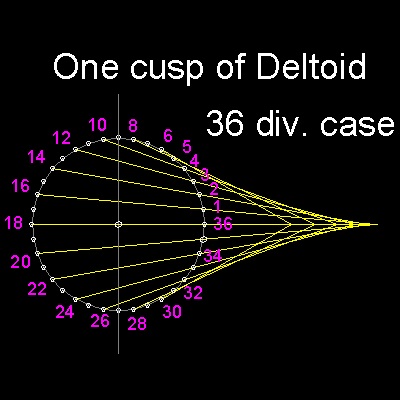
実例を上の右図に示した。
ここでは (a - 2b) の円を ３６ 等分 している。
便宜上、円周上の 点に 図のような番号付けをする。
#1 - #16, #2 - #14, #3 - #12, #4 - #10, #5 - #8 と順番に線をひく。
更に #35 - #20, #34 - #22, #33 - #24, #32 - #26, #30 - #28 と結ぶ。
この場合のように 最後の #6, #29 は点が一つしかない時は 円の中心と結ぶ線に
直角の線を引き それと OB との交点を求める。
包絡線であることの証明。
先ず OP が X 軸となす角を θ とする。
点 R , M の座標は次のようになる。
R: Rx = a cos θ Ry = a sin θ
M: Mx = a cos 2θ My = -a sin 2θ
線分PQ を 1:2 に内分する点の座標を求めると
x = (a/3)(2Rx + Mx)= (a/3){2 cos θ + cos 2θ}
y = (a/3)(2Ry + My)= (a/3){2 sin θ - sin 2θ}
となり この点は デルトイド上にある 点 S に他ならないことがわかる。
QP = QS = QR であるから ∠RSP は 直角である。
また R は 動円の回転中心であるから UV は デルトイドの接線になっている。
従って UV の 集合は デルトイド の包絡線である。
More on Epi and Hypo cycloids
接続する糸を例えば ３６等分して それぞれに異なる色をつけた特別な糸で置き換えると興味ある結果が得られる。更に 例えば ハート形の場合には ３分の１の点が ハート形の曲線の接線になっていることを利用すると １２番目の色が
ハート形を形成するので その部分を表に出すと 曲線がより鮮明に理解できる。 そのような処理をした結果を以下にしめす。
最初は 通常の線（３６色）を５７６本使用している。
もう一つのケースは 太めの線を ２８８本使ったものである。
| cardioid_36_576.dwg cardioid_36_576.jpg Cardioid  |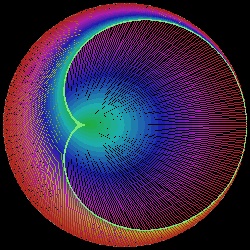
nephroid_36_576.dwg nephroid_36_576.jpg Nephroid  |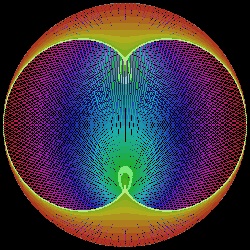
cremona_36_576.dwg cremona_36_576.jpg Cremona  |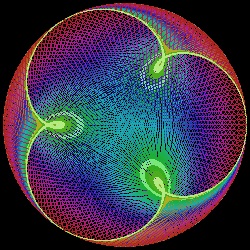
| cardioid_36_288_wide.dwg cardioid_36_288_wide.jpg Cardioid  |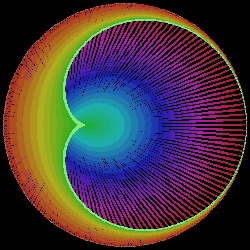
nephroid_36_288_wide.dwg nephroid_36_288_wide.jpg Nephroid  |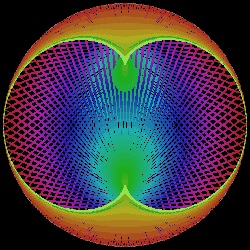
cremona_36_288_wide.dwg cremona_36_288_wide.jpg Cremona  |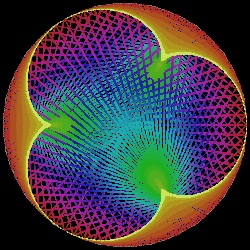
この図面の作成方法 :
プログラム string_hypocycloid.lsp をロードする。 (load "string_hypocycloid")
コマンド ラインから test_hypocycloid と実行命令をタイプする。
(入力データ) カスプの数を入力する。
使用する 多色線 の名称を入力する。 (例: string_36, wide_string_36)
実行終了後、 図面に修正を加える。
コマンド ラインから enhance_boundary と実行命令をタイプする。
エピサイクロイド、 ハイポサイクロイド、の 一般化
[18]は エピサイクロイド、 ハイポサイクロイド、を一般化して 説明している。たるみのないバンジーコードでつながれた二人(A,B)が円の上をそれぞれ p、ｑ の速度で歩いて行くとする。
バンジーコードには目印として明るいランプが取り付けてある。その位置を Q とする。
Qの位置を BQ/AB = k のパラメターであらわすことにする。 しかも Q は A B、の間だけでなく A,Bの延長線上の
任意の点に設定する ことが出来ると仮定する。（これは ｋ が 負の値も取れることを意味する。）
ｔ 時間経過したときの Q(x, y) の位置は一般に次のようにあらわされる。
x = k cos(pt) + (1 - k) cos(qt) y = k sin(pt) + (1 - k) sin(qt)このモデルを使うと エピサイクロイド 、ハイポサイクロイドの両方が同じアルゴリズムで描ける。
二次元 の 場合
| 2d_model_cardioid.dwg 2d_model_cardioid.jpg Cardioid Model ハート形-Cardioid のアニメーション  |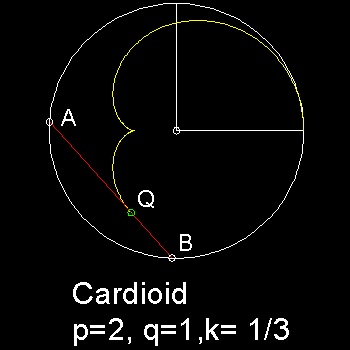
2d_model_deltoid.dwg 2d_model_deltoid.jpg Deltoid Model デルトイド-Deltoid のアニメーション  |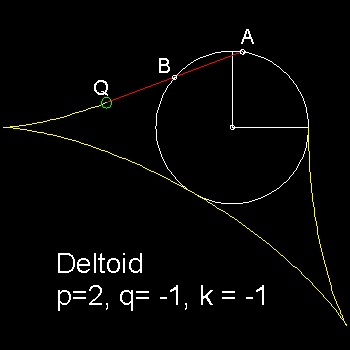
この図面の作成方法 :
プログラム generalized_trochoid.lsp をロードする。 (load "generalized_trochoid")
2 D case
コマンド ラインから 2d_model と実行命令をタイプする。
(入力データ)
Epicycloid Case:
cardioid: 2 1 1/3
nephroid: 3 1 1/4
cremona : 4 1 1/5
4 cusps : 5 1 1/6
Hypocycloid Case:
Deltoid : 2 -1 -1
Astroid : 3 -1 -0.5
5 stars : 4 -1 -1/3
6 stars : 5 -1 -1/4
三次元 の 場合
さらに 三次元に延長して考える。上述のシナリオでは A,B の二人は同一平面上の円周上を歩いていたが、今度は高さ(z 方向) の異なる
平面上の円周上を歩く場合を想定してみよう。 x-y平面を真上から見ている限り ２次元の場合と変わりはないが、
３次元曲面の断面として曲線が捉えられることが解かる。
| 3d_cardioid_view.dwg 3d_cardioid_view.jpg 3d Cardioid Model ハート形-Cardioid のアニメーション  |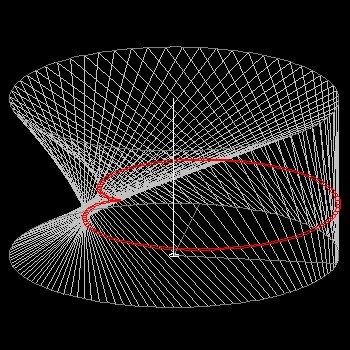
3d_deltoid_view.dwg 3d_deltoid_view.jpg 3d Deltoid Model デルトイド-Deltoid のアニメーション  |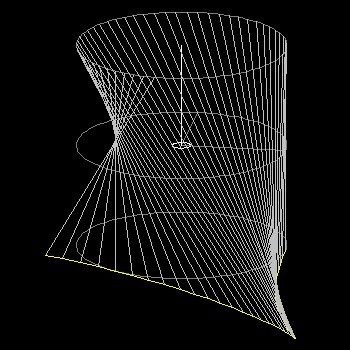
この図面の作成方法 :
プログラム generalized_trochoid.lsp をロードする。 (load "generalized_trochoid")
Cardioid case
コマンド ラインから 3d_model_view と実行命令をタイプする。
Deltoid case
コマンド ラインから 3d_model_view2 と実行命令をタイプする。
Epicycloid Case:
| 3d_cardioid.dwg 3d_cardioid.jpg Cardioid  |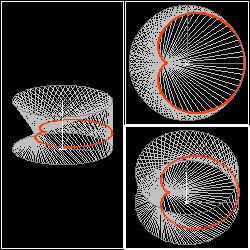
3d_nephroid.dwg 3d_nephroid.jpg Nephroid  |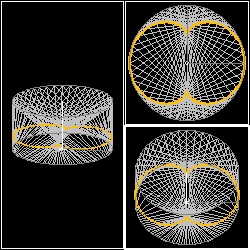
3d_cremona.dwg 3d_cremona.jpg Cremona  |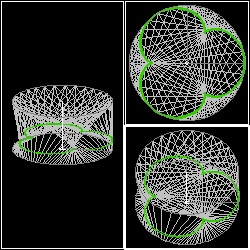
Hypocycloid Case:
| 3d_deltoid.dwg 3d_deltoid.jpg Deltoid  |
3d_astroid.dwg 3d_astroid.jpg Astroid  |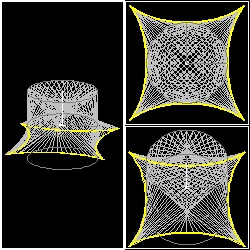
3d_5star.dwg 3d_5star.jpg 5 Star  |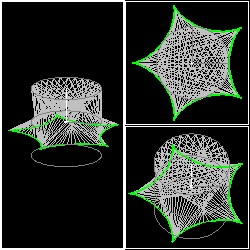
コマンド ラインから 3d_model と実行命令をタイプする。
(入力データ)
Epicycloid Case:
cardioid: 2 1 1/3
nephroid: 3 1 1/4
cremona : 4 1 1/5
4 cusps : 5 1 1/6
Hypocycloid Case:
Deltoid : 2 -1 -1
Astroid : 3 -1 -0.5
5 stars : 4 -1 -1/3
6 stars : 5 -1 -1/4
More on Epicycloid :
Case of each curve in different color:
| group_cardioid_1.dwg group_cardioid_1.jpg Deltoid  |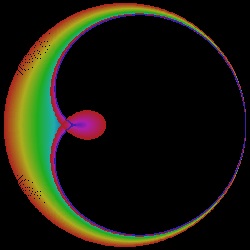
group_nephroid_1.dwg group_nephroid_1.jpg Astroid  |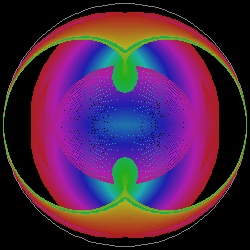
group_cremona_1.dwg group_cremona_1.jpg 5 Star  |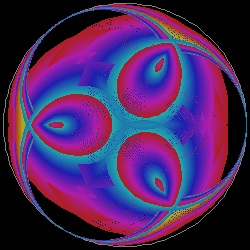
コマンド ラインから group_2dmodel_arc と実行命令をタイプする。
(入力データ)
Epicycloid Case:
cardioid: 2 1
nephroid: 3 1
cremona : 4 1
パラメター k は 0.05 - 0.85 の間を ２００ 等分して自働的に設定されている。
曲線には layer 番号が １から ２００ まで付けられてそれにより 色が変えられるように
なっている。
Case of each curve divided in 360 colors:| group_cardioid_2.dwg group_cardioid_2.jpg Deltoid  |
group_nephroid_2.dwg group_nephroid_2.jpg Astroid  |
group_cremona_2.dwg group_cremona_2.jpg 5 Star  |
コマンド ラインから group_2dmodel_arc2 と実行命令をタイプする。
(入力データ)
Epicycloid Case:
cardioid: 2 1
nephroid: 3 1
cremona : 4 1
5 star case edited using Microsoft Photo Editor
| group_5star_1.dwg group_5star_1.jpg  |
Negative - option Red group_5star_1_negativer.jpg  |
Negative - option Blue group_5star_1_negativeb.jpg  |
| Despeckle group_5star_1_despeckle.jpg  |
Water Color group_5star_1_watercolor.jpg  |
Texture- Brick option group_5star_1_brick.jpg  |
3. 直線によって出来る包絡線としての曲線
3.1 アストロイド ( Astroid )
************* string_astroid_model.dwg *************
********* string_astroid_by_line.dwg *********
*** string_astroid_model.dwg の場合：
この図面の作成方法 :
プログラム string_hypocycloid.lsp をロードする。 (load "string_hypocycloid")
コマンド ラインから string_hypocycloid_model と実行命令をタイプする。
(入力データ) 外側の円の半径= 4, 外側の円の半径= 1, に設定して、 一周を 36 分割にする。
実行終了後、 図面に修正を加える。
*** string_astroid_by_line.dwg の場合：
この図面とアニメーションの作成方法 :
プログラム string_by_line.lsp をロードする。 (load "string_by_line")
コマンド ラインから astroid_auto と実行命令をタイプする。
(入力データ) 8 分割にする。
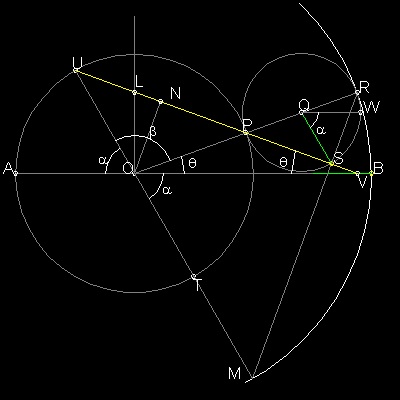
先ず LV = OR = a (外側の円の半径)であることを 説明しておく。
UV が Y軸と交わる点を L とする。
ON は UV に下ろした垂線である。
α, β , θ の間には次の関係がある。
α = { {a-b) / b } θ
β = π - (α + θ) = π - 4 θ
ΔOLV を考える。 ∠NOV = β/2 + θ = (1/2)(π - 4θ) + θ = π/2 - θ 従って ∠NVO = π/2 - ∠NOV = θ 更に ∠LOP = π/2 - θ = ∠OLP ΔOLVにおいて ΔOLP ΔOVP はいずれも 二等辺三角形である。 故に LP = OP = PV そして LV = 2 (OP) = a (外側の円の半径)
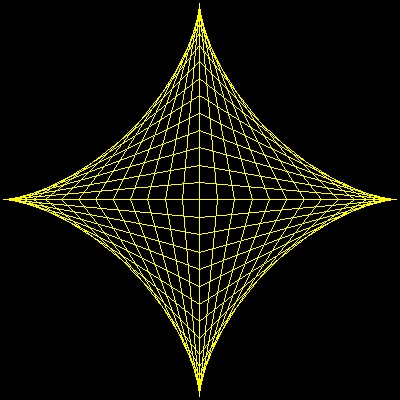
言い換えるならば 、 長さ a の棒 をそれぞれの端点が X,Y 軸上に沿って動くようにすると
その包絡線が アストロイド になる。
3.2 放物線 ( Parabola )
************** parabola_property.dwg **************
************** parabola_by_line.dwg **************
*** parabola_property.dwg の場合：
この図面の作成方法 :
プログラム parabola.lsp をロードする。 (load "parabola")
コマンド ラインから parabola_prop と実行命令をタイプする。
実行終了後、 図面に修正を加える。
*** parabola_by_line.dwg の場合：
この図面とアニメーションの作成方法 :
プログラム curve_stitch.lsp をロードする。 (load "curve_stitch")
コマンド ラインから parabola_by_line と実行命令をタイプする。
(入力データ) 10 分割にする。(既定値）
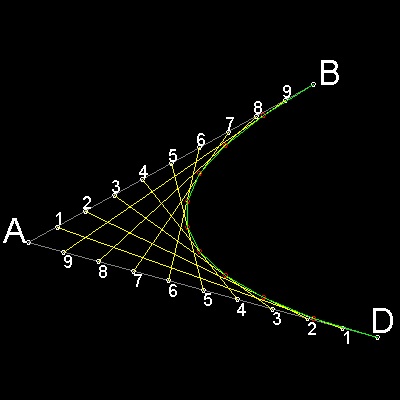
上の右の図のように ２本の直線を同じ数で等分割して その点を順序正しく線でつなぐと
包絡線として放物線が得られることはよく知られている。
包絡線が放物線であることの証明はなんと 2000年 以上も前に
アポロ二ウス(Apollonius of Perga(about 262 BC - about 190 BC) ) によってなされている。(参考 9 )
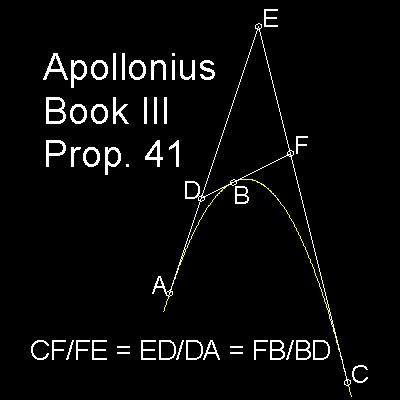
彼の著書 "Conics" の第 III 巻、には 定理 41 (Proposition 41)が次のように述べられている。
"放物線に接する３本の直線が交わるとき、それらはお互いに同じ比に分割される。"
上の図を参照のこと。
A, B, C は 放物線上の点で ADE, EFC, DBF はそれに接する直線である。
そのとき CF : FE = ED : DA = FB : BD である。
この定理の証明には 、第 I, II 巻の結果を使うので、長くなるのでここでは省略する。
(参考 3 )には簡単な説明がされているから 、興味のある人は それを参照されたい。
放物線の定義には 焦点と directrix が必要である。 この場合にそれを見つける方法がある。
そのためには(参考 3)に次のように述べてある特性を利用する。
"Three tangents to a parabola form a triangle whose orthocentre lies on the
directrix and whose circumcircle passes through the focus"
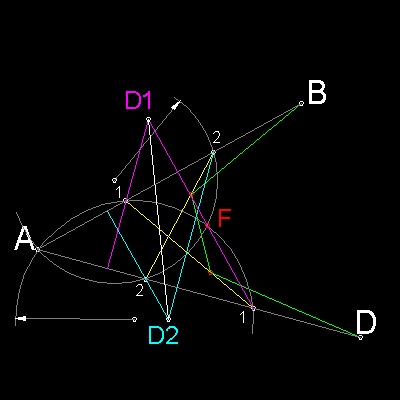焦点とdirectrix を図式的に求める方法
直線 AB, AD を三等分して上と同様な包絡線を引く。
すると 2 つの 三角形 ΔA11, ΔA22 ができる。
それぞれの外接円の交点 F が 焦点である。
2 つの 三角形のorthocenter をそれぞれD1,D2 とする。
直線D1-D2 が directrixである。
この図面の作成方法 :
プログラム curve_stitch.lsp をロードする。 (load "curve_stitch")
コマンド ラインから parabola_by_line と実行命令をタイプする。
(入力データ) 3 分割にする。
実行終了後、 図面に修正を加える。
************** parabola_focus_dx.dwg **************
(参考 5)の著者は 包絡線の方法を 放物線を描く 5 番目として説明しているが
"...確かに放物線ではあるが 焦点、その他の特性をもとめることが 困難であり、実用性に乏しい。"
と述べるにとどめている。
しかし アートの心得のある(参考 3)の著者 Jon Millington にとっては これは ストリング アート のアイデアの宝庫である。
次にその一部を紹介しておく。
ストリング アート
- 多角形 -
直感的に見て 正多角形への適用は説明を要しないと思われる。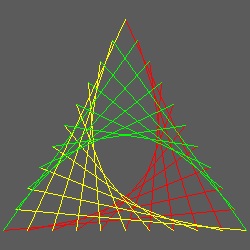
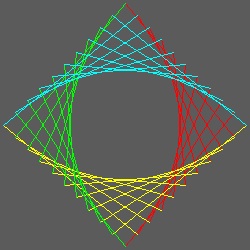
********* 3_polygon.dwg ******** ******** 4_polygon.dwg ******* ******** 5_polygon.dwg ********
この図面とアニメーションの作成方法 :
プログラム curve_stitch.lsp をロードする。 (load "curve_stitch")
コマンド ラインから polygon_demo と実行命令をタイプする。
(入力データ) 正多角形の辺の数を入力する。
- 雨の滴（しずく） -
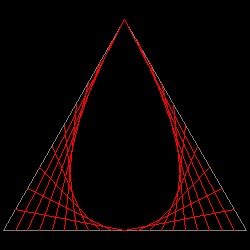正多角形の中心を頂点とする三角形を考える。底辺の半分と隣の一辺を使って放物線を描く。
後の半分についても同様な操作をする。
結果は 水滴のような面白い形になる。
参考文献[14]はこれを "raindrop"(雨の滴）となずけている。
この図面とアニメーションの作成方法 :
プログラム curve_stitch.lsp をロードする。 (load "curve_stitch")
コマンド ラインから test_raindrop と実行命令をタイプする。
****** basic_raindrop.dwg ******
このアイデアを正多角形に適用した結果を示す。
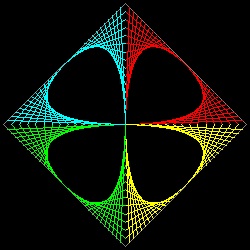
********* 3_raindrop.dwg ********
******** 4_raindrop.dwg *******
******** 5_raindrop.dwg ********
この図面とアニメーションの作成方法 :
プログラム curve_stitch.lsp をロードする。 (load "curve_stitch")
コマンド ラインから raindrop_demo と実行命令をタイプする。
(入力データ) 正多角形の辺の数を入力する。
- 星形 -
円に内接する正多角形の 半径を使って放物線を描くと面白い 星の形が得られる。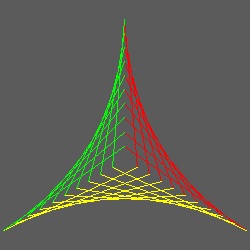
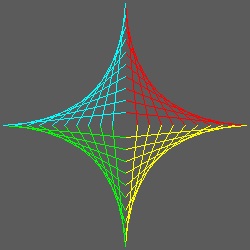
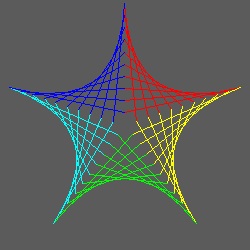
*********** 3_star.dwg ********* ********** 4_star.dwg ********* ********* 5_star.dwg **********
この図面とアニメーションの作成方法 :
プログラム curve_stitch.lsp をロードする。 (load "curve_stitch")
コマンド ラインから star_demo と実行命令をタイプする。
(入力データ) 星の角の数を入力する。
- 花びら -
直線を円弧で置き換えると 包絡線は放物線にはならないが 面白い曲線になることを使って花びら みたいな 包絡線をつくることができる。
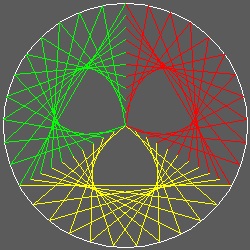
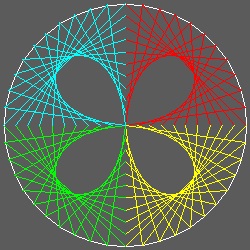
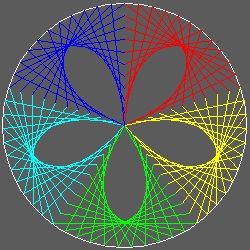
********** 3_petal.dwg ********* ********* 4_petal.dwg ********* ********* 5_petal.dwg *********
この図面とアニメーションの作成方法 :
プログラム curve_stitch.lsp をロードする。 (load "curve_stitch")
コマンド ラインから petal_demo と実行命令をタイプする。
(入力データ) 花弁の数を入力する。
- 三次元多面体への拡張 -
上述の二次元包絡線 を三次元多面体に応用すると 面白い図形を作り出すことが出来る。正四面体、正八面体、 正二十面体 の例を示す。
色々なアイデアをくみあわせると もっと多くの可能性がある。
正四面体
| tetra_1.dwg tetra_1.jpg tetra parabola  |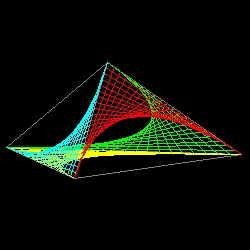
tetra_2.dwg tetra_2.jpg tetra raindrop  |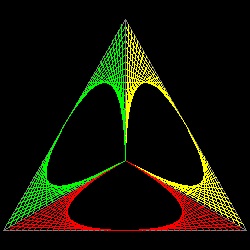
正八面体
| octa_1.dwg octa_1.jpg 8 parabolas  |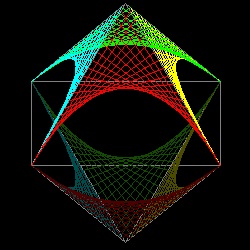
octa_2.dwg octa_2.jpg 8 raindrops  |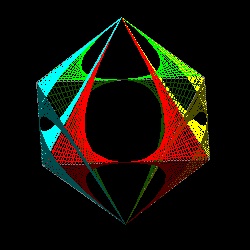
octa_3.dwg octa_3.jpg 2 footballs  |
正二十面体
| icosa1.dwg icosa1.jpg 10 parabolas  |
icosa2.dwg icosa2.jpg 20 parabolas  |
icosa3.dwg icosa3.jpg 10 parabolas #2  |
| icosa4.dwg icosa4.jpg 10 raindrops  |
icosa5.dwg icosa5.jpg 20 raindrops  |
この図面とアニメーションの作成方法 :
プログラム curve_stitch.lsp をロードする。 (load "curve_stitch")
コマンド ラインから tetra1, tetra2, octa1, octa2, octa3, icosa1, 2, 3, 4, 5 と実行命令をタイプする。
3.3 シムソン線が作るデルトイド (Deltoid by Simson line)
シムソン線は １７世紀のスコットランドの数学者 ロバート シムソン Robert Simson(1687 - 1768) が最初に見つけたとされているが 歴史家が彼の遺稿を調べてところ 何処にも 見当たらないことがわかった。
いまでは 1797年に これもまた スコットランドの数学者 ウイリアム ウォレス William Wallace( 1768 - 1843) によって
発見されたものであるとされている。 従って ウォレス-シムソン線, また 単に ウォレス線 とも呼ばれている。
シムソン は それまで はヨーロッパの数学者に ラテン語訳でしか読めなかった ユークリッド の"幾何学原論"
の英語訳を初めて出版したことで有名である。 それ以後 "幾何学原論" はアメリカ, ヨーロッパで広く普及した。
ロバート シムソン と言えば "幾何学原論" というほど 有名であったことから 彼の死後に或る数学者
が 誤って シムソン線と名前をつけても 誰も疑うことはなかったと思われる。
シムソン線
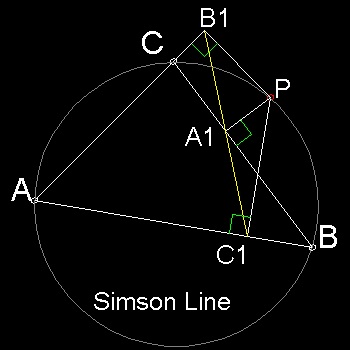
Δ ABCの外接円周上の点 P から BC, CA, AB に下ろした垂線の足をそれぞれ A1,B1,C1とすると
三点 A1,B1,C1 は一直線上にある。（この直線をP のシムソン線という。） (下の左図)(参考 XXX )
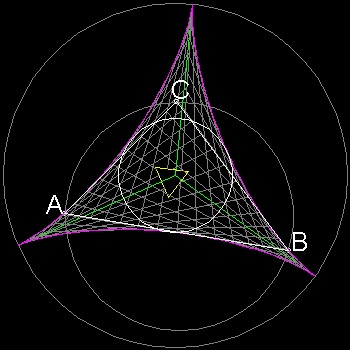
シムソン線は幾つかの面白い特性を持っている。 その中で最も驚くべきことは 点P が円周を一回りするとき
そのシムソン線の包絡線が デルトイド (Deltoid)になることである。 (下の右図)
これについては ( ) にスタイネル
Jakob Steiner (1796 - 1863)
による証明が述べられている。
その理由で デルトイド のことを スタイネル のハイポサイクロイド(Steiner's Hypocycloid) と呼ぶ人もいる。
************** Simson_line.dwg **************
********** deltoid_by_Simson.dwg **********
この図面の作成方法 :
プログラム envelop_by_line.lsp をロードする。 (load "envelop_by_line")
コマンド ラインから simson_test1, simson_test2 と実行命令をタイプする。
実行終了後、 図面に修正を加える。
シムソン線の包絡線を綺麗に描くにはシムソン線とデルトイドの関係を利用することが必要である。 それは
1. デルトイドに内接する円は ΔABC の九点円である。
九点円を簡単に描くには 三辺の中点を通る円を作ればよい。九点円については (参考 )を参照されたい。
2. デルトイドのカスプの方向はΔABC の内部に作った モーリーの三角形(Morley's Triangle)の方向と一致する。
モーリーの三角形 はケンブリッジ大学で数学を学んだ後 アメリカに移住して アメリカの数学界に大きな貢献をした
フランク モーリーFrank Morley(1860 - 1937)
による モーリーの定理 (Morley's Theorem)で定義される正三角形のことである。
モーリーの定理 (Morley's Theorem)
任意の三角形の内角を三等分する線をひく。各辺に近い一組の線の交点を結ぶ三角形は 正三角形である。
この定理の証明は (参考 )に述べられている。
3.4 3次元曲面 ( hyperbolic Paraboloid )
4. 円によって出来る包絡線としての曲線
固定点を通り、中心がある曲線上を動く円が作る包絡線は 垂足曲線と関係がある。詳細については 7.2 垂足曲線 (pedal curves) を参照されたい。
4.1 リマソン ( limaçon )
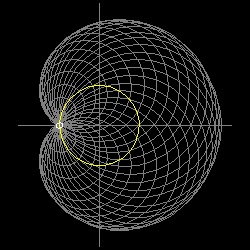
半径がa の円を描く。 X 軸上に固定点 A を決める。 中心 Qがこの円周上にあり AQを半径とする円を数多く描くと,その包絡線は リマソン ( limaçon (かたつむり）)と呼ばれる曲線になる。
点 A の位置が 円の外側、円周上、円の内側 の何処にあるかによって 異なる形になる。
特に 点 A が 円周上にある場合は 良く知られた Cardioid になる。
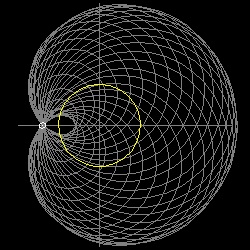
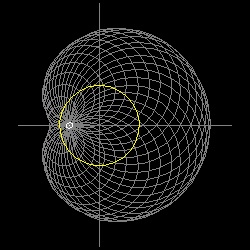
********* limason_1.dwg ******** ******** limason_2.dwg ******** ******** limason_3.dwg ********
この図面とアニメーションの作成方法 :
プログラム envelop_by_circle.lsp をロードする。 (load "envelop_by_circle")
コマンド ラインから limason_by_circle_1, 2, 3 と実行命令をタイプする。
4.2 エピサイクロイド(Epicycloid)
上の最初の曲線は じつはエピサイクロイドの仲間で Cardioid と呼ばれているものである。中心が基準円上にあって 直径に接する円を描くとその包絡線が Nephroid になることが知られている。
円が固定点を通るのが Cardioid, 直径に接するのが Nephroid... となっている。
これを拡張すると 内接する正多角形の一辺に接し、中心が 基準円に上にある円による包絡線が
一般にエピサイクロイドになると考えるのは自然であろう。
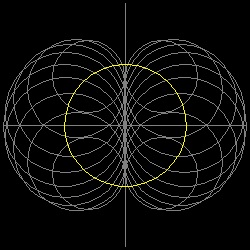
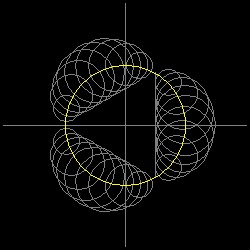
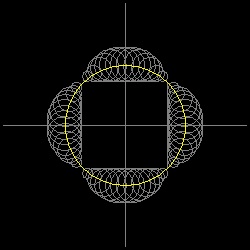
**** nephroid_by_circle.dwg ***** ***** cremona_by_circle.dwg **** ***** 4cusp_by_circle.dwg *****
この図面とアニメーションの作成方法 :
プログラム envelop_by_circle.lsp をロードする。 (load "envelop_by_circle")
コマンド ラインから epicycloid_by_circle と実行命令をタイプする。
(入力データ) 突起の数を入力する。 (2 , 3 , 4 ...)
円錐曲線上を動く円の作る包絡線
中心が円錐曲線上にあり 固定点を通る円は面白い形をした 包絡線をつくる。直角双曲線 --- レム二スケート ( lemniscate )
その中心が双曲線上にあり、座標原点を通る円の包絡線はレム二スケート ( lemniscate ) と呼ばれるリボンの形をした曲線になる。
正しくは "ベルヌーイの双葉曲線" (The Lemniscate of Bernoulli)と呼ばれるこの曲線の名前は 1694年 に
Jacques Bernoulli (1654 - 1705)が発表した論文の中で "... 数字の 8 ,もしくはリボンの蝶結び" に似た形をしているので
ラテン語の lemniscus (勝利者の花輪につけるウールのリボン) という言葉を使ったことに由来している。
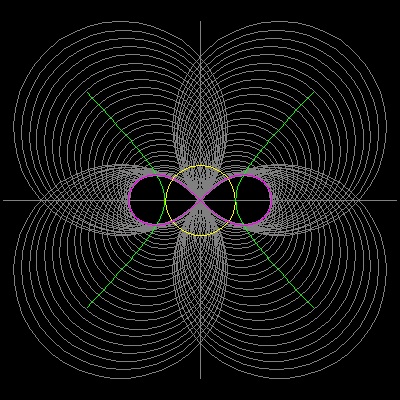
直角双曲線 x2 - y2 = c2 上の点 T(a,b)を中心とし 中心点 (0,0) を通る円は f(x,y,a,b) = x2 -2ax + y2 - 2by = 0 (1) a2 - b2 = c2 なる関係を使うと この式は f(x,y,a) = x2 - 2ax + y2 - 2y(a2 - c2)1/2 = 0 (2) となる。 包絡線は ∂f/∂a = 0 を満足するから ∂f/∂a = -2x -2ay/(a2 - c2)1/2 = 0 (3) これから次の関係が得られる。 a2(x2- y2) = c2x2 (4) (4)を (2)に代入して パラメター a を消去すると (x2 + y2)2 = c2(x2 - y2) (5) 極座標表示をすると r2 = c2cos2θ (6) ここで r = (x2 + y2)1/2 cosθ = x/r; sinθ = y/r である。 (5),(6) 式が "ベルヌーイの双葉曲線" である。
************ leminiscate_by_circle.dwg ************
この図面とアニメーションの作成方法 :
プログラム envelop_by_circle.lsp をロードする。 (load "envelop_by_circle")
コマンド ラインから leminiscate_by_circle と実行命令をタイプする。
放物線 --- シッソイド (Cissoid of Diocles)
正確には"デオクレスのシッソイド" (cissoid of Diocles)と呼ぶべきこの曲線はデオクレスが立方体の倍積問題を解くために発明したものである。
その語源は ギリシャ語の kissos (つた 蔦 )である。 カスプ の形がつたの葉に似ていたからだと言われている。
現在では シッソイド は垂足曲線などと同じく曲線を作り出す一手法として解釈されているので "----のシッソイド" の形式で使われている。
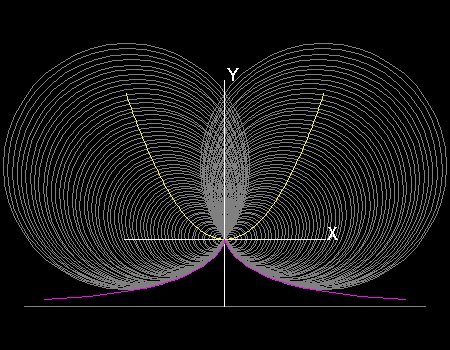
直角双曲線 x2 = 4 k y 上の点 T(a,b)を中心とし 中心点 (0,0) を通る円は f(x,y,a,b) = x2 -2ax + y2 - 2by = 0 (1) a2 = 4kb なる関係を使うと この式は f(x,y,a) = x2 - 2ax + y2 - (y/2k)a2 = 0 (2) となる。 包絡線は ∂f/∂a = 0 を満足するから ∂f/∂a = -2x -(a/k)y = 0 (3) これから次の関係が得られる。 a = -2k(x/y) (4) (4)を (2)に代入して パラメター a を消去すると x2 y + 2k x2/y + y2 = 0 (5) (5) に y を乗じる と x2(y + 2k) + y3 = 0 書き換えると x2 = - y3/(y + 2k) (6) 極座標表示をすると r = -2k(cosθ)2/sinθ (7) ここで r = (x2 + y2)1/2 cosθ = x/r; sinθ = y/r である。 (6),(7) 式が "デオクレスのシッソイド" である。
****************** cissoid_by_circle.dwg ******************
この図面とアニメーションの作成方法 :
プログラム envelop_by_circle.lsp をロードする。 (load "envelop_by_circle")
コマンド ラインから cissoid_by_circle_x と実行命令をタイプする。
5. 楕円によって出来る包絡線としての曲線
5.1 双曲線 ( Hyperbola )
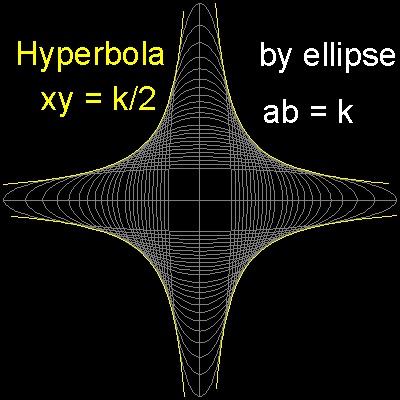
楕円群: (x/a)2 + (y/b)2 = 1 a x b = k (const) これから (x2/a3)da + (y2/b3)db = 0 b.da + a.db = 0 ここで (x2/a3) = λb , (y2/b3) = λa とおくと 微分によってえられた両式は同値になる。そして 最初の式に a をかけて、次式にｂをかけて、加え会わせると 1 = 2λab = 2λk 従って λ = (1/2k) (xy)2 = (k/2)2 即ち xy = k/2 これは 双曲線である。
この図面とアニメーションの作成方法 :
プログラム envelop_by_ellipse.lsp をロードする。
(load "envelop_by_ellipse")
コマンド ラインから hyperbola_by_ellipse と実行命令をタイプする。
************ hyperbola_by_ellipse.dwg ************
5.2 アストロイド ( Astroid )
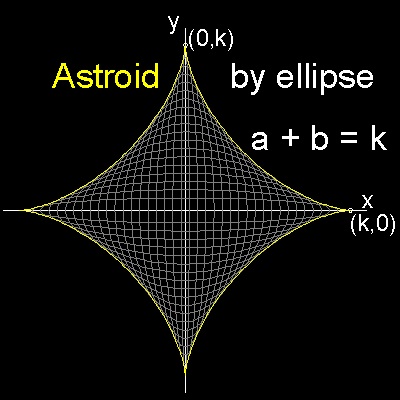
楕円群: (x/a)2 + (y/b)2 = 1 a + b = k (const) これから (x2/a3)da + (y2/b3)db = 0 da + db = 0 ここで (x2/a3) = λ , (y2/b3) = λ とおくと 微分によってえられた両式は同値になる。そして 最初の式に a をかけて、次式にｂをかけて、加え会わせると (x/a)2 + (y/b)2 = 1 = λ(a + b) = λk 従って λ = 1/k x2/3 = (a3λ)1/3 = aλ1/3 y2/3 = (b3λ)1/3 = bλ1/3 であるから 加え合わせると x2/3 + y2/3 = (a + b)λ1/3 = k(1/k)1/3 = k2/3 これは アストロイド ( Astroid ) である。
この図面とアニメーションの作成方法 :
プログラム envelop_by_ellipse.lsp をロードする。
(load "envelop_by_ellipse")
コマンド ラインから astroid_by_ellipse と実行命令をタイプする。
************ astroid_by_ellipse.dwg ************
6. 放物線によって出来る包絡線としての曲線
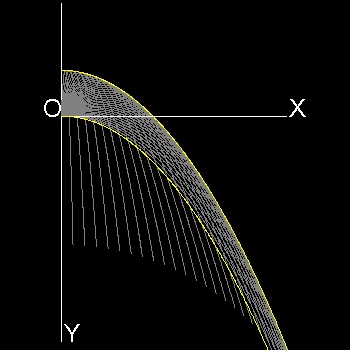
水平から 傾き角度 θ で銃弾を初速 V0 で発射すると それは 放物線を描くことが知られている。では 角度を 0 から 90 度 まで 変えたとき その包絡線はどうなるのであろうか。
その答えは 発射点を高くして 水平に発射したときの 放物線 と同じ形になる。
この問題は Fatio de Duillier が出した問題で John Bernoulli によって解かれた。
これが 包絡線として歴史上 初めて求められた例である。(参考 12)
6.1 放物線 ( Parabola )
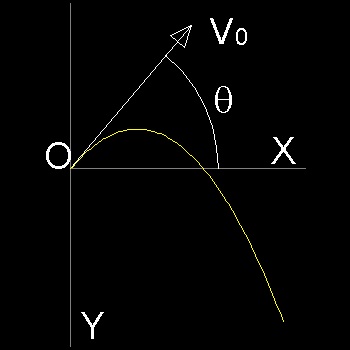
************ trajectory_desc.dwg ************
******** envelop_by_parabola.dwg *********
この図面の作成方法 :
プログラム trajectory.lsp をロードする。 (load "trajectory")
コマンド ラインから epicycloid_model と実行命令をタイプする。
(入力データ) 内側の円の半径= 1, 外側の円の半径= 1, に設定して、 一周を 72 分割にする。
実行終了後、 図面に修正を加える。
x,y 方向の初速は それぞれ V0cosθ , V0sinθ であるから 時間 t が経過した時点での 速度成分を Vx, Vy とすると Vx = dx/dt = V0cosθ (1) Vy = dy/dt = -V0sinθ + gt (2) である。ここで g は 重力加速度 である。 発射後、t 時間 経過した時点での x,y は (1),(2)を 時間積分すると得られる。 x = V0cosθ t (3) y = -V0sinθ t + (g/2)t2 (4) この式を使うと 時間 t をパラメターとして x-y 平面上に 放物線が描かれる。 包絡線を 見つけるためには このパラメター t を取り除く必要がある。 そのためには (3) から得られる t = x/(V0cosθ) (5) を (4) に代入して y を x の関数として表す。 y = -(tanθ)x + (g/2)(x/V0cosθ)2 (6) 書き換えると f(x,y) = y + tanθ - (g/2)(x/V0cosθ)2 (7) 包絡線を求めるために ∂f/∂θ = 0 と 置くと ∂f/∂θ = 1 - (g x tanθ )/(V0)2 = 0 (8) これから (tanθ) x = (V0)2/g (9) これを (6)に代入して 1/(cosθ)2 = 1 + (tanθ)2 なる等式を使うと y = -(1/2g)(V0)2 + (g/2)(x/V0)2 (10) が得られる。 これが 求める 包絡線である。 つまり この包絡線は -(1/2g)(V0)2 の高さから 水平に発射したときに銃弾の描く 放物線である。 -(1/2g)(V0)2 は θ=90 度 の時上昇出来る最大の高度である。
7. 包絡線,垂足曲線 について
7.1 包絡線 (envelope)
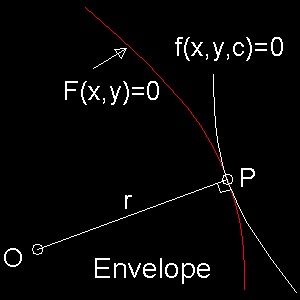
パラメター c を含む曲線群 f(x,y,c) = 0 が 曲線 F(x,y) = 0 と 一点を共有し、しかも その点で F(x,y) = 0 の曲率半径 OP と直交する(つまり 接線を共有する）とき
F(x,y) = 0 は f(x,y,c) = 0 の包絡線であると言う。数学的には次のように定義される。
パラメター c を含む曲線群
f(x,y,c) = 0 (1) が与えられたとき (∂f/∂c) = 0 (2) を使って (1) から パラメター c を消去して得られる F(x,y) = 0 (3) が包絡線である。 パラメター が二個(a,b)ある場合： 曲線群 : f(x,y,a,b) = 0 パラメターの条件: g(a,b) = 0 f と g を a, b で偏微分して (∂f/∂a)da + (∂f/∂b)db = 0 および (∂g/∂a)da + (∂g/∂b)db = 0 これらを同時に満足するには (∂f/∂a) = λ(∂g/∂a) (∂f/∂b) = λ(∂g/∂b) でなければならない。この関係を使って a,b を消去すれば 包絡線 F(x,y) = 0 が得られる。 ここで λ は未定の定数である。以下に例題を使って説明する。
********** envelope_def.dwg **********
包絡線を見つける方法の例(1)
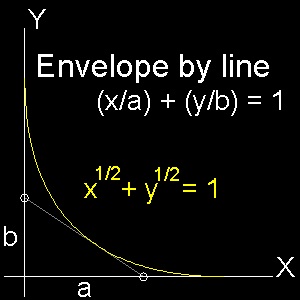
直線群 : x/a + y/b = 1 a + b = k (const) これから (x/a2)da + (y/b2)db = 0 da + db = 0 ここで x/a2 = λ2 , y/b2 = λ2 とおくと 微分によってえられた両式は同値になる。そして √x + √y = aλ + bλ = λ = const がパラメター a,b を消去した結果となる。 これは 放物線である。
********** env_by_line_def.dwg **********
この図面の作成方法 :
プログラム envelop_by_line.lsp をロードする。 (load "envelop_by_line")
コマンド ラインから parabola_by_line と実行命令をタイプする。
結果の図に変更を加える。
包絡線を見つける方法の例(2)
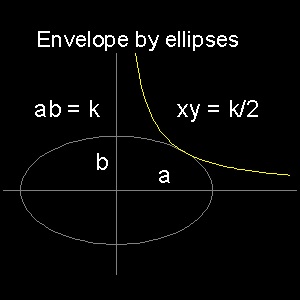
楕円群: (x/a)2 + (y/b)2 = 1 a x b = k (const) これから (x2/a3)da + (y2/b3)db = 0 b.da + a.db = 0 ここで (x2/a3) = λb , (y2/b3) = λa とおくと 微分によってえられた両式は同値になる。そして 最初の式に a をかけて、次式にｂをかけて、加え会わせると 1 = 2λab = 2λk 従って λ = (1/2k) (xy)2 = (k/2)2 即ち xy = k/2 これは 双曲線である。
******* env_by_ellipse_def.dwg *******
この図面の作成方法 :
プログラム envelop_by_ellipse.lsp をロードする。 (load "envelop_by_ellipse")
コマンド ラインから hyperbola_by_ellipse と実行命令をタイプする。
結果の図に変更を加える。
包絡線を見つける方法の例(3)
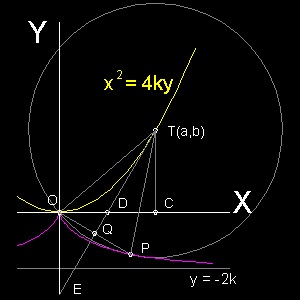
放物線 x2 = 4ky 上の点 T(a,b) を中心として 原点 (0,0) を通る 円群の 包絡線 を見つける。 円の方程式は : f(x,y,a) = x2 - 2ax + y2 - (y/2k)a2 = 0 これを a で微分すると ∂f/∂a = -2x -ay/k = 0 これから a = -2k(x/y) これを 円の方程式に代入すると 次の様な結果になる。 x2y + 2kx2 + y3 = 0 書き換えると x2 = - y3/(y + 2k) 点 P の軌跡は y = -2k を漸近線とする デオクレス のシッソイド (cissoid of Diocles)である。 点 Q は 接線 ET 上に下ろした 垂線 との交点である。 このような 点Q の軌跡 は 垂足曲線 (pedal curves) と呼ばれている。 OQ = QP なる関係があるので Q もまた 別のシッソイド 上にある。 その曲線の式は x2 = - y3/(y + k) である。
****** cissoid_by_circle_desc.dwg ******
この図面の作成方法 :
プログラム envelop_by_circle.lsp をロードする。 (load "envelop_by_circle")
コマンド ラインから cissoid_by_circle_x と実行命令をタイプする。
結果の図に変更を加える。
7.2 垂足曲線 (pedal curves)
(参考 10) に非常に解かり易い説明があるのでそれを使わせてもらう。例題には 垂足曲線 と円による包絡線の関係を示すために x2 = 4ky の形の放物線を選んだ。
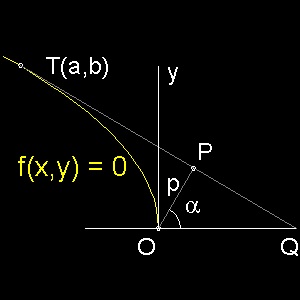
あたえられた 曲線 f(x,y) = 0 (1) 上の点 T(a,b)における 接線は (x - a)(∂f/∂x)a + (y - b)(∂f/∂y)b = 0 (2) ここで (∂f/∂x)a (∂f/∂y)b は それぞれ (∂f/∂x) (∂f/∂y) の 点T での値である。 簡単に それぞれ fa, fb と書くことにする。 また 一般の直線は極座標表示では x cosα + y sin α - p = 0 (3) ２式 (2),(3)が同一の直線であるための条件は fa / cosα = fb / sin α = (a fa + b fb)/ p (4) 上の ２式 (1),(4) から 二個のパラメター a,b を消去した関係式が 点 P の軌跡を表すことになる。
この図面の作成方法 :
cissoid_by_circle_desc.dwg を９０度回転したあと 修正を加える。
******** pedal_curve_desc.dwg ********
垂足曲線を見つける方法の例(1)
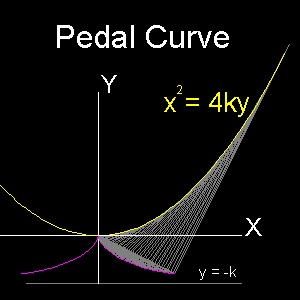
放物線 x2 = 4ky に対して 原点(0,0) を極とする 垂足曲線 を見つける。 f(x,y) = x2 - 4ky = 0 T(a,b) における fa, fa の値は fa = 2a fa = -4k 従って 上の (4) 式は次のようになる。 2a/cosα = -4k/sinα = a2 / p これから cosα = 2p/a , sinα = -4kp/a2 cosα , sinα を使って パラメター a を消去する。 (cosα)2/ sinα = - p/k 書き替えると p = -k(cosα)2/ sinα これは デオクレス のシッソイド (cissoid of Diocles)である。 直交座標を使うと x2 = - y3/(y + k) となる。
****** cissoid_by_pedal.dwg ******
この図面の作成方法 :
プログラム curve_by_pedal.lsp をロードする。 (load "curve_by_pedal")
コマンド ラインから cissoid_by_pedal_x と実行命令をタイプする。
References
- Yates, Robert C.: A Handbook on Curves and their Properties. J.W.Edwards,1947.
- Lockwood,E.H.: A Book of Curves. Cambridge University Press, First edition published in 1961 .
- Millington, Jon: Curve Stitching. Tarquin Publications.1989.
- Downs, J.D.: Practical Conic Sections.-The geometric properties of ellipses,parabolas and hyperbolas. Dovers. First edition published in 1931.
- Kendig,Keith: Conics, Mathematical Association of America, 2005.
- Salmon, George: A Treatise on Conic Sections. Chelsea Publishing Company. Reprint. Original published in 1900.
- Hilbert,D.,Cohen-Vossen S.: Geometry and Imagination. Chelsea Publishing Company, English Translation. Original was published in 1932.
- Cohen,Abraham: An Elementary Treatise on Differential Equations. D.C.Heath & Co., 1933. pp86-100
- Apollonius of Perga: Conics, Book I - III,Green Lion Press,Santa Fe, NM. 1997. English Translation
- Struik,Dirk D.: Lectures on Classical Differential Geometry, Addison-Wesley press,1950. p.168
- Dörrie,Heinrich: 100 Great Problems of Elementary Mathematics, Dover,1965. English translation
- Coxeter,H.S.M., Greitzer,S.L.: Geometry Revisited, MAA,1967.
- Hornsberger,Ross: Episodes in Nineteenth and twentieth Century Euclidean Geometry,MAA.1995
- Coxeter,H.S.M.: Introduction to Geometry: 2nd Edition,John Wiley,1980.
- 佃 勉 : カーブス。 , 現代工学社, ISBN 4-87472-189-3, 1998
- 数学教育協議会/銀林 浩(編) : 折り紙算数: 折り紙数学. 数学教室,別冊 3, 国土社, ISBN 4-337-47828-0. 1994
- 安藤 清、 佐藤 敏明 : 初等幾何学， 森北出版、 ISBN4-627-03540-3, 1994
- 宇沢 弘文 : 代数で幾何を解く 好きになる数学入門 #3, 岩波書店, ISBN 4-00-006673-0, 1998
- Simonson,Andrew J.: Hesiod's Anvil--Falling and Spinning through Heaven and Earth,MAA,2007.