Ellipse case--Isochrones, Isoclinal Trajectries
List of animations posted on this page.(Click the text to watch animation.)Start from a point on the ellipse - 1
Start from a point on the ellipse - 2
This is the case when the Pursuer starts from a point on a given ellipse and the pursued travels from one of the Ellipse's foci to the center of the ellipse. The relative speed is set as a/c where a is the major axis radius, and c is the distance from the origin to one of the foci.
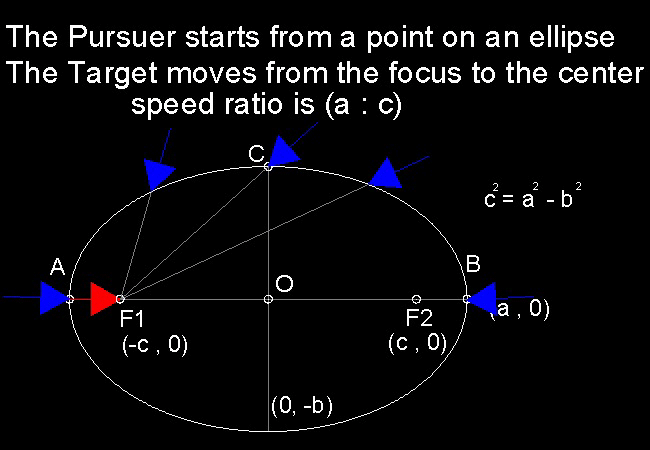
*********************** pursuit_ellipse_desc.dwg ***********************
It looks obvious that if the pursuer starts from point "A" (-a , 0) or "B" (a , 0) at the speed equal to the
multiple of (a/c) relative to the speed of the Target starting toward the origin at the same time, the pursuer
will catch up with the Target at the origin "O".
But guess what will happen when the Pursuer
begins the chase from other points on the same ellipse .
Here is the case when the Pursuer starts from point "C" (0, b).
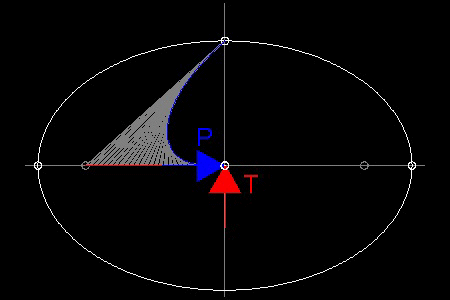
See this process in animation.
To create this drawing and animation:
Load pursuit.lsp (load "pursuit")
Then from command line, type pursuit_ellipse
********* pursuit_ellipse_1_end1.dwg *********
Surprised ? Maybe the point seleced is a special point. Let us try another point on the ellipse.
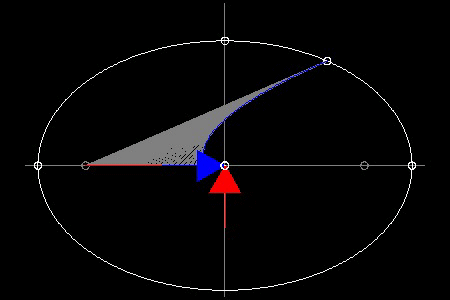
Another example animation.
To create this drawing and animation:
Load pursuit.lsp (load "pursuit")
Then from command line, type pursuit_ellipse
********* pursuit_ellipse_2_end.dwg *********
Now you must be thinking " This is not a coincidence. Maybe if the pursuer starts from any points
on the ellipse, it will always catch up with the prey at the coordinate origin (0 0)".
And your guessed it right as will be shown in the next section.
It can be stated as follows:
If P starts anywhere on the ellipse,and T starts from a focus of this ellipse,then P always captures T
at the same point,the center of the ellipse.
These curves are called "Isoclinal Trajectories"(Iso-->same, clinal-->inclination).
In the figure below, point symbols along the trajectories show the position of "P" every 20 line segments ,which can be interpreted as 20 unit time periods.
Using point data on line AB to compute the scale factor for the major axis, ellipses can be drawn. It is interesting to see that all these "equal time" points lie on each ellipse.
These ellipses are called "Isochrones ellipses"(iso-->same , chrones -->time) .
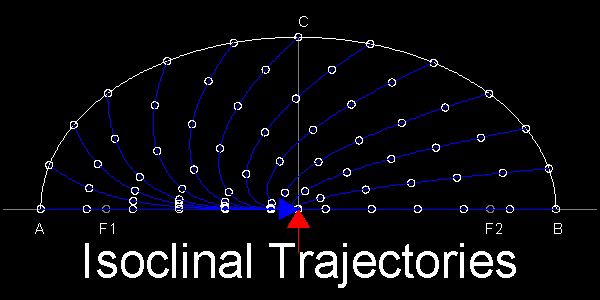
*********************** ellipse_isoclinal.dwg ***********************
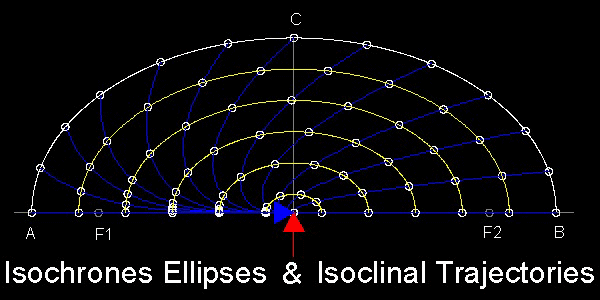
********************* ellipse_isochrones.dwg *********************
One more interesing observation:
These trajectories are made up of very short line segments. When the line segments passing through each ellipse is extended ,they will intersect line AB. The point of intersection is the focus point of the ellipse. It was shown in the next figure.
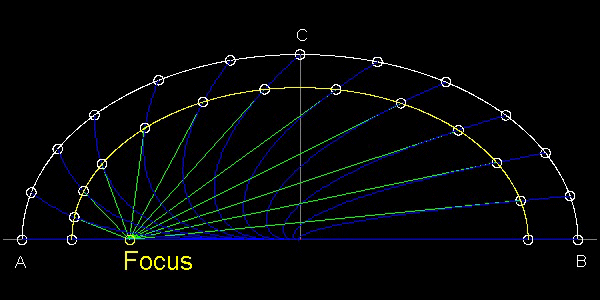
*
********************* ellipse_isochrones.dwg ********************
Mathematical background
Mathematical formulation is very similar to the Linear Motion case,
i.e.The case of the pursued running on a straight line
The difference is that now Target moves up and down the y-axis ( x=0 line ) and the Pursuer starts chasing
from an arbitrary point on the ellipse.(See the figure below)
To create this drawing and animation:
Load pursuit.lsp (load "pursuit")
Then from command line, type pursuit_ellipse