Linear Motion Case
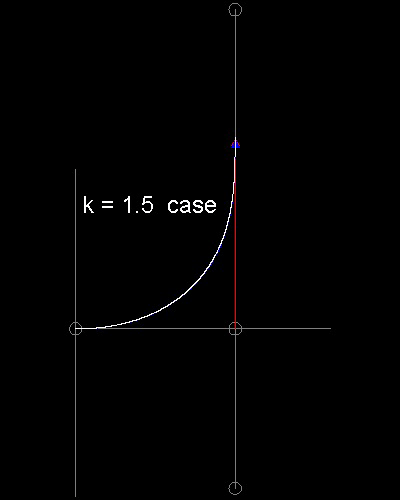
List of animations posted on this page.(Click the text to watch animation.)Linear chase -- k = 1.5 case
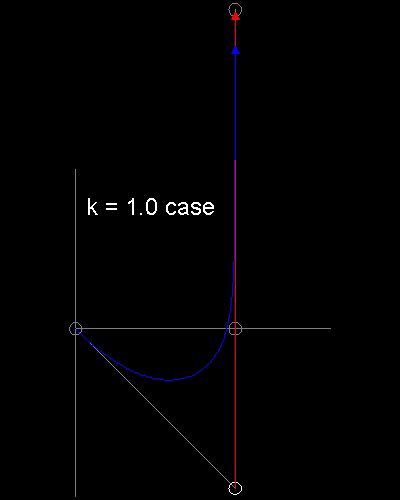
Linear chase -- k = 1.0 case
This is the case when the Pursued moves straight on a line.Let the rabbit pursued travel from rest at the
x-axis along the line x = a (figure below).The pursuing dog starts at the same time from the origin with
velocity k times the former.
Then
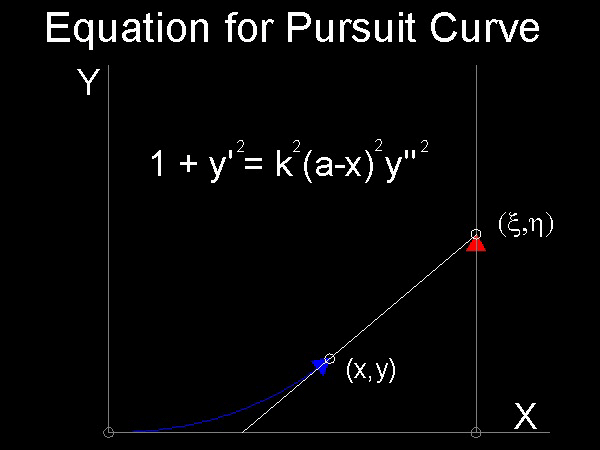
x = a, (h - y)/(a - x) = y' or h = y + (a - x)y'
dx2 + dy2 = k2(dx2 + dh2) = k2 dh2
There follows: dx2 + dy2 = k2*[dy - y'dx +(a-x)dy']2
= k2(a-x)2(dy')2
or 1 + y'2 = k2(a-x)2y''2
This is a type of differential equation solvable by first setting y ' = p. (see ref. 2, 4 & 5)
****************** pursuit_curve_equation.dwg *******************
Example output
********** linear_pursuit_1.dwg *********** ********** linear_pursuit_2.dwg ***********
See the process k = 1.5 case animation. and k = 1.0 case animation.
To create this drawing and animation :Load pursuit.lsp (load "pursuit")
from command line, type pursuit_linear
for k=1.5 case, set k=1.5, and other inputs are default values.
for k=1.0 case, start point for a rabbit is (5,-5)
Note* : This program requires red_arrow.dwg & blue_arrow.dwg .
For the case when the values of k vary from 1.01 to 3.0
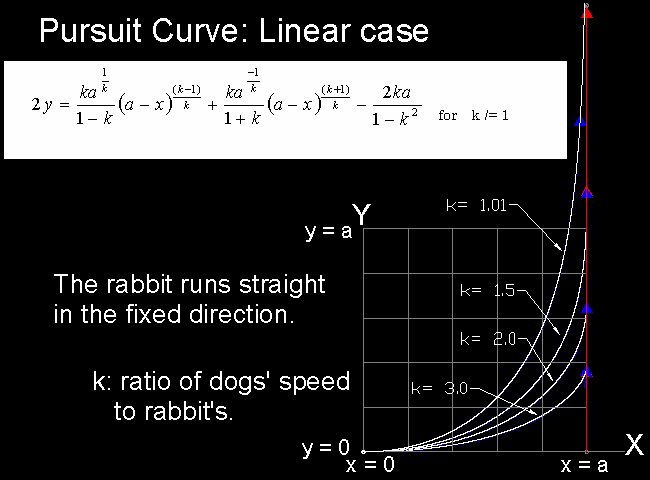
************************** pursuit_linear_1.dwg **************************
More note on the pursuit.lsp
Input defaults are set such that a rabbit starts from the point (5 , 0), and the dog will start chasing from the
point (0 , 0). The relative speed's default is set as 2.0.
This executable has the basic functions which can be used for a generic curve pursuit problem, and both the
case when the rabbit runs on the circle ( The case of the pursued running on a fixed circle ), and the case
when the dog starts from points on the ellipse and the rabbit starts from one of the focus points of the ellipse
toward the origin of the ellipse ( The case of the pursuer starting from a point on a given ellipse ) have been
developed using this as a template.